1. 引言
现实世界中,社会经济现象总是在不断的变化与发展的。当社会经济变化的长期趋势呈现出稳定的线性趋势时,可以使用移动平移法、指数平滑法、直线趋势方程拟合法对其进行预测研究。当社会经济变化的长期趋势不是线性时,但又呈现一定规律,就需要配合适当的非线性趋势曲线。比如抛物曲线型、指数曲线型、修正曲线指数型、龚珀兹曲线型等。对于长期趋势,若按照大体相同的增长速度递增或递减时,可以采用指数曲线模型或修正指数曲线模型来进行研究。
唐五湘 [1] 利用两步最小二乘法研究了指数曲线模型的参数估计,并以我国长途电话去话张数为例进行了数值计算。白雪梅和赵松山 [2] 分析了传统指数曲线模型参数估计存在的问题、适用条件并提出了改进方法和非线性近似估计法。杨佳元 [3] 根据指数曲线模型的特点,对指数曲线模型的假设、参数估计、拟合误差以及无偏性等问题进行了讨论。毛艺萍和王斌会 [4] 利用时间序列相邻两项之差建立回归方程,并用最小二乘法对模型参数进行估计。秦尚林等人 [5] 利用指数曲线模型并结合武广铁路客运专线部分实测资料讨论了路基沉降问题。张军等人 [6] 等人提出了修正指数曲线模型参数估计的一种新方法,并经过数据实验证明了参数估计新方法的有效性和实用性。欧阳明等人 [7] 在现有模型的基础上构造了一个新的修正的指数曲线模型。通过对不同类型的单桩静载荷试验数据进行拟合,验证了提出的新模型能够很好的对单桩P-S曲线进行拟合。陈希鸣等人 [8] 针对灰色GM(1, 1)模型和指数曲线模型在高速公路沉降预测中的不足,采用不等权系数将二者形成组合模型预测沉降,从而达到提高沉降预测精度的目的。
本文在上述研究的基础上,提出了时间幂次项的指数曲线以及它的参数估计方法,并将其应用于西藏自治区水资源总量中。选择西藏自治区水资源总量的研究,主要是因为西藏自治区水资源总量是我国最丰富的地方,人均占水量和亩均占有量均居全国首位。对西藏自治区水资源总量的研究就显得格外重要。本文涉及到的数据是从中国统计年鉴上获得的,其中2004年至2015年的实际数据作为建模数据,2016年至2017年的数据为模型的外推预测检验数据。对比分析指数曲线、修正的指数曲线以及本文提出的新型指数曲线,计算结果显示本文的指数曲线模型预测精度高于其它两个模型。
2. 指数曲线和修正的指数曲线
2.1. 指数曲线
由文献 [9],经典的指数曲线为
。 (1)
为了估计参数
,一般将(1)式两端取对数,得到
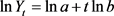 。 (2)
。 (2)
然后运用最小二乘法和方程(2),得到如下方程
, (3)
估计出参数
和
,再取反对数,即可得到参数
的估计值。
2.2. 修正指数曲线
在经典指数曲线的基础上增加一个常数K,即得到修正指数曲线模型
, (4)
其中K、a、b为未知参数,
,
,
。
参数K、a、b估计的基本思想是三和法:把整个时间序列分成相等的三个数组,每个组有m项,根据趋势值Yt的三个局部总和分别等于原数列观察值Y的三个局部总和来确定三个参数。具体为:设观察值的三个局部总和分别为S1、S2、S3,得
,
,
。 (5)
由三和法得到如下方程
。 (6)
通过方程(6)解得
。 (7)
3. 改进的幂次项指数曲线模型
在上面指数模型的基础上,本文提出幂次项指数曲线,其一般方程为
, (8)
其中参数为
。相比于经典的指数曲线模型和修正的指数曲线模型,最大的一点是引入
部分以描述序列的变化趋势。但是,改进的指数曲线带有5个未知参数,且方程(8)本身为非线性函数。所以,在对参数的估计时采用的是非线性最小二乘法。
令
,
为观测值,则通过方程(8)可得到如下的非线性方程组
。 (9)
求非线性方程组(9)的最小二乘估计量
,构造如下的残差平方和最小:
, (10)
其中
,这是一个非线性无约束最优化问题。
对于上述问题,本文采用信赖域算法来求解(10)式。信赖域算法最早可以追溯到Levenberg-Marquardt方法,它不是直接求解目标函数,而是寻找一个与之近似的问题,称为信赖域子问题,然后求得该问题的极小值进而获得目标函数的最优解。其基本思想是:先给出一个目标函数的初始估计解,然后求解目标函数的近似模型,得到的解称为试探步;通过试探步可以调节下一个迭代点,并调节信赖域半径;反复求解近似模型就可以不断更新迭代点和调节信赖域半径,直到求得目标函数的最优解为止。信赖域算法在每步的迭代过程中,都是在求解信赖域子问题,而子问题的解又总是限定在一个可信赖的广义球内。关于信赖域子问题中目标函数的构造本文选取二次模型。
对于式(10)的非线性无约束优化问题,利用二次逼近,信赖域模型的目标函数一般形式可以表示为:
, (11)
于是信赖域子问题构造如下:
,(12)
其中
为目标函数的梯度,有
, (13)
xk为第k次迭代点,
为试探步,
为Hess矩阵
(14)
为信赖域半径,其要在信赖域范围内,
为Euclid范数。
求解式(10)得到校正量
后,进一步求解
, (15)
, (16)
, (17)
其中
为实际下降量,
为预测下降量,下降比率rk为下一次的迭代半径。根据比值rk的大小来判断近似程度,rk越接近1时,收敛越好,可增大rk;rk小于0时,不收敛,需要缩小半径。
4. 具体应用
为了对新型的指数曲线的预测精度进行检验,本文选用西藏自治区水资源总量实际数据来验证分析,并将计算结果与已有的指数曲线、修正的指数曲线模型的计算结果进行对比分析。本文选取西藏自治区水资源总量2004年至2017的统计数据,见表1。

Table 1. The raw data of the total water resources of tibet autonomous region (hundred million cubic meters)
表1. 西藏自治区水资源总量的统计数据(亿立方米)
为了检验模型的预测精度,根据预测值与实际值确定绝对百分误差(APE)和平均绝对百分误差(MAPE)如下。
, (18)
。 (19)
从表达式(19)可知,当
,MAPE为拟合误差,记为MAPEfit;当
,MAPE为预测误差,记为MAPEfore;当
,MAPE为总误差,记为MAPEtotal。
通过Matlab编写数值计算程序,利用2004年至2015年的数据建立三种指数曲线模型,其表达式分别为
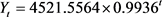 , (20)
, (20)
, (21)
。 (22)
通过表达式(20)~(22),可以计算得到相应的拟合值和预测值,具体见表2。从计算结果看出改进的指数曲线对西藏自治区水资源总量的预测更接近。指数曲线的拟合误差、预测误差和总的误差分别为4.3780%,11.6675%和5.4995%;修正的指数曲线的拟合误差、预测误差和总的误差分别为3.4466%,63.9725%和12.7583%;幂次项的指数曲线的拟合误差、预测误差和总的误差分别为9.9810%,0.8380%和8.5744%。
修正的指数曲线在拟合上是最优的,其值为3.4466%,比幂次项的指数曲线小了将近3倍。但是,幂次项的指数曲线预测误差是最低的,为0.8380%,远远小于指数曲线和修正的指数曲线的值。这说明,幂次项的指数曲线在预测上比前两种模型有更高的精度,相应的结果的可靠性也更为可靠。同时,也说明了本文提出的新型幂次项指数曲线在一定程度上是能够提高模型的预测精度的。

Table 2. The calculation results of the total water resources in Tibet autonomous region by using the exponential curve, modified exponential curve and improved exponential curve
表2. 指数曲线、修正的指数曲线和新型指数曲线对西藏自治区水资源总量的计算结果
5. 结论
本文在传统的指数曲线基础上,引入时间幂次项来描述现实世界的序列。通过非线性最小二乘法构建最优目标函数来求解模型的各个参数的取值,并进一步将其应用在西藏水资源总量的拟合预测中。从计算结果可以看出新型的指数曲线模型预测精度高于指数曲线和修正指数曲线模型。本文提出的模型在一定程度上能够提高模型的预测精度,在今后的研究中可将这种推广模型引入到如龚珀茨模型中。
NOTES
*通讯作者。