1. 引言
小波分析是这些年来发展起来的一门新兴数学理论以及方法,在信号处理,语音处理,图像处理,数据压缩,微分方程求解,地震勘探等各个领域有着广泛的应用。Haar小波是同时具有正交性,对称性和紧支撑性的单小波,但是其它单小波并不能具有这样好的性质,所以人们引入了多小波。从带宽来看,二尺度小波高频端的带宽比较窄,那么从小波分析的效果来看二尺度小波效果相对比较差,所以人们提出了a尺度小波。双向小波的概念是杨守志等人首先提出的 [1],后来进一步得出了一系列好的理论和结果 [2] [3]。本文在引入二维四向多小波基础上,建立了a尺度二维四向多加细函数和a尺度二维四向多小波,给出了a尺度二维四向多加细函数和a尺度二维四向多小波的正交和双正交准则,以及它们的构造算法,最后讨论了a尺度二维四向多小波的分解与重构的Mallat算法。
2. 预备知识
先给出文章要提到的记号:
表示N维复欧几里德空间。
表示
阶单位矩阵,
表示
阶零矩阵,
表示向量或矩阵的转置,向量值函数信号空间
可以表示为
,(根据文献 [4] )对于
它的积分和Fourier变换分别定义为
和
若F和G都是一元函数空间,它们两个的基底分别为
和
,二元函数空间H表示为
是F和G的张量积空间,H的基底可以表示为
。
定义
的张量积空间为
,而
表示为由一元尺度函数
生成的一个正交多分辨分析。那么关于二元函数
,引入记号
。
二维四向加细尺度函数
基于双向尺度函数的概念,现在假设有
个双向尺度函数
,记
,那么通过
和
的张量积来构造二维四向多尺度函数。假设双向加细函数
和
都符合细分方程
设
,就能得出
从而根据适合的
,就有
令
,则
那么就可以有a尺度多小波细分方程
(1)
接下来对(1)式进行Fourier变换就可以有
(2)
其中
令

为双正,正负和双负矩阵符号。下面对(1)进行变形有
(3)
(4)
(5)
下面对(3)~(5)式都进行Fourier变换就有
(6)
(7)
(8)
根据(2)(6)~(8)式可以有,令
(9)
方程(2)有解,当且仅当式(9)有解。
设
(10)
则(9)式为
在频域里的a尺度加密方程,它的加细面具符号为
(11)
定义方程(1)的自相关矩阵符号
其中
下面引入变换算子
:
(12)
其中
是
的Laurent多项式,
由(12)式可知。
关于
和
可以有下面的引理。
引理1:矩阵符号
和变换算子
的定义如上,那么由Poisson求和公式可得
进一步,我们可以得出
是
相应于特征值为1的特征矩阵。
定理1:加细方程(1)有紧支撑解当且仅当它的面具符号满足下面情况之一
1)
2)
3)
4)
证明:根据文献 [5] [6] [7] [8],方程(10)存在紧支撑分布解当且仅当1是(11)式定义矩阵
的一个特征值,
的其他特征值的模都不大于1。另外,
的4个特征值分别是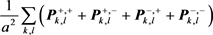 ,
,
以及
。定理易证。
,
,
以及
。定理易证。
定理2:若要
有紧支撑性,则要证明每个分量是紧支撑的。设
,其中
和
是双向细分函数满足
如果
和
是紧支撑的,那么可根据
和
的张量积生成二维四向加细函数
,
,则有
证明:根据文献 [9] 中定理4可知。
3. a尺度二维四向多分辨分析
定义子空间序列
,
(13)
那么要产生在
中的一个多分辨分析
当且仅当(13)式里的
应当满足以下条件:
1)
;
2)
;
3)
;
4)
;
5) 存在
里的一个函数
,使得集合
是
的Riesz基,那么就有两个常数
,则对于系数向量序列
有
(14)
称式(14)为稳定性条件。
根据多重多分辨分析的性质
,可以定义:
则
同样可以构成
的Riesz基,有
因为
,并且
同样也可以构成
的Riesz基,故有
,从而使
满足(1)式。
定理3:如果尺度函数
符合多分辨分析,现定义
构成
的Riesz基。若存在函数集
构成
的Riesz基,那么
。
证明:由于
构成
的Riesz基,故存在两个常数
,对任意的
,有
所以对于所有的
,就有
对于
,
,存在一个紧支撑连续函数
,使
。
若
是
的正交投影算子,则
,故
。
设
,则
其中
。所以,当
时
。同理,可以证明:
,
,
。又由于
所以
。根据
,可以知道
。
定理4:若
符合定义式(1),根据(13)式定义的
,若
满足1) 集合
是
的Riesz基;2) 对所有的
,
有界;3)
在
附近连续,
,那么
。
证明:由于
构成
的Riesz基,故存在两个常数
,对任意的
,有
所以对于所有的
,就有
对于 ,
,那么就有紧支撑连续函数
,使
。
,
,那么就有紧支撑连续函数
,使
。
若
是
的正交投影算子,则
。又因为
,则
进一步可以得到
其中
因为
,所以存在一个常数M,使
故
由以上的推导,可以得到
由于
有界且在
附近处连续且
,故当
时,以上不等式收敛于
从而
,所以
,因为
是任意小的,所以
,则说明
。
4. 双正交二维四向加细函数和小波
定理5:如果二维四向加细函数是正交的,那么应该满足下列等式
定理6:如果二维四向加细函数
和
是双正交的,那么应该满足下列等式
定理7:如果二维四向加细函数
和
是双正交的尺度函数,那么它的双正面具,正负面具和双负面具符号都应该满足
(15)
其中:
;
。
证明:由文献 [7] 的定理1以及本文定理5定理6正交双正交定义易证。
假设
和
是双正交二维四向加细函数,对任意的
,定义
,其中
是
在
中的正交补。那么当
时,就有
并且
,其中
,
,
,
。
如果有r个小波函数
,则记
,则通过张量积的构造就有
和
,使得集合
和集合
构成
的一组双正交基,则
和
是与
和
对应的双正交二维四向多小波函数,应该满足
(16)
其中:
。
假如
是
对应的多小波函数,相应的
是
对应的多小波函数,那么就存在
,
,
,
和
,
,
,
,满足
(17)
(18)
对(17)式和(18)式两边做Fourier变换
其中
为
的双正,正负,双负面具符号。
为
的双正,正负,双负面具符号。
定理8:若
和
是双正交二维四向多加细函数,
和
是相应的双正交二维四向多小波函数,则它们的面具符号满足
 (19)
(19)
 (20)
(20)
其中:
。
证明:根据(16)式的正交性易得。
5. 构造算法
定理9:如果
和
是双正交二维四向多加细函数,
和
是相应的双正交二维四向多小波函数,
和
是矩阵符号,构造
。函数
和
以
为周期,且满足
1)
2)
3)
4)
则
和
,产生一个双正交二维四向多细分函数
并满足
证明:将上面已经构造的
和
,代入(15)式化简可得。再令(11)式
,则化简
并求特征值可证得定理。
定理10:如果
和
是双正交二维四向多加细函数,
和
是相应的双正交二维四向多小波函数,
和
是面具符号,构造
。函数
,
和
以
为周期,且满足
1) 
2)