1. 概述
工字形钢一般也称为型钢梁(英文名又称为:Universal Beam) [1],如图1所示截面为工字形状的钢梁,工字形钢大致可以分为热轧工字钢和轻型工字钢,是截面形状为工字形的钢材种类,由于其自身的优点,截面形状合理,受力性能好,充分发挥了钢材的优势,所以被广泛地应用到钢结构以及钢–混凝土组合结构住宅、工业建筑与厂房当中 [1]。另外,其它常用的型钢有H型钢、冷弯薄壁型钢、压型钢板等钢材。

Figure 1. Schematic diagram of I-beam steel beam
图1. 工字形钢梁成品示意图
2. 有限元分析模型
2.1. 有限元建模设计
该构件模型为一根普通工字形简支钢梁 [2],两端支撑形式为铰接,跨度
,上翼缘承受2.5 × 105 N/m2的均布荷载,材料特性:弹性模量
,泊松比为
,屈服强度
N/m2。截面尺寸如图2所示。
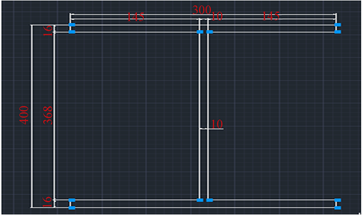
Figure 2. Schematic diagram of cross-section dimensions of I-shaped steel beams
图2. 工字形钢梁截面尺寸示意图
2.2. 有限元建模分析过程
计算模型采用实体单元进行建模,分析建完模型之后结果如图3所示,然后对该两端简支工字形钢梁上翼缘表面施加均布荷载,得到如图4所示的变形受力图 [2],由图4可知,对钢梁施加荷载,最大变形发生在简支钢梁跨中截面处,跨中处挠度、转角位移最大,这一结果也在图5所示的应力变形图云图模拟实验结果中得以验证,在图5中,红色部分所受弯曲应力比较大,应变变形也比较大,图6所示与未变形梁相比变形之后的梁发生了弯曲变形,这就要求钢梁自身的弯曲刚度要满足均布荷载作用下承载力的要求 [3]。对于两端简支的工字形钢梁来说在均布荷载作用下其跨中最大挠度可以参照下列公式计算。
对于均布荷载等截面简支梁:
对均布荷载变截面简支梁:
值一般取在1.05以内,刚度不够是可以调整工字形钢梁的截面尺寸,例如:可以增加截面的有效高度 [4]。

Figure 3. Finite element simulation undeformed graph
图3. 有限元模拟未变形图

Figure 4. Finite element simulation deformation map
图4. 有限元模拟变形图
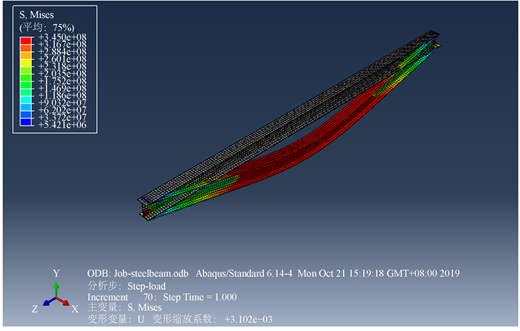
Figure 6. Unbalanced and deformed graphs comparing stress clouds
图6. 未变形图与变形图比较应力云图
通过图7与图8所示有限元模拟分析Mises应力云图相比较,发现对于两端铰接简支的普通工字形钢梁,在均布荷载作用下,其最不利位置在钢梁跨中处,在均布荷载作用下,钢梁跨中处出现最大弯矩,也就是会产生较大的挠曲变形,其变形变量、主变量、变形收缩系数达到最大 [4]。这就要求我们在实际施工和应用当中去考虑钢梁跨中受力弯曲变形比较大的问题,采取一定的措施减小钢梁跨中,在荷载作用下跨中最大弯矩值,防止钢梁的屈曲失稳(整体失稳和局部失稳现象) [4]。
整体失稳可参照如下公式:
其中钢梁的稳定系数
与轴对称截面形式有关,具体如下:

Figure 7. Stress cloud on undeformed graph
图7. 在未变形图上应力云图
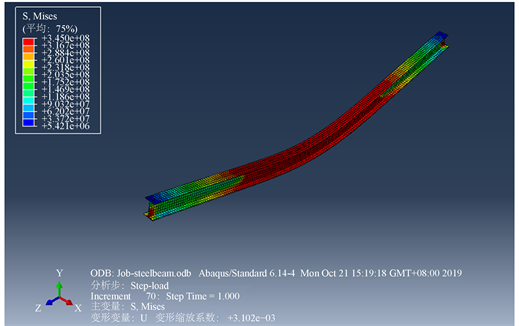
Figure 8. Drawing a stress cloud on a deformed graph
图8. 在变形图上绘制应力云图
单轴对称工字形截面简支梁:
纯弯曲的双轴对称工字形截面简支梁:
对于一般的受横向荷载或者不等端弯矩作用下的工字形截面钢梁(包括单轴与双轴对称工字形截面)应按下式计算整体稳定系数
:
对于均匀弯曲的受力钢梁构件,当
时,其整体稳定系数可按下式进行近似计算:
单轴对称时:
双轴对称时:
局部失稳可以分为钢梁翼缘的局部失稳和腹板的局部失稳,其中翼缘和腹板的局部失稳可以通过构造措施来实现,例如,翼缘可以控制翼缘的宽厚比来防止局部失稳,
;
同样腹板也可以按构造措施要求设置加劲肋来防止局部屈曲失稳,其具体计算公式不在一一列出 [5]。
2.3. 有限元建模结果分析
通过对有限元模拟模型进行可视化之后,所形成的应力云图,可以得到关于应力随时间变化的曲线,本次模拟所设时间长度为1,由图9所示可知在均布荷载作用下,在时间0.775 s之前钢梁应力随时间呈现线性增长,应力与时间呈现正比例线性关系,在时间达到0.775 s之后,应力达到峰值,达到峰值之后应力时间关系曲线进入水平段,应力不随时间的变化而继续增长,这就说明在这一时间段之内工字形钢梁,屈服强度达到极限屈服强度从而进入塑性阶段,应力不再变化 [6]。同样,由图10位移随时间变化曲线可知,钢梁结点处的变形位移在均布荷载作用下,在0.8 s之前没有明显变化,基本没有发生较为明显的变形,在0.8秒之后,随着加载时间的持续进行,发生了显著的位移变化,也就意味着,此时钢梁开始加快变形发展速度并且急剧增加,在经过一段时间的变形后,钢梁的变形达到极限状态,此时钢梁的变形将不再随着时间发生变化 [6] [7]。结点的位移时间变化关系曲线,大概可以分为这样三个阶段,第一阶段弹性阶段此时钢梁尚未进入屈服状态,位移增长速度缓慢;第二阶段,工字形钢梁部分进入塑性状态达到屈服强度,此时截面位移增长速度较快;第三阶段,整个工字形钢梁全面进入塑性状态,工字形钢梁截面位移快速增加 [7]。
由图11、图12所示,应力–应变随时间变化关系可知,钢梁在均布荷载作用下,在时间为0.775 s之前,在荷载作用下,应力随时间增长比较快,0.775 s之后应力基本达到最大值 [8],继续加载应力将会缓慢增长并逐渐趋于稳定,同样由图我们还可以得出,在0.8 s之后应变才逐渐增长扩展,在0.8 s之前钢
梁基本上不会产生应变,且由图12所示当应力增加到一定数值的时候,应变将不再发生变化,一般按照如下公式计算应力与应变的关系:
,此公式在弹性范围内使用 [8]。