杨氏模量测量误差研究及实验仪器的改进

Research on Young’s Modulus Measurement Error and Improvement of Experimental Instruments

摘要: 通过对金属丝杨氏模量测量原理和数据的误差分析，研究了影响实验误差的几个关键因素，提出了减小实验误差的设计方案。通过增加光杠杆数量扩大放大倍数；固定实验仪器之间的相对位置，减小测量的不稳定因素等方法改进实验装备。利用改进后的实验装置进行实验测量，可显著降低不确定度，提高了测量值的可信赖程度。

Abstract: Through the analysis of the principle and data error of the Young’s modulus of wire, several key factors affecting the experimental error are studied, and a design scheme to reduce the experi-mental error is proposed. The experimental equipment is improved by increasing the number of optical levers to enlarge the magnification; fixing the relative position between the experimental instruments and reducing the unstable factors of the measurement. The experimental measure-ment using the improved experimental device can significantly reduce the uncertainty and improve the reliability of the measured value.

1. 引言

杨氏模量是材料学中的一个重要的力学参数，表征了固体材料变形与应力之间的关系。金属丝杨氏模量的测量是大学物理实验中的一个典型的实验，使用了光杠杆放大法测量微小的形变量，实验装置包括读数显微镜、光杠杆、螺旋测微器等常用的测量工具，用逐差法处理标尺的读数，因此测量方法和工具都具有典型的代表性。然而，我们在实验过程中发现测量数据的误差较大和不确定范围较宽 [1] [2]。通过分析实验中误差的原因，设计了一种降低实验误差的新实验方案，并对设备进行了改进。

2. 实验原理

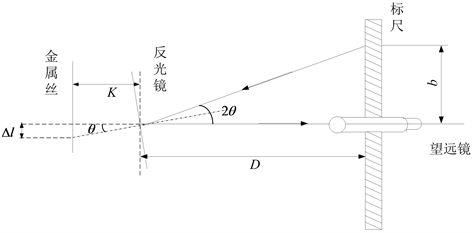
Figure 1. Experimental principle of Young’s modulus measurement

图1. 杨氏模量实验原理

在实验室施加的外力会使材料产生微小的变形，用常用的长度测量工具很难测量出来，但是过大的外力会使材料发生塑型形变，所以要通过放大法来测量。本实验通过光杠杆放大法将施加砝码产生的微小形变量进行了光学放大，通过公式计算出了杨氏弹性模量。实验原理如图1所示，光杠杆前足到金属丝的距离为 $K$。在砝码托盘上添加砝码，砝码的重力可看作外界对金属丝产生的一个外力 $F$，导致金属丝长度 $l$ 改变 $\Delta l$，金属丝带动光杠杆后足向下运动，光杠杆转动角度 $\theta$，当角度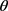很小时，可以有如下近似公式

$\theta \approx \tan \theta =\frac{\Delta l}{K}$ (1)

根据光的反射定律，入射角等于反射角，所以镜面转动角度 $\theta$ 时，光线经过反射后，反射光线转动 $2\theta$ 角度。用望远镜观察到标尺的刻度变化为 $b$，设标尺与光杠杆之间的距离 $D$，则

$\tan 2\theta \approx 2\theta =\frac{b}{D}$ (2)

公式(1)与(2)联立可得

$\Delta l=\frac{Kb}{2D}$ (3)

在金属丝的弹性范围内，根据胡克定律有

$Y=\frac{Fl}{S\Delta l}$ (4)

公式(4)表示杨氏模量 $Y$ 的测量公式，其中 $F$ 为砝码对金属丝产生的力， $\frac{F}{S}$ 称为应力， $S$ 为金属丝的横截面积。 $\frac{\Delta l}{l}$ 称为应变，代表金属丝的相对变化率，其数值与材料的性质有关。式中 $\frac{2D}{K}$ 叫做光杠杆的放大倍数，光杆杠的设计是巧妙的，它把不易测量的微小量放大成可以容易测量的量，但实验中仍有较多不确定因素，给实验的操作增加了难度，也使实验误差偏大。

3. 实验存在的误差分析

3.1. 仪器误差分析

实验要求望远镜轴线与光杠杆镜面法线重合，但实验时光杠杆与标尺分离，不易将其调整到同一条直线上。望远镜的观测视野较小，要快速的找到标尺刻度，对于初学者来说，掌握起来难度较大。而且，光杠杆与刻度尺之间的距离不易测量，实验结果的不确定性增加。实验过程中可能因不小心触碰实验仪器，使仪器发生位移，而导致光杠杆与标尺之间的距离改变，使实验的测量结果产生误差甚至错误 [3] [4] [5] [6]。

实验时，金属丝伸长 $\Delta l$，相应地光杠杆后足下降 $\Delta l$，因此光杠杆将绕其两前足的连线为轴转动，转动过程中，后足在水平方向上会发生移动，对金属丝产生一个横向的力，使金属丝偏离了竖直方向而增大了其与固定平台的摩擦，导致金属丝的受力大小不等于砝码的重力。实验时金属丝的受力情况与计算时假设的受力情况不同，会使计算结果产生较大的误差。

3.2. 实验操作的误差

金属丝在实验过程中会因拉伸而发生形变，随着金属丝的拉长，金属丝直径减少。若在实验开始时，托盘上没加砝码测量金属丝直径，金属丝没有完全拉直处于收缩状态，则测量得到的直径偏大。则会造成较大的误差。另外长时间将金属丝处于拉伸状态，金属丝会产生疲劳，添加砝码后读数的时间不同，测量的金属丝长度会有变化。在依次添加砝码和减少砝码时，测量的金属丝的长度会有很大的差别。

4. 设计方案

4.1. 实验装置的改进方案

针对标尺与光杠杆位置的不固定性，设计一个标有刻度的导轨，将光杠杆与标尺安装在导轨上，并可以自由滑动。这样可以方便调整光杠杆与标尺之间的距离，使光杠杆与标尺的位置固定，避免在测量过程中，操作人员因不小心触碰到实验仪器，而使标尺与光杠杆之间的距离发生改变，导致测量结果错误。为方便调节望远镜轴线与光杠杆镜面法线重合，改进了实验设备，添加了固定的导轨，将使实验操作难度下降，提高了实验效率。

将标尺换成精度更高的螺旋测微器，可显著提高测量精度 [7]。用激光发射器代替望远镜，调节激光发射器发射激光的方向，使光线经光杠杆平面镜反射到螺旋测微器上，读取螺旋测微器的刻度。这样观测到的数据，既方便又直观，降低了初学者实验操作的难度，使实验简便易操作。

针对金属丝偏离轴线，与固定平台产生摩擦的问题，改进方案的实验原理如图2所示。在金属丝两侧放置两个尺寸大小不一样的光杠杆，光杠杆1比光杠杆2的反射镜面大，两光杠杆在水平方向上对金属丝的力可以抵消，这样能使金属丝在竖直方向上保持不摆动，减少了其与固定平台的摩擦力，使金属丝在竖直方向上的受力近似等于砝码重力。实验时金属丝的受力情况与计算时的模拟受力情况更加接近，减少了计算时的误差。激光发射器发射的激光在反射镜组件上经三次反射，照射到标尺上，反射角度比入射角扩大了六倍。扩大了光杠杆的放大倍数，减小了标尺数据读取的实验误差。

平台上固定光杠杆前足的两个沟槽到金属丝的距离均为 $K^{\prime }$，其中在测量时，将光杠杆前足置于固定平台的沟槽内，将光杠杆后足放置在金属丝下端的夹块方柱体的平面上，并调节两后足长度相同。在砝码托盘上添加砝码，砝码的重力可看作外界对金属丝产生的一个外力 $F$，导致金属丝长度 $l$ 改变 $\Delta l$，金属丝带动光杠杆后足向下运动。当光杠杆转动角度 $\theta$ 足够小时，有：

Figure 2. Experimental schematic diagram of the improved device

图2. 改进后的装置原理图

$\theta \approx \tan \theta =\frac{\Delta l}{K}$ (5)

根据光的反射定律，入射角等于反射角，所以两镜面法线都转动 $\theta$ 角度，光线经过三次反射，最终的反射光线转动 $6\theta$ 角度。将螺旋测微器放置于原先的标尺位置，读出螺旋测微器的刻度为b。然后用米尺测量出标尺与到金属丝的距离 $D^{\prime }$，有图2得到：

$\tan 6\theta \approx 6\theta =\frac{b}{D^{\prime }}$ (6)

有公式(5)和(6)可得：

$\Delta l=\frac{K^{\prime }b}{12D^{\prime }}$ (7)

有式(7)可以看出光杠杆的放大倍数为 $\frac{12D^{\prime }}{K^{\prime }}$，因此光杠杆的放大倍数扩大六倍。

可以得到杨氏模量的计算公式

$Y=\frac{Fl}{S\Delta l}=\frac{12Fl{D}^{\prime }}{\pi d^2{K}^{\prime }b}$ (8)

其中， $d$ 为金属丝的直径， $D^{\prime }$ 为标出到金属丝的距离， $K^{\prime }$ 为反光镜1的镜面到金属丝的距离。

4.2. 实验操作方法的改进

为减小金属丝直径测量和加减砝码时平均值的测量误差。在测量金属丝的长度和直径时，要预加砝码，将金属丝拉直，以确保在金属丝上加相同的力时，金属丝的伸长量近似相等。测量金属丝直径时，在加不同砝码的情况下，对金属丝的不同位置多次测量，以防止因金属丝直径粗细不均或不直而使测量值与实际值之间有较大偏差 [8] [9] [10]。

4.3. 实验操作方法的改进

Table 1. Measurement data of wire diameter

表1. 金属丝直径的测量数据

金属丝直径的测量数据如表1所示，分别用改进前后的实验装置多次测量并计算金属丝的杨氏模量。比较改进前后测量的实验数据，分析此改进对计算结果的影响，并对是否需要进行这项改进做出判断，装置改进前后的数据如表2和表3所示。

Table 2. Measurement data of scale reading before device improvement

表2. 装置改进前的标尺读数测量数据

Table 3. Measurement data of scale reading after improvement of the device

表3. 装置改进后的标尺读数测量数据

测量数据的A类不确定度 [11] [12] [13] [14] [15] $u_A:u_A=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{\left(\Delta d_i-\overline{\Delta d}\right)}^2}}{n\left(n-1\right)}=\frac{\sigma }{\sqrt{n}}}$，根据实验仪器的精确度，得测量数据的B类不确定度 $u_B:u_B=\frac{{\Delta }_{仪}}{\sqrt{3}}$，其中 ${\Delta }_{仪}$ 为测量的仪器误差，计算不确定度： $u=\sqrt{u_{A+}^2{u}_B^2}$。通过计算得到实验改进前杨氏模量的不确定度 $u_{前}=1.28\times {10}^{11}\text{N}/{\text{m}}^2$，杨氏模量值 $Y=\left(1.75+1.28\right)\times {10}^{11}\text{N}/{\text{m}}^2$；实验改进后测量的不确定度 $u_{后}=0.26\times {10}^{11}\text{N}/{\text{m}}^2$，杨氏模量值 $Y=\left(1.77+0.26\right)\times {10}^{11}\text{N}/{\text{m}}^2$。已知待测的金属丝的杨氏模量理论值为 $1.80\text{N}/{\text{m}}^2$，根据计算数据分析可以看出，改进前后的实验装置所测量的数据有较大差异。通过对实验装置的改进，使实验数据更接近理论值，改进后实验装置测得的杨氏模量的不确定度量比改进前有明显的降低，实验测量的可靠性增强。

5. 结论

本文对用光杠杆测量金属丝杨氏模量实验的误差进行了讨论，并对实验仪器进行了改进研究，设计了导轨，使光杠杆可以方便移动，使用螺旋测微器代替了标尺，并增加了激光器，使光束经过光杠杆反射到螺旋测微器上。通过对金属丝杨氏模量测量原理和数据的误差分析，研究了影响实验误差的几个关键因素，提出了减小实验误差的设计方案。通过增加光杠杆数量扩大放大倍数；固定实验仪器之间的相对位置，减小测量的不稳定因素等方法改进实验装备。利用改进后的实验装置进行实验测量，可显著降低不确定度，提高了测量值的可信赖程度。