离心力对轴对称弯道河槽张力作用的研究

Study on the Effect of Centrifugal Force on River Channel Tension in Axisymmetric Bend

摘要: 采用镜像对称设置的匀速圆周运动系统，根据其向心力与离心力的作用与反作用力性质，在受约束离心力的作用下，全系统产生周期性运动，并应用于圆弧弯道水流离心力对河槽张力作用的计算。可用于圆弧弯道水流段水利工程的设计和防洪安全等领域。

Abstract: A uniform circular motion system model with symmetrical mirror image is adopted according to the action and reaction properties of centripetal force and centrifugal force. Under the action of constrained centrifugal force, the whole system generates reciprocating vibration. It is applied to the calculation of the effect of the centrifugal force on the tension of the river bed. It can be applied to the design of circular arc water conservancy projects and flood control safety.

1. 引言

尽管匀速圆周运动在确定轴上的投影是简谐振动，但未见像弹簧振子、单摆等其它简谐振动，对匀速圆周运动系统的功和能等问题作表述，究其原因是对匀速圆周运动物体系统的向心力与离心力是不是作用力与反作用力的关系问题。本文根据有关参考文献 [1] [2] [3] 和相关研究，明确了二者遵循牛顿第三定律。搞清楚这个问题，有益于全面掌握离心力的特点，正确指导相关问题的研究，进一步拓宽离心力作用的使用空间。

弯道河槽是水流经过的常见通道，流经弯道的水流，受河槽产生的沿弯道曲率半径法向(向心)力的作用，根据向心力与离心力的作用与反作用力(即符合牛顿第三定律)性质 [1] [2] [3]，弯道水流必然对该段河槽产生离心力的扩张作用，尤其是遇有水大流急的弯道急流情况，离心力扩张作用显著，产生的损毁作用增强。基于工程和防洪安全的实际需要，弯道水流段与直线水流段的水工程设计指标应相区分，相应调高弯道水流段水工程的设计标准，以抵抗水流离心力扩张作用的影响，确保水工程安全和功能的正常发挥。

2. 圆周运动物体系统的向心力与离心力是作用力与反作用力的依据

在质点仅受一物体的力的作用时向心力的反作用力就是离心力，两者大小相等、方向相反，但离心力却作用在给质点以向心力的物体上．换言之，向心力和离心力是作用和反作用，它们是作用在两个物体上的两个力。因此，它们不能平衡，不能抵销 [1] [2]。

向心力只产生于转动物体，不转动的物体没有向心力；向心力作用的效果是使本应作直线(沿切线方向)运动的物体，因受到垂直其运动方向指向圆心力的作用，才改作圆周运动的；转动物体对其实施向心力作用的物体施以向心力的反作用力——离心力的作用。向心力和离心力分别作用于两个物体，所在的同一直线不变，但随着转动物体位置的变动而改变，且符合牛顿第三定律 [3] [4] [5]。

3. 匀速圆周运动物体系统在受约束离心力作用下产生周期性运动

3.1. 构建物理实验模型

如图1，光滑平面，对称设置的两个质量均为m的球 $C_1,C_2$，二者做镜像的分别绕轴O、O’的匀速圆周运动，转动半径同为R，平板装置A全系统的质量为M (=km)。鉴于球 $C_1,C_2$ 采用镜像对称设置，为便于研究，分析以球 $C_1$ 为例(如图2) (球 $C_2$ 类同，讨论略。系统不计摩擦)。

Figure 1. Mirror symmetrical circular motion

图1. 镜像对称圆周运动

Figure 2. Centrifugal force analysis

图2. 离心力分析

图1中，两个镜像对称的作匀速圆周运动质点(球 $C_1,C_2$ )的向心力，在y轴方向上的合力为0，即系统向心力在y轴方向上的力受到约束，并始终处于平衡状态，只考虑二者向心力在x轴方向上的作用。

3.2. 匀速圆周运动系统离心力作用的解析

3.2.1. 匀速圆周运动系统离心力及在x轴方向上的冲量

如图2，圆周运动系统的向心力( $-{F^{\prime }}_R=-m\frac{v^2}{R}$ )与离心力( $F_R$ )遵循牛顿第三定律 [1] [2] [3]：

$F_R=-{F^{\prime }}_R,$

离心力在x轴上的分量：

$F_x=F_R\sin \varphi =-{F^{\prime }}_R\sin \varphi =-m\frac{v^2}{R}\sin \varphi$.

离心力在x轴上的分量的冲量：

根据动量和动量守恒定律，在任意时间段 $t_1\to t_2\left({\varphi }_1\to {\varphi }_2\right)$，以匀速v转动的 $C_1$ 向心力在x轴方向的分量所产生的冲量，其数值大小等于该向心力的反作用力——离心力在x轴方向的分量对平板A系统产生的冲量，( $C_1$ 在x轴方向的初速度 $v_{x_1}$，末速度 $v_{x_2}$ ；相对应平板A系统在x轴方向的初速度 $v_{1\left(M\right)}$，末速度 $v_{2\left(M\right)}$ )：

$\because v_x=v\cos \varphi$， $v_{x_1}=v\cos {\varphi }_1$， $v_{x_2}=v\cos {\varphi }_2$， $t=\frac{R\varphi }{v}$ ；

$\begin{array}{l}\therefore {\displaystyle {\int }_{t_1}^{t_2}{F}_x\text{d}t}={\bar{F}}_x\left(t_2-t_1\right)={\displaystyle {\int }_{t_1}^{t_2}\left(-m\frac{v^2}{R}\right)\sin \varphi \text{d}t}={\displaystyle {\int }_{{\varphi }_1}^{{\varphi }_2}\left(-m\frac{v^2}{R}\right)\sin \varphi \text{d}\left(\frac{R\varphi }{v}\right)}\\ =mv\cos {\varphi }_2-mv\cos {\varphi }_1=M{v}_{2\left(M\right)}-M{v}_{1(M)}\end{array}$

根据平均力算法：

${\bar{F}}_x=\frac{mv\cos {\varphi }_2-mv\cos {\varphi }_1}{t_2-t_1}$.

且 $v_{2\left(M\right)}=\frac{mv\cos {\varphi }_2-mv\cos {\varphi }_1+M{v}_{1\left(M\right)}}{M}$。

前半周(0→π)区间的冲量：

${\displaystyle {\int }_0^{\frac{T}{2}}{F}_x\text{d}t}={\bar{F}}_x\frac{T}{2}={\bar{F}}_x\frac{\pi R}{v}={mv\cos {\varphi }_2-mv\cos {\varphi }_1|}_0^{\pi }=-2mv$

${\bar{F}}_x=\frac{mv\cos {\varphi }_2-mv\cos {\varphi }_1}{t_2-t_1}=\frac{-2m{v}^2}{\pi R}$.

若 $v_{1\left(M\right)}=0$，且 $M=km$，

$v_{2\left(M\right)}=\frac{mv\cos {\varphi }_2-mv\cos {\varphi }_1}{km}=\frac{-2mv}{km}=-\frac{2}{k}v.$

设 $k=3$， $v_{2\left(M\right)}=-\frac{2}{3}v$ ； $k=2$， $v_{2\left(M\right)}=-v$。

后半周(π→2π)区间的冲量：

${\displaystyle {\int }_{\frac{T}{2}}^T{F}_x\text{d}t}={\bar{F}}_x\frac{T}{2}={\bar{F}}_x\frac{\pi R}{v}={mv\cos {\varphi }_2-mv\cos {\varphi }_1|}_{\pi }^{2\pi }=2mv$

${\bar{F}}_x=\frac{mv\cos {\varphi }_3-mv\cos {\varphi }_2}{t_3-t_2}=\frac{2m{v}^2}{\pi R}$.

3.2.2. 离心力在x轴上的分量所做的功

已知匀速圆周运动在x轴上的投影是简谐振动，根据有关文献 [1] [2] [3] [4] [5] 和研究，匀速圆周运动系统与弹簧振子、单摆等简谐振动一样，存在机械能守恒特征，即球 $C_1$ 向心力在x轴上的分量对其所做的功及所具有的能，完全转化为向心力的反作用力——离心力在x轴上的分量对系统A所做的功及所具有的能 [3] [4] [5] (假设机械能守恒)

$\begin{array}{c}{\displaystyle {\int }_{x_1}^{x_2}{F}_x\text{d}x}={\bar{F}}_x\left(x_2-x_1\right)={\displaystyle {\int }_{x_1}^{x_2}\left(-m\frac{v^2}{R}\right)\sin \varphi \text{d}x}\\ ={\displaystyle {\int }_{x_1}^{x_2}\left(-m\frac{v^2}{R}\right)}\sin \varphi \text{d}\left(R\sin \varphi \right)\\ =\frac{1}{2}m{v}^2{\cos }^2{\varphi }_2-\frac{1}{2}m{v}^2{\cos }^2{\varphi }_1\\ =\frac{1}{2}M{v}_{2\left(M\right)}^2-\frac{1}{2}M{v}_{1\left(M\right)}^2\end{array}$

由于被积函数在 $0\to \frac{\pi }{2}\to \pi$ ； $\pi \to \frac{3\pi }{2}\to 2\pi$ 两段的做功区间有正、负，根据力做功的方向，使用

$W={\displaystyle {\int }_a^b|f\left(x\right)\text{d}x|}=\pm {\displaystyle {\int }_a^{b}f\left(x\right)\text{d}x}$

前半周(0→π)区间做的功和振幅：

球 $C_1$ 在0→π区间的转动，相对应的系统A速度为 $v_{0\left(M\right)}\to v_M$。根据参考文献 [3] [4] [5] 和分析研究，离心力在前半周(0→π/2)、(π/2→π)做正功，假设系统机械能守恒：

$\begin{array}{c}{W|}_0^{\pi }={\displaystyle {\int }_0^{\frac{\pi }{2}}|{F^{\prime }}_x\text{d}x|}+{\displaystyle {\int }_{\frac{\pi }{2}}^{\pi }|{F^{\prime }}_x\text{d}x|}\\ =\frac{1}{2}m{v}^2+\frac{1}{2}m{v}^2=\frac{1}{2}M{v}_M^2-\frac{1}{2}M{v}_{0\left(M\right)}^2\end{array}$

在前半周(0→π)区间离心力对系统A作用的周期性运动存在，其振幅 $X_M$ ：

由 $M=km$，假设 $v_{0\left(M\right)}=0$，

$\begin{array}{c}{\displaystyle {\int }_{x_1}^{x_2}{F}_x\text{d}x}={\bar{F}}_x\left[x_{2\left(M\right)}-x_{1\left(M\right)}\right]={\bar{F}}_x{X}_M=m{v}^2\\ =\frac{1}{2}M{v}_{2\left(M\right)}^2=\frac{1}{2}km{\left(-\frac{2v}{k}\right)}^2=\frac{2}{k}m{v}^2，\end{array}$

由此可知，系统初始静止，只有当k = 2，能量守恒，周期性运动成立；对系统初速不为0，k ≠ 2的有关动力学问题在此不作论述。系统振幅：

$X_M=\frac{\frac{1}{2}M{v}_{2\left(M\right)}^2}{{\bar{F}}_x}=\frac{2}{k}m{v}^2\frac{\pi R}{2m{v}^2}=\frac{\pi R}{k}$，

当k = 2，即系统全质量是转动部分C₁质量2倍时，系统振幅：

$X_M=\frac{\pi R}{2}$.

3.2.3. 后半周(π→2π)区间离心力在x轴上的分量做的功和振幅

在后半周(π→2π)区间与前半周类同，离心力在后半周(π→3π/2)、(3π/2→2π)做负功(系统A在后半周区间速度为 $v_M\to v_{M_3}$ )：

$\begin{array}{c}{\left|W\right||}_{\pi }^{2\pi }={\displaystyle {\int }_{\pi }^{\frac{3\pi }{2}}|{F^{\prime }}_x\text{d}x|}+{\displaystyle {\int }_{\frac{3\pi }{2}}^{2\pi }|{F^{\prime }}_x\text{d}x|}\\ =\frac{1}{2}m{v}^2+\frac{1}{2}m{v}^2=-[\frac{1}{2}M{v}_{M_3}^2-\frac{1}{2}M{v}_M^2].\end{array}$

后半周(π→2π)区间离心力对系统A作用产生周期性运动的平均力和振幅 ${X^{\prime }}_M$ ：

${\bar{F}}_x=\frac{mv\cos {\varphi }_3-mv\cos {\varphi }_2}{t_3-t_2}=\frac{-2m{v}^2}{\pi R}$.

当k = 2时，系统后半周振幅：

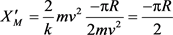。(同上半周)

3.2.4. 前后半周(0→2π)做功之和

$W={W|}_0^{\pi }-{\left|W\right||}_{\pi }^{2\pi }=0$.

前后半周离心力对系统A做功之和等于0，再次表明系统A做周期性运动的特征。

由于 $C_1,C_2$ 是镜像对称设置， $C_2$ 与 $C_1$ 类同， $C_2$ 讨论略。

结果：对质点球 $C_1,C_2$ 在前半周(0→π)区间的匀速转动，向心力的x轴方向分量为负方向，其反作用力——离心力的x轴方向分量为正方向，对系统作正功，使系统产生沿x轴正方向的运动；后半周(π→2π)区间的匀速转动，向心力的x轴方向分量为正方向，其反作用力——离心力的x轴方向分量为负方向，对系统作负功，使系统产生沿x轴负方向的运动，正负功数值相等，做功代数和为0，即系统沿x轴方向作周期性运动。且前后半周离心力沿x轴方向的分量的冲量值大小相等。

4. 轴对称 [6] 圆弧弯道水流离心力对河道张力作用的解析算法

自由状态镜像对称的匀速圆周运动系统，向心力与离心力符合作用与反作用性质，系统产生沿x轴方向宏观的周期性运动，由此可知弯道水流必然对河道产生法向张力的作用，尤其是水大流急的情况，对河槽产生的损毁作用强，有必要对此作研究。以轴对称圆弧弯道河槽为例，讨论水流离心力对河槽产生单向张力的算法。弯道水流是凹岸流速较大，凸岸流速较小，为突出效果和便与研究，轴对称弯道水流取平均流速v，以平均流量Q与水流断面面积S之比为参照依据 [7] [8] [9] [10]。

如图3，水流经过的圆弧弯道河槽示意图，有效半径R为圆心轴上O点至河槽水流质心点C(x,y,0)的距离，水流平均流速v，平均流量Q，如图4，水流断面高h，面积S， $C^{\prime }\left(x,y,z\right)$，讨论该段圆弧弯道水流沿x轴方向对河道的张力 $F_x$。

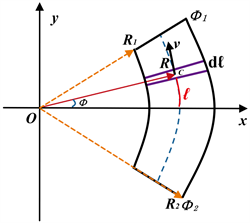
Figure 3. Schematic diagram of arc curve river channel

图3. 圆弧弯道河槽示意图

Figure 4. River cross section

图4. 河道横断面

采用微元法，在圆弧上的 $\mathcal{l}\left(=R\varphi \right)$ 段位置选取dℓ为水流元素的弧微分，水流元素质心 $C\left(R\cos \varphi ,R\sin \varphi ,0\right)$ 点的质量为m，根据匀速圆周流动水流的向心力与离心力遵循作用力与反作用力(即： $F_R=-{F^{\prime }}_R$ )的关系，先求出该水流元素离心力在x轴方向上的分量 $F_x\left(=-F_R\cos \varphi \right)$。

半径R的圆弧上，单位长度弧长上的水流元素个数为常量 $n\left(=\frac{N}{\mathcal{l}}\right)$，N为弧长ℓ上水流元素的总个

数，弧长ℓ的总水量为：

$M=Nm=n\mathcal{l}m$，

弧微分dℓ上水流元素的离心力在x轴方向上的分量 $F_{x}n\text{d}\mathcal{l}\left(=F_x\frac{N}{\mathcal{l}}\text{d}\mathcal{l}\right)$，在 $\left({\varphi }_1\to {\varphi }_2\right)$ 段上求积分得整

个弯道弧段水流在x轴方向上的张力：

$\begin{array}{c}{\displaystyle {\int }_{-\mathcal{l}}^{\mathcal{l}}{F}_x}n\text{d}\mathcal{l}=n{\displaystyle {\int }_{{\varphi }_1}^{{\varphi }_2}{F^{\prime }}_R\cos \varphi \text{d}\left(R\varphi \right)}=n{\displaystyle {\int }_{{\varphi }_1}^{{\varphi }_2}m\frac{v^2}{R}\cos \varphi \text{d}\left(R\varphi \right)}\\ =\frac{M}{\mathcal{l}}{v}^2\left(\sin {\varphi }_2-\sin {\varphi }_1\right)=2\frac{M}{\mathcal{l}}{v}^2\sin {\varphi }_2.\end{array}$

2012年7月24日长江三峡发生7万m³洪峰流量的罕见洪水，夹杂着泥沙直扑三峡大坝。如流经圆弧河槽段，平均河宽1000 m，平均河深5 m，圆弧河段有效长1000 m，有效半径5000 m， $\text{2}\varphi ={\text{17}}^{\circ }\text{27'}$，平均流速14 m/s，该段圆弧弯道水流沿x轴方向对河槽的张力：

${\displaystyle {\int }_{-\mathcal{l}}^{\mathcal{l}}{F}_x}n\text{d}\mathcal{l}=n{\displaystyle {\int }_{{\varphi }_1}^{{\varphi }_2}{F^{\prime }}_R}\cos \varphi \text{d}\left(R\varphi \right)=2\frac{M}{\mathcal{l}}{v}^2\sin {\varphi }_2=195673.5\text{N}=\text{19}\text{.57}\left(吨\right)$。

此虽为基础算法，对工程水力学的实际计算应用，基于弯道水流三维流的特点，以相同流速为前提，对弯道水流进行空间网格化编制，采用本文算法，对网格水流离心力沿x轴方向的分量对河槽的张力逐一计算并累加，即可求得弯道水流离心力对河槽的张力。有关实际算例此不做表述。

5. 结论

以匀速圆周运动在轴上的投影是简谐振动为基本，通过构造自由状态下镜像对称的圆周运动系统模型，确定圆周运动系统向心力与离心力遵循作用力与反作用力性质，对系统质量做优化设置和离心力方向做有效约束，整个系统在离心力作用下做周期性运动，使用此理论且用于弯道段河槽的沿平行于中心半径方向的张力计算。能够增强对圆周运动系统向心力与离心力的作用与反作用性质的认识，有益于拓展离心力应用研究的空间。