1. 引言
切换系统稳定性 [1] [2] 结果可以分为依赖切换序列的稳定性问题与切换序列不受限制的稳定性问题两类。脉冲的概念可以理解为在系统运行过程中一些变量在某一时刻瞬时的骤增或剧减。这种短暂的骤变会使系统运动状态产生很大变动,因此,这样的骤变不容忽视,将这类现象考虑到系统描述中就是常见的脉冲切换系统 [3] [4] [5]。正是由于这一系统更加准确地描述了物体的运动状态,并精确地描绘了物体的运动轨迹,才使得脉冲系统的应用愈加广泛。
时滞现象广泛的存在于系统控制、物理学、生态学等领域的研究中 [6]。正是由于其存在的普遍性才使得时滞现象成为人们在研究各种自然现象和社会科学时所不可忽视的因素。时滞的出现常常会破坏系统的稳定性,使系统产生变差,因此如何消除时滞对系统产生的不利影响就成了系统控制界研究的一个热门问题。
停留时间和平均停留时间这两个概念是Morse和Hespan ha提出的。在文献 [7] 中可以找到有关停留时间的详细介绍及一般理论,正如文中所给出的,停留时间就是指每个子系统被激活所需要的时间。在文 [8] 中,继停留时间的概念后又提出了平均停留时间的概念。“平均”二字体现在:在一个切换系统中,不要求每个子系统的激活时间都大于
,系统中也有可能出现激活时间小于
的情况,但综合所有子系统激活的平均时间大于
时,系统就会达到稳定。
本文研究了一类含时滞的脉冲切换系统稳定性问题,利用平均停留时间方法结合给定的几个引理研究了系统的指数稳定性和有限时间稳定性。本文所讨论的系统是在文 [9] 所给出的系统中引入时滞的结果。
2. 预备知识
在下文中,用符号“T”表示矩阵的转置,符号
代表n维欧氏空间,若向量
,则
;
R、
、
分别代表全体实数、正实数、负实数。
,
,
代表所有
实数矩阵,I为对应阶的单位矩阵。
考虑下列脉冲切换系统:
(1)
其中
代表系统状态,
表示初始状态,
表示时滞,
是定义在区间
的初始值函数。指示函数
表示子系统间的切换信号,
表示系统中所含子系统的个数,其中
是常数矩阵,
表示系统所含的非线性扰动,并且满足条件:
,
,
m是常数且
。
是常数矩阵,代表在切换时刻所产生的脉冲结果,且
,
表示切换信号
在区间
的切换次数,并且假设
。
定义1 [10] 指数稳定性的判据:如果系统(1)对于任意的切换信号
,在
时,存在正常数
和
,使得
,
则称系统(1)是全局指数稳定的。
定义2 [11] 平均停留时间定义:对于每个切换信号
,任意给定时间
,
定义为切换信号
在时间区间
上的切换次数。对于给定的
,
,定义
为切换信号的集合,满足:
其中
叫做平均停留时间,将
称为震颤界。
引理1 [12]
系统:
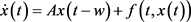 , (2)
, (2)
满足条件:A为n阶常数矩阵,w是实数,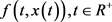 表示非线性函数。
表示非线性函数。
给定系统(2)的初始条件:
当 时
时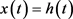 ;
;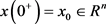 , (3)
, (3)
其中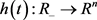 ,
,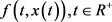 满足:
满足:
(i)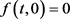 ;
;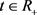 ;
;
(ii)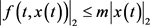 , m是常数。
, m是常数。
系统(2)在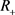 上存在解,表示为:
上存在解,表示为:
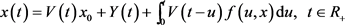 ,
,
其中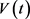 满足微分方程:
满足微分方程: ,
,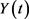 满足
满足
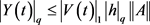
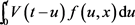 满足
满足
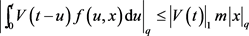 ,
,
给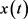 取范数得
取范数得
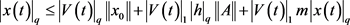
引理2 [13]
对于齐次方程:
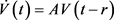 , (4)
, (4)
将方程(4)定义在区间 上,且初始条件
上,且初始条件 ,
,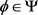 ,其中集合
,其中集合 表示所有定义在
表示所有定义在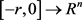 上的连续函数的全体。规定当
上的连续函数的全体。规定当 ,
,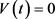 ,
,
齐次方程(4)的特征方程为:
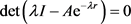 , (5)
, (5)
对任意的 ,
,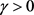 ,如果对于每一个矩阵A以及方程(5)的每一个特征根都满足
,如果对于每一个矩阵A以及方程(5)的每一个特征根都满足 ,则有常数
,则有常数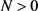 ,对于初始值为
,对于初始值为 ,
,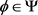 的方程(4)满足:
的方程(4)满足:
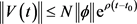 ,对于所有的
,对于所有的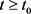 。
。
如果 ,则有
,则有
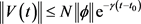 ,对于所有的
,对于所有的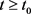 。
。
3. 主要结论
对于在时间区间 的任意切换信号
的任意切换信号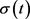 ,定义
,定义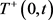 为特征根的实部
为特征根的实部 的所有子系统的总的活跃时间,
的所有子系统的总的活跃时间,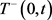 为所有特征根的实部
为所有特征根的实部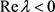 的子系统的总的活跃时间。
的子系统的总的活跃时间。 ,
,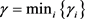 ,对任意给定的
,对任意给定的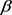 ,选择任意的常数
,选择任意的常数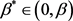 满足
满足
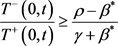 , (6)
, (6)
对于任意的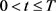 。
。
定理1对于给定的m和时间T,若切换信号满足条件(6),且存在正常数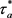 使得任意的平均停留时
使得任意的平均停留时
间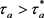 ,m满足
,m满足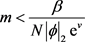 ,则系统(1)满足
,则系统(1)满足
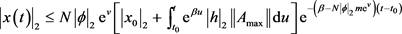 ,
,
即切换系统(1)是全局指数稳定的。这里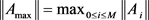 ,
,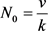 ,
, ,k和v满足
,k和v满足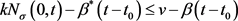 。
。
证明 定义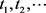 为切换发生的时间点,t满足
为切换发生的时间点,t满足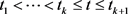 ,设
,设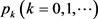 ,
,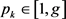 是切换信号
是切换信号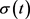 在
在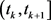 上的函数值。
上的函数值。
当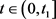 利用引理1可得
利用引理1可得
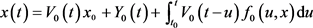 ,
,
以及
 .
.
基于脉冲结果在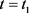 时的作用,有
时的作用,有
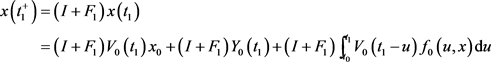 .
.
同样地,在时间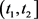 内可得
内可得
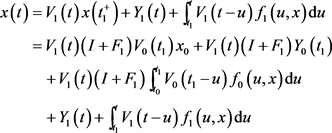 ,
,
及
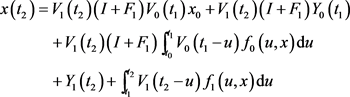
又
 .
.
通过归纳总结,可以推导出在时间区间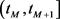 ,
,
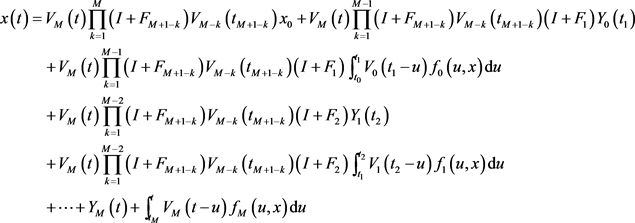 .
.
由于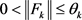 ,可以得到
,可以得到
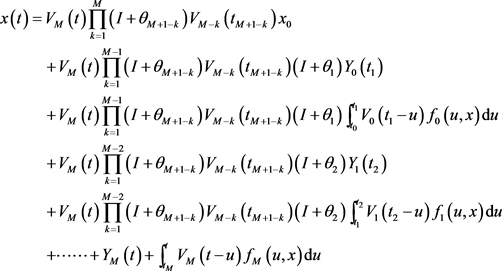 .
.
令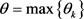 ,利用引理2,可以得到
,利用引理2,可以得到
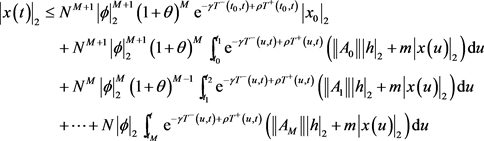 .
.
对于任意给定的 ,
,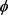 和N,可以找到常数k满足
和N,可以找到常数k满足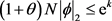 ;因此有,
;因此有,
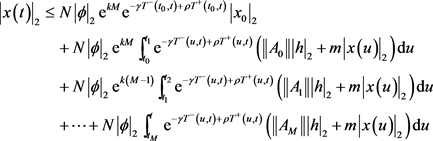
式(6)可以等价地写成
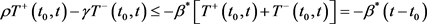 .
.
由上述不等式,可以得到:
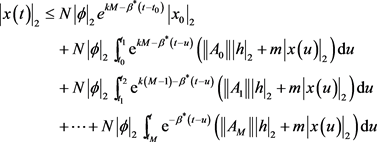 .
.
同时可以找到常数v满足:
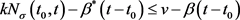 ,
,
其中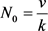 ,
,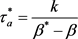 ,
,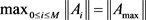 。因此有
。因此有
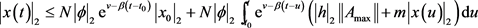 ,
,
将上式变形得
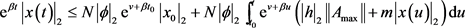 ,
,
上式也可改写为:

利用引理3,可以得到:
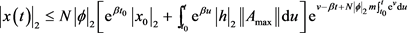
还可以写成
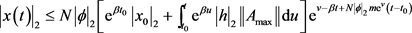
变形得:
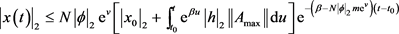
当m满足条件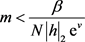 时,由此便可证得脉冲切换系统(3.1.1)满足定义2.3.1中所要求的条件,
时,由此便可证得脉冲切换系统(3.1.1)满足定义2.3.1中所要求的条件,
即对于满足定理条件的切换信号系统是指数稳定的。
4. 算例
考虑系统中所描述的参数:
 ,
, 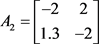 ,
,
显然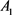 是不稳定的,
是不稳定的,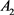 是Hurwitz 稳定的,由计算可得
是Hurwitz 稳定的,由计算可得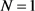 ,
,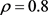 ,
,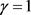 。
。
此外,脉冲矩阵:
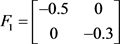 ,
, 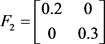 ,
,
其中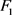 表示由子系统
表示由子系统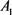 切换到子系统
切换到子系统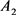 时所产生的脉冲矩阵,
时所产生的脉冲矩阵,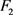 表示由子系统
表示由子系统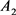 切换到子系统
切换到子系统 的脉冲矩阵,易得
的脉冲矩阵,易得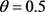 。
。
假设非线性扰动
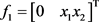 ,
,  ,
,
初始值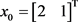 。
。
令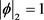 ,由不等式
,由不等式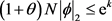 可以求得
可以求得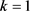 。
。
如果取 ,
, ,平均停留时间
,平均停留时间 ,
, ,
,
考虑系统总的作用时间为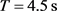 时的情况,图1所描述的是
时的情况,图1所描述的是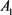 ,
,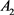 的激活时间分别是1 s和3.5 s时系统的运动轨迹,从图中可以清楚地看到系统(1)是指数稳定的。
的激活时间分别是1 s和3.5 s时系统的运动轨迹,从图中可以清楚地看到系统(1)是指数稳定的。

Figure 1. The state trajectory of the systems that the average dwell time 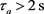
图1. 平均停留时间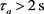 的系统运动轨迹
的系统运动轨迹
若切换系统的非线性扰动满足: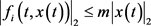 ,令
,令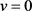 ,
,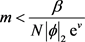 ,由计算可得
,由计算可得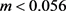 。
。
相应地,当非线性扰动:
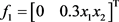 ,
, 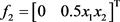 ,
,
可以得到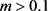 。图2是系统运动轨迹的模拟,这时系统已不满足指数稳定性。
。图2是系统运动轨迹的模拟,这时系统已不满足指数稳定性。
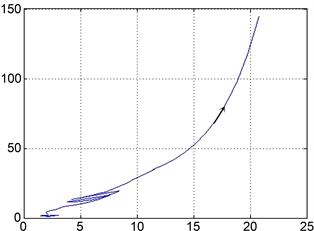
Figure 2. The state trajectory of the systems that the average dwell time 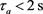
图2. 平均停留时间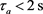 的系统运动轨迹
的系统运动轨迹
5. 结论
本文研究了一类脉冲切换系统的指数稳定性,系统中既含有Hurwitz稳定子系统又含不稳定系统,并将时滞与非线性扰动引入系统中,利用平均停留时间方法给出了使系统满足指数稳定性的充分条件。