热防护服的最优厚度设计

Optimal Thickness Design of Thermal Protective Clothing

摘要: 在高温环境下工作时，人们需要穿着专用服装以避免灼伤。专用服装通常由三层织物材料构成，记为I、II、III层，其中I层与外界环境接触，III层与皮肤之间还存在空隙，将此空隙记为IV层。确定高温作业下的人体皮肤温度以及热防护服最优厚度，有利于设计出更合理安全的热防护服。当人体处于高温环境中，穿着热防护服，分别讨论：1) 当环境温度为65℃、IV层的厚度为5.5 mm时，确定II层的最优厚度，确保工作60分钟时，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5分钟；2) 当环境温度为80℃时，确定II层和IV层的最优厚度，确保工作30分钟时，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5分钟。运用有限差分法、最小二乘法、双变量优化等方法分析数据，进而得到安全风险系数，以及确定热防护服各层材料的最优厚度。

Abstract: When working in a high temperature environment, people need to wear special clothing to avoid burns. The special clothing is usually composed of three layers of fabric materials, which are re-ferred to as layers I, II and III, wherein the layer I is in contact with the external environment, and there is a gap between the layer III and the skin, and the gap is recorded as an IV layer. Determin-ing the skin temperature of human body under high temperature operation and the optimal thickness of thermal protective clothing is conducive to designing more reasonable and safe thermal protective clothing. When the human body is in a high temperature environment, wearing thermal protective clothing, respectively, to discuss: 1) When the ambient temperature is 65˚C and the thickness of the IV layer is 5.5 mm, the optimal thickness of the II layer is determined to ensure that the skin of the dummy is 60 minutes after work. The outside temperature does not exceed 47˚C, and the time exceeding 44˚C does not exceed 5 minutes; 2) when the ambient temperature is 80˚C, the optimal thickness of layer II and IV is determined to ensure that the outside temperature of the dummy skin does not exceed 47˚C after working 30 minutes, and more than 44˚C for less than 5 minutes. The finite difference method, least squares method, and bivariate optimization method are used to analyze the data, and then the safety risk coefficient is obtained, and the optimal thickness of each layer of the thermal protective clothing is determined.

1. 引言

在高温环境下作业时，必须穿着高温作业专用服装以防人员被灼伤。专用服装一般由三层织物材料构成，记为I、II、III层。其中，Ⅰ层为最外层，直接与外界环境接触；Ⅲ层为最内层，与皮肤之间存在空隙，且将该空隙层记为IV层。高温作业服不仅要达到防止人员受到高温伤害的作用，同时还要尽可能降低服装的制作成本。

所给数据包括：1) 专用服装各种材料的参数值，包含该专用服装每层织物的密度、比热、热传导率、厚度等参数值；2) 假人穿着专用服装(II层厚度为6 mm、IV层厚度为5 mm)在75℃的高温环境中连续作业90分钟，得到假人皮肤外侧每秒温度的变化情况。

问题要求

根据以上题目背景及数据，建立数学模型讨论以下问题：

1) 根据专用服装材料的参数值，以及假人穿着专用服装(II层厚度为6 mm、IV层厚度为5 mm)在75℃的高温环境中连续作业90分钟，得到假人皮肤外侧每秒温度值，建立数学模型计算各时刻的温度分布。

2) 假人穿着专用服装(IV层的厚度为5.5 mm)在65℃的高温环境中连续作业60分钟，要求假人皮肤外侧温度最高极限为47℃，且超过44℃的时间低于5分钟。在满足以上要求的前提下，确定II层的最优厚度。

3) 假人穿着专用服装在80℃的高温环境中连续作业30分钟，要求假人皮肤外侧温度最高极限为47℃，且超过44℃的时间低于5分钟。在满足以上要求的前提下，确定II层和IV层的最优厚度。

2. 数据获取

为确定热防护服在高温下的温度分布情况属于稳态导热过程还是非稳态导热过程，根据附件所给数据，绘制每个时刻所测得的假人皮肤外侧温度变化图，如图1所示。

Figure 1. Temperature change diagram

图1. 温度变化图

稳态导热和非稳态导热做如下说明：

· 稳态导热：指物体各点温度不随时间变动的导热过程。

· 非稳态导热：指温度场随时间变化的导热过程。根据其特性可以分为两类非稳态导热：温度场随时间变化趋近于恒定值或温度场随时间变化作周期性变化。

由图1可知，假人皮肤外侧温度随时间增加不断升高，最后达到稳定状态，因此其温度分布规律属于典型的非周期性非稳态导热过程。

3. 模型建立

3.1. 热传递模型

图2表示了热防护服–空气层–皮肤系统 [1]，其中热防护服由三种织物材料构成，记为I、II、III层，织物层与皮肤间存在一定空隙，是空气层，记为IV层。

Figure 2. Thermal protective clothing-air layer-skin system

图2. 热防护服–空气层–皮肤系统

对于热防护服–空气层–皮肤系统的相关假设做如下说明：

· 热传递的方向垂直于皮肤，属于一维非稳态导热情况。

· 外界辐射进入第I层织物后被大量阻隔，因此忽略各织物层之间和空气层的热辐射。

· 空气层厚度值不超过6.4 mm，不考虑热对流的影响。

3.1.1. 传热微分方程的推导

热防护服的应用中，主要考虑热传导和热辐射两种热传递形式 [1]。其中热传导是由于温差而引起的能量转移，可由傅里叶定律 [2] 给出；热辐射包括吸收辐射和反射辐射，可由能量守恒定律 [2] 给出。

能量守恒定律

每一层织物的能量变化包括该层能量的吸收与反射，吸收率与反射率和为1，且内部无热源。令 $e\left(x,t\right)$ 为热能密度， $\varphi \left(x,t\right)$ 为热通量，由能量守恒可得

$\frac{\partial e}{\partial t}=-\frac{\partial \varphi }{\partial x}$。 (1)

令 $\rho \left(x\right)$ 为质量密度，单位质量的热能为 $c\left(x\right)T\left(x,t\right)$，则单位体积的热能可以表示为

$e\left(x,t\right)=\rho \left(x\right)c\left(x\right)T\left(x,t\right)$。 (2)

根据式(1)和式(2)消去热能密度 $\rho$ 后，得到能量守恒定律方程为

$\rho c\frac{\partial T}{\partial t}=\frac{\partial \varphi }{\partial x}$， (3)

其中 $\rho$ 为织物的密度，c为织物的比热，T为温度， $\varphi$ 为热辐射通量。

傅里叶定律

傅里叶定律表明在单位时间内的导热过程中，通过给定截面的导热量与该截面面积和截面法向上的温度变化成正比，其公式表示为

$\varphi =-k\frac{\partial T}{\partial x}$， (4)

其中，k为织物的热传导率，T为温度。

传热微分方程

由于热传递方向为垂直于皮肤方向，因此可将传热方向视为一维方向。将傅里叶定律(4)代入能量守恒定律方程(3)，得到一维方向的传热微分方程

$\rho c\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right)$。 (5)

3.1.2. 热防护服织物层中的热传递

由于只考虑一维的热传递，因此织物材料中的辐射能量在x点的热能一部分向左，一部分向右。令 $e_L$ 表示热能密度， ${\varphi }_L$ 表示在x点处向左辐射的总热辐射通量，由能量守恒定律可知

$\frac{\partial e_L}{\partial t}=-\frac{\partial {\varphi }_L}{\partial x}$。

若暂时不考虑向右辐射的热量，则x点处的净热能通量为 $\beta \left(\sigma T^4-{\varphi }_L\right)$，其中 $\beta$ 为一般材料单位面积的吸收能力， $\sigma$ 为斯蒂芬–波尔兹曼常数，其值等于 $5.67\times {10}^{-8}\text{W}/\left({\text{m}}^2\cdot {\text{K}}^4\right)$。因此 $\beta \left(\sigma T^4-{\varphi }_L\right)$ 是热能密度，则

$\beta \left(\sigma T^4-{\varphi }_L\right)=-\frac{\partial {\varphi }_L}{\partial x}$，

即

$\frac{\partial {\varphi }_L}{\partial x}=\beta {\varphi }_L-\beta \sigma T^4$。 (6)

同理，若暂时不考虑向左侧的热量，则x点处的净热能通量为 $\beta \left(\sigma T^4+{\varphi }_R\right)$，从而得到

$\beta \left(\sigma T^4+{\varphi }_R\right)=\frac{\partial {\varphi }_R}{\partial x}$，

即

$\frac{\partial {\varphi }_R}{\partial x}=\beta {\varphi }_R+\beta \sigma T^4$。 (7)

为更好地展示第I~IV层的热传递过程，用图3来表示。

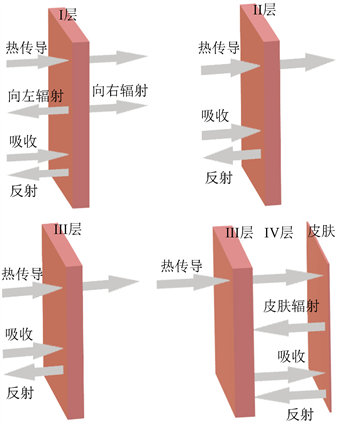
Figure 3. Schematic diagram of heat transfer from layer I to layer IV

图3. I层~IV层的热传递示意图

第I层织物的传热方程：

由于不考虑热对流的影响，因此第I层织物仅受环境的热传导和热辐射影响。令 $k_{\text{I}}$ 表示第I层织物的热传导率， $t_{\text{exp}}$ 表示高温作业的时间，则第I层织物的传热方程可表示为

${\rho }_{\text{I}}{c}_{\text{I}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k_{\text{I}}\frac{\partial T}{\partial x}\right)+\frac{\partial {\varphi }_L}{\partial x}-\frac{\partial {\varphi }_R}{\partial x}$， $\left(x,t\right)\in \left(0,L_{\text{I}}\right)\times \left(0,t_{\text{exp}}\right)$， (8)

其中， $L_{\text{I}}$ 为第I层织物的厚度， ${\rho }_{\text{I}}$ 为第I层织物的密度， $c_{\text{I}}$ 为第I层织物的比热， $k_{\text{I}}$ 表示第I层织物的热传导率， ${\varphi }_L$ 、 ${\varphi }_R$ 分别为向左和向右的辐射量，T为温度。

第II层织物的传热方程：

由于第I层织物阻挡掉了外界的大部分辐射，因此第II层织物主要受热传导影响，故第II层织物的传热方程表示为

${\rho }_{\text{II}}{c}_{\text{II}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k_{\text{II}}\frac{\partial T}{\partial x}\right)$， $\left(x,t\right)\in \left(L_{\text{I}},L_{\text{I}}+L_{\text{II}}\right)\times \left(0,t_{\text{exp}}\right)$， (9)

其中， $L_{\text{II}}$ 为第II层织物的厚度， ${\rho }_{\text{II}}$ 为第II层织物的密度， $c_{\text{II}}$ 为第II层织物的比热， $k_{\text{II}}$ 表示第II层织物的热传导率。

第III层织物的传热方程：

同理，第III层织物的传热方程表示为

${\rho }_{\text{III}}{c}_{\text{III}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k_{\text{III}}\frac{\partial T}{\partial x}\right)$， $\left(x,t\right)\in \left(L_{\text{I}}+L_{\text{II}},L_{\text{I}}+L_{\text{II}}+L_{\text{III}}\right)\times \left(0,t_{\text{exp}}\right)$， (10)

其中， $L_{\text{III}}$ 为第III层织物的厚度， ${\rho }_{\text{III}}$ 为第III层织物的密度， $c_{\text{III}}$ 为第III层织物的比热， $k_{\text{III}}$ 表示第III层织物的热传导率。

为表达方便，令 $L_2=L_{\text{I}}+L_{\text{II}}$， $L_3=L_{\text{I}}+L_{\text{II}}+L_{\text{III}}$， $L_4=L_{\text{I}}+L_{\text{II}}+L_{\text{III}}+L_{\text{IV}}$。

初始条件1：

将第I、II、III层看作一个整体织物层，则其初始条件为

$T\left(x,0\right)=T_1\left(x\right)$， $x\in \left(0,L_3\right)$。 (11)

边界条件1：

整个织物层的边界条件为

$-k_{\text{I}}{\frac{\partial T}{\partial x}|}_{x=L_3}={q_{\text{I}}|}_{x=0}$， (12)

$-k_{\text{III}}{\frac{\partial T}{\partial x}|}_{x=L_3}={\left(q_{\text{IV}}-k_{\text{IV}}\frac{\partial T}{\partial x}\right)|}_{x=L_3}$， (13)

$\left(1-{\xi }_1\right){\varphi }_L\left(0,t\right)+{\xi }_1\sigma t{T}^4\left(0,t\right)={\varphi }_R\left(0,t\right)$，

其中， $q_{\text{I}}$ 为第I层的热辐射热流密度， $q_{\text{IV}}$ 为第IV层空气的热辐射热流密度， $k_{\text{IV}}$ 为空气的热传导率， ${\xi }_1$ 为第I层左侧的辐射率。

边界条件2：

第I层与第II层之间的边界条件为

${T_{\text{I}}|}_{x=L_{\text{I}}}={T_{\text{II}}|}_{x=L_{\text{I}}}$，

$-k_{\text{I}}{\frac{\partial T}{\partial x}|}_{x=L_{\text{I}}}=-k_{\text{II}}{\frac{\partial T}{\partial x}|}_{x=L_{\text{I}}}$， (14)

$\left(1-{\xi }_2\right){\varphi }_L\left(L_{\text{I}},t\right)+{\xi }_2\sigma t{T}^4\left(L_{\text{I}},t\right)={\varphi }_R\left(L_{\text{I}},t\right)$，

其中， ${\xi }_2$ 为第I层右侧的辐射率。

边界条件3：

第II层与第III层之间的接触面应满足

${T_{\text{II}}|}_{x=L_2}={T_{\text{III}}|}_{x=L_2}$，

$-k_{\text{II}}{\frac{\partial T}{\partial x}|}_{x=L_2}=-k_{\text{III}}{\frac{\partial T}{\partial x}|}_{x=L_2}$。(15)

3.1.3. 热防护服空气层中的热传递

第IV层织物的传热方程：

第IV层为织物层与皮肤之间的空气层，考虑到假人皮肤对第IV层会进行热辐射，故将第IV层的热能加上皮肤对其辐射的热能，即为热传递总热能，由此得到热传递模型为

${\rho }_{\text{IV}}{c}_{\text{IV}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k_{\text{IV}}\frac{\partial T}{\partial x}\right)-\frac{\partial q_{\text{IV}}}{\partial x}$， $\left(x,t\right)\in \left(L_3,L_4\right)\times \left(0,t_{\text{exp}}\right)$， (16)

其中， ${\rho }_{\text{IV}}$ 为空气的密度， $c_{\text{IV}}$ 为空气的比热， $k_{\text{IV}}$ 为空气的热传导率， $q_{\text{IV}}$ 为空气的热辐射热流密度。

由于第IV层厚度狭小，可以假设其热传导是稳态的，因此可以将上述热传递模型解耦为

$k_{\text{IV}}{\frac{\partial T}{\partial x}|}_{x=L_3}=k_{\text{IV}}{\frac{\partial T}{\partial x}|}_{x=L_4}=h_{\text{IV}}\left({T|}_{x=L_3}-{T|}_{x=L_4}\right)$， (17)

${q_{\text{IV}}|}_{x=L_3}={q_{\text{IV}}|}_{x=L_4}=\frac{\sigma \left({T^4|}_{x=L_3}-{T^4|}_{x=L_4}\right)}{\frac{1}{{\epsilon }_{\text{III}}}+\frac{1}{{\epsilon }_{\text{IV}}}-1}$， (18)

其中， $h_{\text{IV}}$ 为外界环境到第I层的热对流系数， ${\epsilon }_{\text{III}}$ 、 ${\epsilon }_{\text{IV}}$ 分别为第III层和第IV层的反射率。

初始条件2：

空气层的初始条件为

$T\left(x,0\right)=T_1\left(x\right)$， $x\in \left(0,L_4\right)$。

3.2. 最优厚度模型

针对第II层织物材料的最优厚度问题，可以将其看作一个优化问题，采用线性规划的方法构建最优厚度模型。可以利用安全风险系数 [3] 来构建相关函数表达式，并根据最小二乘法 [4] 计算皮肤外侧温度在满足条件的情况下，尽可能在高温环境坚持更长时间的最优解，并得到第II层的最优厚度。

I. 决策变量

分析题意可知，皮肤外侧温度随第II层厚度和时间的变化而变化，因此引入决策变量为第II层织物材料的厚度，即 $L_{\text{II}}$。

II. 目标函数

查阅相关资料可知，人体烧伤程度分为一级烧伤、二级烧伤和三级烧伤 [5] 等，其中，当皮肤温度达到44℃时，造成一级烧伤，而一级烧伤仅在表皮层发生热损伤，因此在安全范围内；当皮肤温度达到47℃时，造成二级烧伤，二级及以上烧伤均超出安全范围。

令P为频数因子， $\Delta E$ 为皮肤的活化能，t表示到达44℃后的持续时间，则人体皮肤距离二级烧伤可用安全风险系数(惩罚函数) f表示为

$f\left(t\right)={\displaystyle {\int }_0^{t}P{\text{e}}^{-\frac{\Delta E}{RT\left(x,t\right)}}\text{d}t}$， (19)

其中，R为理想气体常数，T为皮肤处的温度。当 $f<0.53$ 时，人体皮肤未被烧伤；当 $0.53\le f<1$ 时，造成一级烧伤；当 $f\ge 1$ 时，造成二级烧伤。

由于只有一个决策变量 $L_{\text{II}}$，因此将 $f\left(t\right)$ 替换为 $f\left(L_{\text{II}},t\right)$，用 $f\left(L_{\text{II}},t\right)$ 作为安全风险系数的函数表达式。为使安全风险系数尽可能小，需要求 $f\left(L_{\text{II}},t\right)$ 的最小值。

由题意可知，皮肤温度不能超过47℃，即不造成二级烧伤，因此不考虑 $f>1$ 的情况，则f与 $f^{*}=1$ 围成的面积越大，安全风险系数越低，其中 $f^{*}$ 表示恰好造成二级烧伤。由此得到目标函数为

$J\left(L_{\text{II}}\right)={\displaystyle {\int }_0^t{\left|f\left(L_{\text{II}},t\right)-f^{*}\right|}^2\text{d}t}$

该反问题可转化为一个最小二乘问题，将安全风险系数和温度的组合离散为若干个点，即 $\left(T_i,f_j\right)$，其中， $i=1,2,\cdots ,n$， $j=1,2,\cdots ,m$。由此得到离散的目标函数为

$J\left(L_{\text{II}}^{*}\right)=\min J\left(L_{\text{II}}\right)={\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^m{\left(f_i^j-f^{*}\right)}^2}}$，

其中， $L_{\text{II}}^{*}$ 为最优厚度。

III. 约束条件

由于不考虑 $f>1$ 的情况，因此约束条件为

$f\left(L_{\text{II}},t\right)\le 1$。

而60分钟内，皮肤温度超过44℃的时间不能超过5分钟，故有

$t\le 5$。

由于第II层的厚度范围为0.6~25 mm，则

$0.6\le L_{\text{II}}\le 25$。

IV. 最终模型

根据上述目标函数、约束条件可得第II层织物材料的最优厚度模型为

$\begin{array}{l}\min J\left(L_{\text{II}}\right)={\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^m{\left(f_i^j-f^{*}\right)}^2}}\\ \text{s}.\text{t}.f\left(L_{\text{II}},t\right)\le 1\\ t\le 5\\ 0.6\le L_{\text{II}}\le 25\end{array}$。 (21)

3.3. 双变量优化模型

由于有第II层和第IV层的厚度这两个变量，因此可以看作一个双变量优化问题，运用线性规划的方法构建第II、第IV层的双变量优化模型。

可以利用设计反问题 [4] 的方法，用安全风险系数来表示皮肤温度，通过求解安全风险系数来计算满足条件的最优厚度。

I. 决策变量

分析题意可知，皮肤外侧温度受第II、第IV层织物材料厚度的影响，因此引入决策变量为第II、IV层织物材料的厚度，即 $L_{\text{II}}$ 、 $L_{\text{IV}}$。

II. 目标函数

已知安全风险系数f可表示为

$f\left(t\right)={\displaystyle {\int }_0^{t}P{\text{e}}^{-\frac{\Delta E}{RT\left(x,t\right)}}\text{d}t}$，

其中，P为频数因子， $\Delta E$ 为皮肤的活化能，t为到达44℃后的持续时间，R为理想气体常数，T为皮肤处的温度。当 $f<0.53$ 时，人体皮肤未被烧伤；当 $0.53\le f<1$ 时，造成一级烧伤；当 $f\ge 1$ 时，造成二级烧伤。

由于决策变量为 $L_{\text{II}}$ 和 $L_{\text{IV}}$，因此将 $f\left(t\right)$ 替换为 $f\left(L,t\right)$，其中 $L=\left(L_{\text{II}},L_{\text{IV}}\right)$，用 $f\left(L,t\right)$ 作为安全风险系数的函数表达式。为使烧伤的风险尽可能小，需要求 $f\left(L,t\right)$ 的最小值。

由题意可知，皮肤温度不能超过47℃，即不造成二级烧伤，因此不考虑 $f>1$ 的情况，则f与 $f=1$ 围成的面积越大，安全风险系数越低，由此得到目标函数为

$J\left(L\right)={\displaystyle {\int }_0^t{\left|f\left(L,t\right)-1\right|}^2\text{d}t}$，(22)

将式(21)积分形式转化为离散形式，得到离散的目标函数为

$J\left(L\right)=\frac{1}{N}{\displaystyle {\sum }_{j=1}^N{\left|f\left(L,t\right)-1\right|}^2}$

III. 约束条件

由于不考虑 $f>1$ 的情况，因此约束条件为

$f\left(L,t\right)\le 1$。

而80分钟内，皮肤温度超过44℃的时间不能超过5分钟，故有

$t\le 5$。

由于第II层的厚度范围为0.6~25 mm，第IV层的厚度范围为0.6~6.4 mm，则

$0.6\le L_{\text{II}}\le 25$，

$0.6\le L_{\text{IV}}\le 6.4$。

IV. 最终模型

根据上述目标函数、约束条件可得第II、IV层织物材料的双变量优化模型为

$\begin{array}{l}\min J\left(L\right)=\frac{1}{N}{\displaystyle {\sum }_{j=1}^N{\left|f\left(L,t\right)-f^{*}\right|}^2}\\ \text{s}.\text{t}.f\left(L,t\right)\le 1\\ t\le 5\\ 0.6\le L_{\text{II}}\le 25\\ 0.6\le L_{\text{IV}}\le 6.4\end{array}$。 (23)

4. 模型的求解

4.1. 问题一的求解

有限差分法是一种微分方法，广泛应用于偏微分方程的求解。以式(8)、(9)、(10)、(16)建立以下热传递模型

${\rho }_{\text{I}}{c}_{\text{I}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k_{\text{I}}\frac{\partial T}{\partial x}\right)+\frac{\partial {\varphi }_L}{\partial x}-\frac{\partial {\varphi }_R}{\partial x}$， $\left(x,t\right)\in \left(0,L_{\text{I}}\right)\times \left(0,t_{\text{exp}}\right)$，

${\rho }_{\text{II}}{c}_{\text{II}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k_{\text{II}}\frac{\partial T}{\partial x}\right)$， $\left(x,t\right)\in \left(L_{\text{I}},L_2\right)\times \left(0,t_{\text{exp}}\right)$，

${\rho }_{\text{III}}{c}_{\text{III}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k_{\text{III}}\frac{\partial T}{\partial x}\right)$， $\left(x,t\right)\in \left(L_2,L_3\right)\times \left(0,t_{\text{exp}}\right)$，

${\rho }_{\text{IV}}{c}_{\text{IV}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k_{\text{IV}}\frac{\partial T}{\partial x}\right)-\frac{\partial q_{\text{IV}}}{\partial x}$， $\left(x,t\right)\in \left(L_3,L_4\right)\times \left(0,t_{\text{exp}}\right)$。

对于各层材料的偏微分方程组，采用有限差分法来处理，将这四层材料离散为若干个点。令 $0=x_0<x_1<\cdots <x_{m_1}=L_{\text{I}}$， $L_{\text{I}}=x_{m_1}<x_{m_1+1}<\cdots <x_{m_1+m_2}=L_2$， $L_2=x_{m_1+m_2}<x_{m_1+m_2+1}<\cdots <x_{m_1+m_2+m_3}=L_3$， $L_{\text{I}}=x_{m_1}<x_{m_1+1}<\cdots <x_{m_1+m_2}=L_{\text{II}}$。同样的方法，将时间离散成 $N+1$ 个点，分别为 $0=t_0<t_1<\cdots <t_N=t_{\text{exp}}$，令 $t_j=j\tau$，其中 $j=0,\cdots ,N$， $\tau =t_{\text{exp}}/N$。

以第I层为例，求其离散格式 [6]。令 $x_i=i{h}_1$，其中 $i=0,\cdots ,m_1$， $h_1=L_{\text{I}}/m_1$，则第I层的离散格式为

${\rho }_{\text{I}}{c}_{\text{I},i}^{j+1}\frac{T_i^{j+1}-T_i^j}{\tau }=\frac{k_{\text{I},i+1}^{j+1}-k_{\text{I},i}^{j+1}}{h}\frac{T_{i+1}^{j+1}-T_i^{j+1}}{h}+k_{\text{I},i}^{j+1}\frac{T_{i-1}^{j+1}-2T_i^{j+1}+T_{i+1}^{j+1}}{h^2}+{\theta }_i^{j+1}$，

第I层与空气的接触面的离散格式为

$-k_{\text{I},0}^{j+1}\frac{T_1^{j+1}-T_0^{j+1}}{h}=h_1\left(T_g-T_0^{j+1}\right)$，

第I层与第II层的接触面的离散格式为

$-k_{\text{I},m_1}^{j+1}\frac{T_{m_1}^{j+1}-T_{m_1-1}^{j+1}}{h}=-k_{\text{II},m_1}^{j+1}\frac{T_{m_1+1}^{j+1}-T_{m_1}^{j+1}}{h}$。

同理可得第II、III、IV层以及其接触面的离散格式，利用Matlab软件计算得到每一时刻每一坐标点处的温度。

将算法用流程图进行展示，如图4所示。

Figure 4. Flow chart of the finite difference method

图4. 有限差分法的流程图

取时间间隔 $\Delta t=25\text{s}$，筛选得到216条关于某一固定时刻各坐标点处的温度，其中10条记录的数据如表1所示。

Table 1. Table of material temperature distribution of each layer at part time

表1. 部分时刻的各层材料温度分布表

根据有限差分法，使用Matlab计算得出，在材料的10.2 mm处温升最低。因外界的高温环境与人体皮肤均为热源，且外界温度大于人体温度，所以在材料靠近人体皮肤处的温升最低，符合实际情况，说明计算得出的数据具有一定的可靠性。

为更加直观地展示特定时刻( $t=25\text{s}$ 、 $t=300\text{s}$ 及 $t=600\text{s}$ )材料各厚度处的温度分布，绘制“厚度–温度”二维图，如图5所示。

Figure 5. Two-dimensional map of temperature distribution at t = 25 s, t = 300 s and t = 600 s

图5. t = 25 s、t = 300 s及t = 600 s时刻的温度分布二维图

由图5可知， $t=25\text{s}$ 、 $t=300\text{s}$ 及 $t=600\text{s}$ 时刻每层厚度的温度变化程度十分相近，所以各个时刻的温度分布情况均相似，说明该曲线拟合程度较好。

为展示90分钟内所有时刻各层材料的温度，绘制温度分布的三维图，如图6所示。

Figure 6. 3D map of the temperature distribution of each layer of material

图6. 各层材料的温度分布三维图

图中黄色表示温度较高区域，蓝色表示温度较低区域。

由图6可知，厚度与温度大致成反比，人穿着热防护服时，越接近皮肤温度越低，但由于人体存在热辐射，因此接近人体皮肤的第IV层温度略有升高；温度与时间的变化成正比，人待在高温环境的时间越久，温度会逐渐升高。

4.2. 问题二的求解

该问题属于单变量最优问题，利用最小二乘法对 $\left(L_{\text{II}},f\right)$ 的九组数据：(7.6,1.05)、(7.7,0.39)、(7.8,0.07)、(7.9,0)、(8.0,0.1)、(8.1,0.3)、(8.2,0.6)、(8.3,0.92)、(8.4,1.43)进行曲线拟合，得到 $f-L_{\text{II}}$ 的拟合函数为

$f=0.0069L^2-0.1102L+0.4377$.

根据 $f-L_{\text{II}}$ 的拟合函数，绘制符合条件 $0.6\le L_{\text{II}}\le 25$ 的曲线，见图7所示。

Figure 7. Curve fitting of $f-L_{\text{II}}$

图7. $f-L_{\text{II}}$ 的曲线拟合图

由图7可知，当 $L_{\text{II}}=7.92\text{mm}$，f取到最小值0.01。因此，第II层的最优厚度为7.92 mm。

第II层的厚度 $L_{\text{II}}$ 不宜过大，否则会导致散热困难； $L_{\text{II}}$ 也不宜过小，否则外界热量将快速进入，因此猜想 $L_{\text{II}}$ 的厚度应是0.6~25 mm中间区域的一个值。本问题求解得到的最优厚度为7.92 mm，符合该猜想。

4.3. 问题三的求解

已知第I层、第III层厚度分别为 $L_{\text{I}}=0.6\text{mm}$ 和 $L_{\text{III}}=3.6\text{mm}$。利用热传导模型的偏微分方程组，通过有限差分法计算出环境温度为80℃时每一时刻每一坐标点处的温度，且满足工作时间为30分钟。同时绘制温度分布三维图，见图8所示。

Figure 8. Temperature profile at an ambient temperature of 80˚C

图8. 环境温度为80℃时的温度分布图

要满足工作30分钟时，假人皮肤外侧温度在 $44˚\text{C}<T\le 47˚\text{C}$ 之间的时间不超过5分钟这一条件，对80℃下的数据集进行筛选，得到总厚度在16.9 mm时满足要求，且为最小厚度，其中第II层织物材料的厚度为7.53 mm，即 $L_{\text{II}}=7.53\text{mm}$。

因此第IV层空气层的厚度为

$L_{\text{IV}}=L_{总}-L_{\text{I}}-L_{\text{II}}-L_{\text{III}}=5.17\text{mm}$。

根据各材料的参数值可知，第IV层的厚度范围为0.6~6.4 mm，计算所得的IV层最优厚度 $L_{\text{IV}}=5.17\text{mm}$ 在该范围内，因此认为是合理的。

所以，得到当环境温度为80℃时，II层和IV层的最优厚度分别为7.53 mm和5.17 mm。

5. 误差分析

由问题二最优厚度模型计算可知，满足要求的第Ⅱ层织物材料的最优厚度为7.9 mm。该厚度的前提条件为确保作业人员的皮肤温度不超过47℃，即确保作业人员不被二级烧伤。

但若受到其他影响，导致织物材料的参数值发生改变，则该临界值可能无法满足所需要求，将会灼伤作业人员。因此，在此基础上进行误差分析，适当改变第Ⅱ层织物材料的最优厚度，保证作业人员的安全。

由于达到一级烧伤后，皮肤温度会迅速升高，因此以一级烧伤为临界值，即人体皮肤温度不超过44℃，因此安全风险系数f应小于0.53，于是将最优厚度模型的约束条件改为

$f\left(L_{\text{II}},t\right)<0.53$。

由此得到考虑误差的最优厚度模型为

$\begin{array}{l}\min J\left(L_{\text{II}}\right)={\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^m{\left(f_i^j\left(L_{\text{II}},t\right)-f^{*}\right)}^2}}\\ \text{s}.\text{t}.f\left(L_{\text{II}},t\right)<0.53\\ t\le 5\\ 0.6\le L_{\text{II}}\le 25\end{array}$。

运用最小二乘法对模型进行求解，计算得到当 $L_{\text{II}}=8.73\text{mm}$ 时，安全风险系数最小。由此可知，为确保高温作业人员的安全，建议将第II层织物厚度在7.92 mm的基础上延长0.81 mm，即最优厚度为8.73 mm。

6. 结论

对于问题一，本文从热传导和热辐射两方面考虑热能的传递，首先根据能量守恒定律得到热辐射的能量守恒方程，再根据傅里叶定律得到热传导的方程表达式，两者结合得到一维方向的传热微分方程。然后根据该微分方程分别推导得到了第I、II、III、IV层的传热微分方程、初始条件以及每个接触面的边界条件，从而建立了热传递模型。利用有限差分法对模型的偏微分方程组进行求解，将四层物质进行离散，计算得到了某一固定时刻各层材料的温度分布二维图和每一时刻每一坐标点处的温度分布三维图。当t = 300 s时，各边界厚度为0、0.6、6.6、10.2、15.2 mm时所对应的温度分别为73.22℃、64.51℃、47.56℃、37.04℃、37℃。

对于问题二，属于单变量优化问题，利用安全风险系数得出关于温度、时间、距离的函数表达式，即建立正问题，再求出其对应的反问题。将反问题转化为具有最小二乘解的优化问题，确立了以安全风险系数为目标函数，不造成二级烧伤危险为约束条件的最优厚度模型，并对安全风险系数进行离散。然后运用最小二乘法研究安全风险系数f与第II层织物厚度 $L_{\text{II}}$ 的关系，得到函数表达式 $f=0.0069L_{\text{II}}^2-0.1102L_{\text{II}}+0.4377$。求解得到第II层织物的最优厚度为7.92 mm，安全风险系数为0.01，在安全范围内。

对于问题三，属于双变量优化问题，建立了关于温度、时间、距离的安全风险系数的函数表达式。通过确定相应的安全风险系数目标函数和约束条件，将目标函数的积分形式转化为离散形式，建立了双变量优化模型。然后利用最小二乘法和有限差分法对模型进行求解，用最小二乘法计算得到了满足约束条件的区间，缩小求解范围，并结合有限差分法，计算得到各个厚度的温度分布图，比较发现第II层和第IV层的厚度分别为7.53 mm和5.17 mm时，安全风险系数最小，故第II层和第IV层的最优厚度分别为7.53 mm和5.17 mm。

7. 模型评价与推广

7.1. 模型的优点

1) 对三层织物材料进行了充分分析，建立热传递模型，能够比较准确地计算出任意时间任意坐标点处的温度，从而判断出身着高温作业专用服的工作人员可以在不同温度下安全工作的最大时间；

2) 主要考虑了热辐射和热传导两种热传递方式，比较全面准确地计算了热量的传导和辐射。同时，考虑了高温作业专用服与皮肤之间的空隙，使模型更贴合实际情况；

3) 模型考虑了一维情况的热传递，一定程度上简化了模型和计算，操作更加便捷清晰。

7.2. 模型的缺点

1) 简单地将假人当作圆柱进行建模，没有考虑人体的实际情况来构建仿真人体模型，同时，忽略了人体可以通过出汗等方式散热，可能会对皮肤温度的变化造成影响；

2) 只考虑了热传递，忽略了空气中可能存在水蒸汽，会对热传递产生影响，在实际应用中可能会导致误差。

7.3. 模型的推广

本文的热传递模型可以较准确地计算出高温作业专用服的耐热性，为测试人体在不同温度下安全作业的最大时间提供支持和借鉴意义。可以应用在消防、冶金等领域，为需要在高温环境工作的人员设计适合的高温作业专用服装。