1. 前言及基础不等式
在许多金融、医学、控制等实际问题中,随机微分方程有着广泛的应用 [1] [2] [3]。
本文给出
表示d-维欧氏空间的闭子集,
表示d-维欧氏空间的紧子集。Hausdorff距离定义如下:
其性质(见 [4] 引理1.1.11)
(1)
更多的记号详见 [4]。
关于集值Lebesgue积分的不等式(见 [5] 定理5),
(2)
令
,
是所有的从
到
的Hausdorff距离连续的集值映射的全体。集值泛函随机微分方程
其中,
是
-值随机过程,映射
是可测的集值随机过程,映射
是有界可料可测的随机过程,
是集值平方可积鞅(见 [6] )。
2. 初值问题
不同于一般的随机微分方程,它应该是包含
在
的所有信息,而不是只有
是已知的,因此假设:
是
可测的
-值的随机映射,且满足
。
3. 方程解的存在唯一性证明
在集值泛函随机积分方程中,第一部分积分
是集值随机Lebesgue积分;第二部分积分
是随机过程关于集值平方可积鞅的随机积分(见 [6] )。为简化,在本文中我们省去了集值随机Lebesgue积分前的“(L)”及关于集值平方可积鞅的随机积分前的“(M)”。
1) 线性增长条件:对
,
常数a,s.t.对
2) Lipschitz连续条件:对
,
常数
,s.t.对
3) 集值积分不等式:
对于任意满足条件且为紧集值的初值
(即
为
值映射),集值泛函微分方程存在唯一强解。
证明:
存在性
定义
,并且令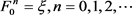 ,利用Picard迭代,对任意
,利用Picard迭代,对任意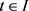 ,定义
,定义
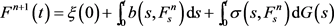

由(1)式,Hausdorff距离的性质,

由Cauchy-Schwarz不等式和集值积分不等式,
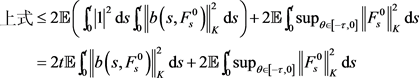
由线性增长条件,可知
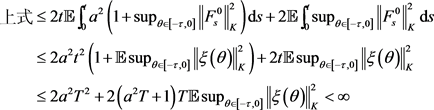
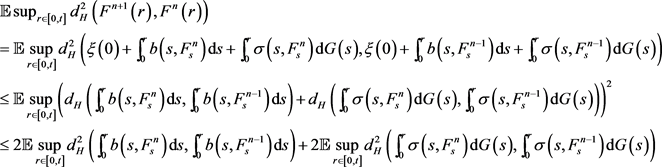
由(2)式,闭集值Lebesgue积分的不等式和集值积分不等式可得

由Lipschitz连续条件,可得
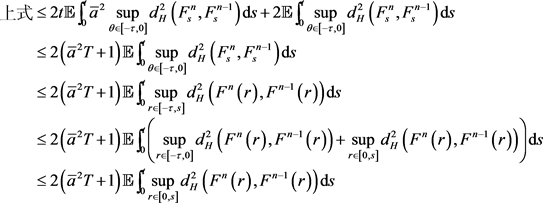
定义 ,因此有
,因此有
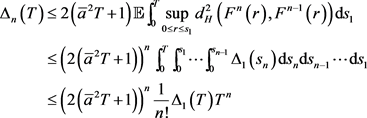
故有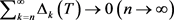 且
且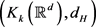 为完备距离空间,则存在
为完备距离空间,则存在 ,使得,
,使得,
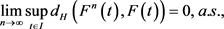
容易证明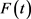 满足集值泛函随机微分方程且
满足集值泛函随机微分方程且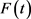 为连续适应的。
为连续适应的。
唯一性
采用反证法,假设存在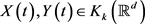 均为集值泛函随机微分方程的强解,
均为集值泛函随机微分方程的强解,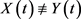 ,记
,记
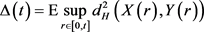
利用上面同样的方法,得
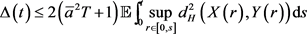
由Gronwall不等式,有 ,即唯一性成立。
,即唯一性成立。