基于SVM-KNN的股票价格预测

Stock Price Forecast Based on SVM-KNN

摘要: 本文利用支持向量机(Support Vector Machine, SVM)和K近邻(K-Nearest Neighbor, KNN)结合的算法研究股票价格的预测问题。选取反映股票变化的交易数据及其技术指标，包括成交量、收盘价、最高价、移动平均(MA)等，对上证综指进行涨跌趋势及收盘价格指数的预测。首先利用SVM对训练集进行预测，预测涨跌趋势，其次KNN对股票短期(1天)，中期(7天)和长期(30天)的价格进行预测，由此形成基于交易数据和技术指标的预测模型。最后得出此模型的综合平均相对误差(MAPE)和均方根误差(RMSE)。为了验证模型的有效性，根据模型预测结果构建新的投资策略，并利用真实数据进行投资，对大盘股指进行为期一个月的模拟投资。

Abstract: In this paper, the support vector machine (SVM) and K-nearest neighbor (KNN) algorithm were used to study the stock price forecasting problem, select the transaction data reflecting the stock changes and its technical indicators, including volume, closing price, highest price, moving average (MA), etc., forecasting the ups and downs and the closing price of the Shanghai Composite Index. Firstly, the SVM was used to predict the training set’s ups and downs. Then the training set used KNN to predict the short-term (1 day), medium-term (7 days) and long-term (30 days) prices of the stock, thus forming a forecast model based on transaction data and technical indicators. Finally, the MAPE and RMSE of this model were obtained. In order to verify the validity of the model, a new investment strategy was constructed based on the model prediction results, and the real data was used for investment, and the large-cap stock index was subjected to a one-month simulation investment.

1. 引言

在市场经济中，股票市场被认为是经济发展的晴雨表。并且，它对政治混乱、恐怖袭击和投资者心理等非经济因素最为敏感 [1]。股票市场的发展受到社会经济活动发展的影响，目前的研究主要基于复杂理论的发展。在大多数情况下，金融数据伴随着噪声、非线性和混沌的性质，使得数据在每个阶段会有不同的表现形式。因此，常用的统计方法中，例如移动平均、加权平均、卡尔曼滤波、指数平滑法、回归分析、自回归移动平均(ARMA)、集成移动平均(ARIMA)，就无法很好地对股票市场的指数进行预测。近来，与传统的统计方法相比，人工智能可以很好地解决股票市场所具有噪声、非线性和混沌的性质，因此本文尝试使用人工智能中的SVM和KNN方法对股票价格进行分类预测。

由于人们获取股票信息的渠道有限，常根据股票历史数据趋势结合技术指标进行涨跌预测，技术指标(移动平均MA、趋势指标MACD、指数移动平均EMA、动量MTM等)具有统计和经济上显著的样本预测能力。此外，技术指标和宏观经济变量在商业周期上提供了互补的信息；技术指标能更好地探测到商业周期峰值附近股票风险溢价的典型下降，而宏观经济变量更容易捕捉到周期低谷附近股票风险溢价的典型上升。随着机器学习、深度学习、数据挖掘领域的发展，越来越多的研究者利用股票市场的数据和机器学习的方法相结合进行预测 [2] [3] [4] [5]，从而更准确地把握股票涨跌趋势。研究表明这种方法具有较高的预测精度，并且通过多种技术指标对数据进行分析，具有良好的预测效果。

近年来，国内外许多学者利用机器学习、人工智能方法对股票市场进行了深入研究。神经网络 [6] [7] 、支持向量机 [8] 、遗传因子、粒子群优化等方法被用于股票价格预测 [9]。由于中国股票市场是一个新兴市场，有更大的不确定性。为了更准确地把握股票市场规律，已有学者应用了K-means [10] 、神经网络 [11] [12] 及其优化模式、深度学习 [13] 等方法研究股票深层规律，对股票价格趋势进行拟合，得到较好的效果。Dwiarso [14] 利用基于神经网络反向传播的梯度下降算法提高股票价格预测的准确性。Dai [15] 提出了将股票指数进行粒子模糊化从而利用SVM对之后的五个交易日的数据进行预测。因此，目前对于股票市场的研究是采用机器学习、深度学习等人工智能方法。由于股票市场的波动性较大，要实现较高的预测准确度有一定的难度，并且随着方法复杂程度的提高，容易出现过拟合的情况，且算法运行速度较慢，难以寻找较优的参数。

虽然研究者对股票市场规律进行了大量研究，但真正能够揭示股票市场深层次特征的、较准确预测股票价格的并不多。因此，为了克服以往研究的局限性，本文提出了一种新的SVM-KNN算法，利用SVM [16] 良好的分类效果来准确预测股票涨跌趋势，并利用KNN [17] 算法对股票涨幅进行预测，达到较好的预测股票价格趋势的目的。实验表明具有较准确的预测效果和预测精度。本文结构如下：第二部分对数据进行基本处理，第三部分对SVM和KNN算法的理论进行说明，第四部分为实证分析，第五部分进行模拟投资，第六部分为总结。

2. 数据与指标

2.1. 数据来源

本文选用的原始数据来自于锐思数据库，选择上证综指(上海证券综合指数简称“上证指数”或“上证综指”，其样本股是在上海证券交易所全部上市股票，包括A股和B股，反映了上海证券交易所上市股票价格的变动情况)从2008年1月2日到2014年12月31日的日交易数据，包括有：开盘价、最高价、最低价、收盘价、成交量。

2.2. 数据整理

本文用到的数据指标包括前一天收盘价、开盘价、最高价、最低价、收盘价、后一天收盘价、成交量。令 $U=\langle U_{prec},U_o,U_h,U_l,U_c,U_{nexc},U_{volume}\rangle$，其中 $U_p$ 代表前一天收盘价； $U_o$ 代表开盘价； $U_h$ 代表最高价； $U_l$ 代表最低价； $U_c$ 代表收盘价； $U_n$ 代表后一天收盘价； $U_v$ 代表成交量； $U_i$ 代表每一天的数据，如公式(1)所示：

$U=\left[\begin{array}{ccccccc}{u}_{1p}& u_{1o}& u_{1h}& u_{1l}& u_{1c}& u_{1n}& u_{1v}\\ u_{2p}& u_{2o}& u_{2h}& u_{2l}& u_{2c}& u_{2n}& u_{2v}\\ u_{3p}& u_{3o}& u_{3h}& u_{3l}& u_{3c}& u_{3n}& u_{3v}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ u_{np}& u_{no}& u_{nh}& u_{nl}& u_{nc}& u_{nn}& u_{nv}\end{array}\right]$ (1)

因为所得到的数据中不包括类标签，所以为了预测每一天的价格涨跌情况，本文引入了一个新的属性来识别类标签，即收盘价的变化 $y_i$，其中 $y_i$ 代表的是每一天股票 $u_i$ 的涨跌情况。计算公式如(2)所示：

$\Delta c^i=u_{i+m,c}-u_{i,c},\forall i=1,2,3,\cdots ,n-1$ (2)

每天的涨跌情况 $\Delta c^i$ 是以第i + m天和第i天的收盘价之差作为第i天的收益情况。如果 $\Delta c^i>0$ 则表示有盈利，反之，代表亏损。故 $\Delta c^i$ 代表了股票的走势方向，对盈利和亏损两种状况利用标签进行表示，如公式(3)所示

$y_i=\{\begin{array}{l}-1,\Delta c^i<0\\ 1,\Delta c^i\ge 0\end{array}$ (3)

收集到的所有的数据都要根据公式(4)进行归一化处理。

$u_{ij}=\frac{u_{ij}-u_{\min j}}{u_{\max j}-u_{\min j}}$ (4)

其中， $u_{ij}$ 代表第j天第i个指标的值， $u_{\max j}$ 和 $u_{\min j}$ 代表第j天所有指标的最大值和最小值。

2.3. 技术分析指标

HSU [18] 指出，在机器学习以前，金融经济学家一般更喜欢使用计量经济学，选择技术指标利用EMH模型来对股市进行分析。而技术指标依赖于过去的价格和成交量确定未来的价格趋势。现有的研究一般是基于多种技术指标构建交易策略提高盈利能力，包括过滤器规则 [19] 、移动平均线 [20] 、动量 [21] 和自动模式识别 [22]。因此，本文在收集到的原始数据的基础上加入一些重要的技术指标构成最终的特征向量。加入的技术指标如表一所示：

根据得到的技术指标，将已有的向量U进行扩充，最为最终的输入向量。

$U=\left[\begin{array}{ccccccccccccc}{u}_{1p}& u_{1o}& u_{1h}& u_{1l}& u_{1c}& u_{1n}& u_{1v}& T_{11}& T_{12}& T_{13}& T_{14}& T_{15}& c_1\\ u_{2p}& u_{2o}& u_{2h}& u_{2l}& u_{2c}& u_{2n}& u_{2v}& T_{21}& T_{22}& T_{23}& T_{24}& T_{25}& c_2\\ u_{3p}& u_{3o}& u_{3h}& u_{3l}& u_{3c}& u_{3n}& u_{3v}& T_{31}& T_{32}& T_{33}& T_{34}& T_{35}& c_3\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ u_{np}& u_{no}& u_{nh}& u_{nl}& u_{nc}& u_{nn}& u_{nv}& T_{n1}& T_{n2}& T_{n3}& T_{n4}& T_{n5}& c_n\end{array}\right]$ (5)

2.4. 误差分析

为了对模型的预测结果进行说明，本文选择用MAPE和RMSE来评价模型的预测能力。

$\text{MAPE}=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N\left|\frac{u_{i,\text{close}}-{\hat{u}}_{i,\text{close}}}{u_{i,\text{close}}}\right|\ast 100}$ (6)

$\text{RMSE}=\sqrt{\frac{1}{N}\underset{i=1}{\overset{N}{{\displaystyle \sum }}}{\left(u_{i,\text{close}}-{\hat{u}}_{i,\text{close}}\right)}^2}$ (7)

其中， $u_{i,\text{close}}$ 表示真实的收盘价， ${\hat{u}}_{i,\text{close}}$ 表示预测的收盘价，N代表测试数据的个数。

3. 基于SVM-KNN的预测模型

股票的涨跌和很多因素有关系，可以将其作为一种非线性、不确定的系统，本文利用从历史数据中获得信息，以此对股票涨跌趋势及价格进行预测。主要的思路：利用SVM对训练数据进行预测，并根据涨跌标签形成新的训练集，其次对测试数据利用SVM预测涨跌趋势，并对比标签一致的训练集，随后对每一个测试数据和其对应的训练集使用KNN对股票的价格进行预测，由此形成基于交易数据和技术指标的预测模型。

3.1. 支持向量机分类算法

支持向量机作为一种“监督性”的分类方法，是通过找到其超平面确定支持向量从而对数据进行分类。 [23] [24] 在线性可分的情况下，可以通过计算找到其最优超平面，如图1所示，其中圆形点和四边形点代表分类样本， $L_1$ 和 $L_2$ 代表最优超平面，二者之间的距离r称之为间隔(Margin)。

Figure 1. Linear plane separable hyperplane

图1. 线性可分情况的超平面

对于非线性的情况，要引入核函数，将输入的数据变换到高维空间中去，在新形成的空间中，计算其最优超平面，求得支持向量机。在本文中，将数据分为训练数据 和测试数据，对训练数据 $\left(u_i,y_i\right)$， $i=1,2,3,\cdots ,n-1$，利用支持向量机进行分类时，首先需要选择合适的核函数，其次利用SMO算法求得最优超平面和支持向量机，最后利用测试数据验证模型的准确度。

支持向量需要优化的问题目标的一般表达式如公式(7)所示：

$\min \Phi \left(x\right)=\frac{{\Vert w\Vert }^2}{2}+C{\displaystyle {\sum }_{i=1}^n{\xi }_i}$ (7)

s.t $\{\begin{array}{l}{y}_i\left(w^{\text{T}}{x}_i+b\right)\ge 1-{\xi }_i\\ {\xi }_i\ge 0,i=1,2,3,\cdots ,n\end{array}$

其中，C为惩罚参数， ${\xi }_i$ 为松弛变量。松弛变量说明了此分类器可以容忍分类错误的程度，当C越大时， ${\xi }_i$ 被压制，经验风险小，表示重视分类误差。

最终的对偶规划问题如公式(8)所示:

$\max Q\left(\alpha \right)={\displaystyle {\sum }_{i=1}^n{\alpha }_i}-\frac{1}{2}{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j\langle \varphi \left(x_i\right),\varphi \left(x_j\right)\rangle }}$ (8)

s.t $\{\begin{array}{l}{\displaystyle {\sum }_{i=1}^n{\alpha }_i{y}_i}=0\\ 0\le {\alpha }_i\le C,i=1,2,3,\cdots ,n\end{array}$

其中， $\langle \varphi \left(x_i\right),\varphi \left(x_j\right)\rangle$ 代表变换后的内积空间。分类超平面为：

$f\left(x\right)=\mathrm{sgn}\left\{\left(w^{\text{T}}\cdot \varphi \left(x\right)\right)\right\}+b=\mathrm{sgn}\left\{{\displaystyle {\sum }_{支持向量}{\alpha }_i^{*}{y}_i\langle \varphi \left(x_i\right),\varphi \left(x\right)\rangle }+b^{*}\right\}$ (9)

本文中，选择的核函数为径向基核函数(RBF)是：

$K\left(x_i,x_j\right)=\exp \left(-\gamma {\Vert x_i-x_j\Vert }^2\right),\gamma >0$ (10)

支持向量机的分类性能受核函数机及其参数、问题的复杂程度，及其分类面附近的噪音点的影响。

3.2. K近邻分类算法

KNN (K-Nearest-Neighbor)分类器是通过给定一个待识别的样本集，根据在训练集中寻找到最近的K个近邻，通过确定K的个数，从而将待识别样本进行归类。图2中给出的是在k = 5的条件下的分类状况。

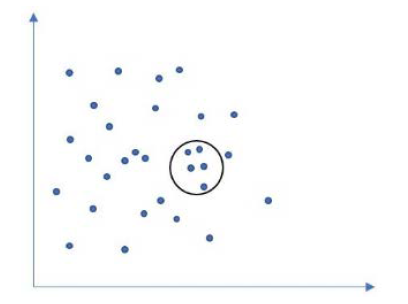
Figure 2. Classification when K = 5

图2. K = 5时的分类情况

3.3. SVM-KNN算法实现

本文所用算法的基本思路如图3所示，本算法共分为三个阶段。第一阶段，对收集到的数据进行预处理，依据表1加入技术指标，对数据进行描述，归一化处理后形成特征矩阵，并选择80%的数据作为训练数据，20%的数据作为测试数据；第二阶段，利用支持向量机对模型进行训练；第三阶段，对训练数据利用支持向量机得到分类指标，+1代表上涨，−1代表下跌，根据涨跌趋势，将训练数据集分为上涨集 $N_1$ 和下跌集 $N_2$，接着对每一个测试数据利用SVM得到分类指标P，并将分类指标P和新生成的上涨集 $N_1$ 和下跌集 $N_2$ 进行对比，选择指标一致的训练集 $N_i$ (i = 1, 2)，利用k近邻对 $N_i$ (i = 1, 2)中的 $\Delta c$ 计算。最终结果采用前一天收盘价加上预测的 $\Delta c$ 作为当天收盘价输出。

Figure 3. Algorithm flowchart

图3. 算法流程图

Table 1. Technical index calculation formula

表1. 技术指标计算公式

算法的运行流程如下：

4. 实例验证与结果分析

根据所选取的上证综指，利用模型预测提前1天、1周和1个月的收盘价变动。并且利用公式(4)进行归一化处理，处理后的数据如图4所示。按照所选取的从2008年10月31日到2014年12月31的数据，将其分为训练集以及测试集，该模型最终利用1200个数据进行训练，300个数据进行预测，所使用的技术指标如图4~7所示。模型的训练程度根据MAPE和RMSE进行评估。

Figure 4. Normalized closing price

图4. 归一化后的收盘价

Figure 5. MTM and MACD indicators

图5. MTM和MACD指标

Figure 6. MA and EMA indicators

图6. MA和EMA指标

Figure 7. RSI indicators

图7. RSI指标

图4为所选股票的收盘价趋势，图5~7为实验所选取的技术指标特征。MA的作用是消除股价随机波动的影响，寻找股价波动的平均趋势；EMA是指确定时间窗口下的平均值，数据点越近权重就越大，数据点越小权重越小；MACD是一种常见的技术分析工具，用于分析股票价格变化的强度、方向、能量以及趋势周期；RSI包括了交叉、数值、形态和背离等多方面的判断原则，RSI强弱指标的理论和实践极其适合于股票市场的短期投资；MTM又称动量指标，通过观察股价波动的速度来揭示股票价格反转的规律变化。通过这些技术指标特征，可以对股票价格规律进行更准确的刻画，便于SVM-KNN更准确地预测股票涨跌趋势。

对于SVM分类器，对参数C和γ进行优化，并选择最优参数如表2所示，其中C为SVM的松弛因子，C越小，模型的泛化能力就越强；γ为所选用径向基核函数的参数，γ值越小说明单个样本的影响力越大。对于KNN，根据文献阅读最终选择10作为K值。

Table 2. Parameter selection of SVM

表2. SVM的参数选取

表3说明了SVM对于短期、中期和长期的上证综指涨跌预测的情况。可以看出，SVM对于股票价格1天，7天，30天的涨跌预测准确率均在90%以上。

Table 3. SVM’s forecast of the ups and downs of the Shanghai Composite Index on different periods

表3. SVM对于不同周期上证综指的涨跌预测情况

图8~10所表示的为根据SVM-KNN对于1天、7天和30天的价格预测情况。可以看出，股票价格趋势拟合良好，所提算法能很好的预测股票价格趋势。表4是根据MAPE和RMSE计算的预测误差。

Table 4. MAPE and RMSE calculation errors

表4. MAPE和RMSE计算误差

表4是对模型进行评估，MAPE代表了平均绝对百分比误差，误差值越小，代表模型的拟合度越好，RMSE代表了均方根误差，是均方误差的算术平均值，评价数据变化的程度，RMSE的值越小，说明预测模型描述实验数据具有更好的精确度。

本文所提出的模型完全依赖于SVM的分类标签和KNN算法计算具有相似类别标签的K个邻域，将其均值与前一天的指数相加即可预测第二天的指数。该过程过滤了不需要参与预测的数据，从而降低了误差。

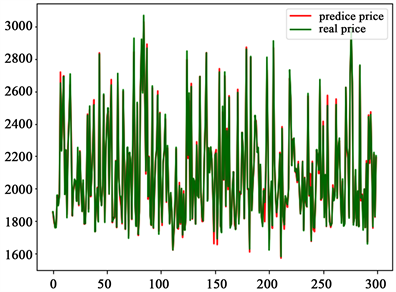
Figure 8. One-day ups and downs forecast

图8. 一天的涨跌预测情况

Figure 9. Seven-day ups and downs forecast

图9. 七天的涨跌预测情况

Figure 10. Thirty-day ups and downs forecast

图10. 三十天的涨跌预测情况

5. 模拟投资

为了更加充分的验证模型的有效性，本文利用对上证综指2014年11月19日到2014年12月31日的涨跌趋势进行预测，根据涨跌结果根据其收盘价进行模拟投资。

5.1. 构建投资策略

首先，根据SVM对上证综指2014年11月20日到2014年12月31日的涨跌趋势进行预测，再利用KNN输出30天的收盘价。接着，确定投资策略：规定在11月20日对上证综指以当日收盘价买入一股，随后观察涨跌趋势，在“当日上涨，明日下跌”的前一天卖出股票，并在“当日下跌，明日上涨”的前一天再次买入股票。如表5所示，买入的时间点应该为：11月20日、11月28日、12月20日和12月22日；卖出的时间点应该为：11月25日、12月19日、12月22日和12月23日。最后，根据中国股市的“T + 1交收”交易规则，本次买卖股票规定必须持有两天以上才可以卖出，因此，在模拟的30天内只进行两次交易。

Table 5. Thirty-day rise and fall

表5. 30天的涨跌情况

5.2. 计算收益

图11为预测30天的价格走势图。由图可知，30天内基本走势为上升，只有两次大规模的回落，为了保证盈利，可以在两次回落点前进行买卖。

t日实施投资并持有两天以上后将获得的股票当日收益率为：

$R_t=\frac{u_{t+n}-u_t}{u_t}$ (11)

其中， $u_{t+n}$ 为卖出时的收盘价， $u_t$ 为买入时的收盘价。

根据公式(11)，得到在两次交易中分别卖出股票后的当日收益率，根据公式(12)可以计算得出模拟投资期间的累计收益率。

$\text{CumR}=\underset{t=1}{\overset{n}{{\displaystyle \prod }}}\left(1+R_t\right)-1$ (12)

其中， $R_t$ 表示t日收益率，n表示做出投资操作的次数。

本文中，根据投资策略，30天内，第一次在11月19日买入股票，11月25日卖出股票，其收益率为0.053；第二次在11月28日买入股票，12月23日卖出股票，其收益率为0.15。因此，两次投资以后获得的累计收益率为0.21。

Figure 11. Thirty-day closing price

图11. 30天收盘价

5.3. 结果分析

夏普比率也称为夏普指数，是可以同时衡量收益和风险的综合指标，表示投资者每多承担一单位风险可获得的额外收益，计算公式如(13)所示：

$\text{Sharperatio}=\frac{E\left(R_p\right)-R_f}{{\sigma }_P}$ (13)

其中， $E\left(R_p\right)$ 表示投资组合的期望收益， $R_f$ 表示无风险利率， ${\sigma }_P$ 表示投资组合的标准差。如果夏普比率为正值，说明在衡量期内股票的平均净值增长率超过了无风险利率，在以同期银行存款利率作为无风险利率的情况下，说明投资股票比银行存款要好。夏普比率越大，说明股票的单位风险所获得的风险回报越高。夏普比率为负时，按大小排序没有意义。夏普比率是以资本市场线作为评价基准，对投资绩效做出评估。

本文根据公式(13)计算得出所构建的投资组合的夏普比率为1.618，由此说明该投资方案要好过银行存款，并且单位内获得正回报。

6. 总结

本文提出了基于SNM-KNN算法的股票价格预测方法，并结合相关技术指标于对上证综指短期、中期和长期的涨跌趋势进行预测。本算法首先通过技术指标对股票涨跌趋势进行初步刻画形成特征矩阵，然后利用SVM良好的分类能力预测股票涨跌趋势，同时结合KNN算法预测涨幅，实现准确预测股票价格的目的。最后，实验结果验证本文所提算法对股票市场指数具有较好的预测能力。