多因素驱动的配电变压器时变故障失效模型及应用

Time-Varying Failure Model of Multi-Factor Driven Distribution Transformer and Its Application

摘要: 现有配电系统可靠性评估大多基于设备长期历史数据的平均故障率，无法响应配电网运行状态以及运行环境的动态变化。文章综合考虑变压器因热老化、放电、受潮等因素引起的故障失效，建立环境温度与负荷特性相依的故障率模型和以“健康状态”为条件的故障率模型，进而获得多因素驱动的变压器短期可靠性模型。通过构建相关配电网的可靠性评估指标，基于变压器的短期可靠性模型，利用前推故障扩散法实现配电网的短期可靠性评估。最后通过算例验证了变压器短期可靠性模型的有效性，所得结果可实现配电网的故障预警，为配网的故障快速排除提供基础。

Abstract: Most of distribution system reliability evaluation is based on the average failure rate of the long-term historical data of the equipment, which cannot respond to the dynamic changes of the operation status and the operation environment. When synthetically considering the failure model of transformer caused by thermal aging, discharge, damp and other factors, the paper presents a failure model of environmental temperature and load characteristics, with the failure model based on health status. Therefore, we can gain the short-term reliability model of transformer driven by multi factors. With the reliability evaluation index constructed of distribution network, the short-term reliability evaluation of distribution network is realized by using the forward fault diffusion method based on the short-term reliability model of transformer. Finally, the validity of the short-term reliability model of the transformer is verified by a test system. The result can realize the fault early warning, and provide the basis for the rapid troubleshooting of the distribution network.

1. 引言

配电网承担着将电能从电源或输电网传输到不同电压等级用户的重要任务，直接与用户相连，对供电可靠性影响较大。据电力公司的统计，80%的用户非计划停电是由配电网故障引起的 [1]。配电网可靠性的准确快速评估是减少故障损失的基础，有着十分重要的意义。随着我国配电网的快速发展和社会用电需求的不断增加，对于配电网可靠性评估提出了更高的要求。

当前配电网可靠性评估的典型方法包括故障模式影响分析法、人工神经网络法，可靠性框图法、蒙特卡洛法和故障树分析法 [2] [3]。但目前应用于配电网可靠性评估的变压器故障率模型主要利用直观的数理统计模型确定 [4]，该类模型只是对变压器故障的一种简单模拟，忽略了变压器内部的复杂机理分析，无法反映变压器实时运行状态与运行环境对故障率的影响。针对这一问题，国内外学者针对变压器故障率模型进行了大量的研究，文献 [5] [6] 从设备寿命累积损耗的过程出发，采用描述老化过程的威布尔分布，建立了设备长期逐步失效的Arrhenius-Weibull模型。但是上述模型更侧重于变压器中长期老化的变化规律，无法反映短时超铭牌运行等短期因素对变压器时变风险的提高；同时上述模型在计算变压器热点温度时，忽略了绝缘油粘度的影响，存在一定的误差，影响了配电网可靠性评估的准确性。

单一特征量在变压器故障状态的表达上存在误差。因此文献 [7] 引入热动力学中焓的概念，根据标准生成焓对油中溶解气体进行加权，引入能量加权DGA概念，最后基于EWDGA和马尔科夫模型，提出了变压器潜伏性的故障率估计方法。张伯明等人同样考虑油气信息作为潜伏性故障发展情况的特征量，通过建立多状态马尔可夫过程模型对变压器的故障率进行了估计，并基于延迟半马尔可夫过程建立变压器时变停运模型 [6] [8]。但是该类模型仅仅是从变压器的角度出发建立了变压器的时变停运模型，没有从配电网可靠性评估的角度考虑变压器停运造成的影响。

综上所述，文章充分考虑绝缘油粘度的影响，准确计算变压器的热点温度。基于热点温度，结合变压器的寿命损耗，确定变压器的MTTF (平均无故障持续时间)，构建计及负荷特性以及环境温度影响的变压器实时故障率模型。针对上述故障率模型无法响应热老化以外的放电、受潮、冲击、形变等因素造成的故障，文中以“健康状态”为条件的故障率模型作为补充，建立变压器健康程度与故障率关联关系，提高变压器短期故障率模型的准确性。然后结合不同负荷需求，分析了变压器实时故障率的动态特性；针对配电网的风险评估，通过构建配电网的相关可靠性评估指标，基于元件优化编号，利用前推故障扩散法实现配电网短期可靠性评估，验证变压器故障率模型的可行性与准确性。

2. 多因素驱动的变压器故障率模型

2.1. 负荷特性与环境温度相依的老化失效模型

变压器的热点温度指的是电力变压器运行时绕组最热区域内达到的温度，是变压器绝缘失效的主要驱动因素。热电类比法将变压器的热传导过程简化为电路模型，可以直接反映变压器的物理过程，得到较为准确的特征温度 [9]。针对油浸式自冷的变压器，根据Susa D模型可知，其顶层油温为：

${\theta }_{\text{oil}}={\left(\frac{k^{2}R+1}{R+1}\right)}^{\frac{1}{1+n}}{\mu }_{\text{pu}}^{\frac{n}{n+1}}\Delta {\theta }_{\text{oil,R}}+{\theta }_{\text{a}}$ (1)

式中，k是负载系数，R是额定电流下负载损耗与空载损耗的比值， $\Delta {\theta }_{\text{oil,R}}$ 是额定负载下变压器顶层油相对环境温度的稳态温升，θ_oil、θ_a分别是顶层油温与环境温度，n是非线性指数，对于带负载的油浸式变压器，此处取0.25，μ_pu为任意温度下油粘度与额定油温下油粘度的比值，如下式所示：

${\mu }_{\text{pu}}=\frac{\mu }{{\mu }_{\text{R}}}=\exp \left(\frac{2797.3}{{\theta }_{\text{oil}}+273}-\frac{2797.3}{{\theta }_{\text{oil,R}}+273}\right)$ (2)

基于顶层油温，变压器的热点温度可由式(3)计算：

${\theta }_{\text{hst}}=k^{\frac{2m}{n+1}}{\mu }_{\text{pu}}^{\frac{n}{n\text{+1}}}\Delta {\theta }_{\text{hst,R}}\text{+}{\theta }_{\text{oil}}$ (3)

式中，m是非线性指数，此处取0.8， $\Delta {\theta }_{\text{hst,R}}$ 是额定负载下变压器绕组相对顶层油的稳态温升，θ_hst为绕组热点温度。

以绕组热点温度θ_hst为基准的相对老化率V在热点温度110℃的值为1 [10]，则其相对老化率为：

$V=\exp \left(\frac{B}{110+273}-\frac{B}{{\theta }_{\text{hst}}+273}\right)$ (4)

式中，B为经验常数。

由上式可知，在特定热点温度下变压器的期望寿命可由下式表示：

$T=N/V$ (5)

式中，N为变压器在基准热点温度110℃时的绝缘寿命，一般取180,000 h。

将式(4)代入式(5)可得：

$T=N\exp \left(\frac{15000}{{\theta }_{\text{hst}}+273}-\frac{15000}{110+273}\right)$ (6)

针对热老化引起的变压器绝缘失效问题，变压器的平均无故障持续工作时间(MTTF)与变压器的热点温度有关，因此计及环境温度与负荷大小的变压器故障率如下式所示：

$\lambda \left(k,{\theta }_{\text{a}}\right)=\frac{1}{T}N\exp \left(\frac{15000}{110+273}-\frac{15000}{{\theta }_{\text{hst}}+273}\right)$ (7)

2.2. 健康状态相依的潜伏性失效模型

单一特征量在设备故障状态上的表达可能存在偏差，随着近年来发现设备的健康状态对设备的故障率有直接的影响，国内外学者提出了以“健康状态”为条件的故障率模型，反映变压器的潜伏性失效模型。

健康指数(health index/indices, HI)是根据设备监测信息制定的反映设备健康状态的量化指标 [11] [12]。国外的学者对变压器的评分细则和权重计算进行过研究，从统计的角度建立了健康指数和设备故障率的关系。国内学者借鉴了国外健康指数的思路，也分别针对输电网和配电网设备制定了健康状态评分体系的企业标准。在此基础上，国家电网在2009年颁布的《输变电设备风险评估导则》用指数关系给出了健康指数HI和设备平均故障率λ的关系式：

$\lambda \left(\text{HI}\right)=k{\text{e}}^{-c\text{HI}}$ (8)

式中，k和c为采用统计数据拟合出的正常数，k为比例参数，c为曲率参数。

2.3. 健康状态相依的潜伏性失效模型

对于变压器而言，老化失效、隐性失效致停运模式等两类停运模式的机理是不同的，停运时间相互独立。从可靠性的角度看，两类种停运模式具有逻辑串联的关系，因此变压器的短期可靠性模型如下式计算：

${\lambda }_{\text{t}}=\lambda \left(\text{HI}\right)+\lambda \left(k,{\theta }_{\text{a}}\right)$ (9)

$t_{\text{t}}=\frac{\lambda \left(k,{\theta }_a\right)t_1+\lambda \left(\text{HI}\right)t_2+\lambda \left(k,{\theta }_a\right)t_1\lambda \left(\text{HI}\right)t_2}{{\lambda }_{\text{t}}}$ (10)

3. 输电线路安全裕度的表征配电网的短期风险评估

配电网主要基于用户数采用概率、频率和时间类指标来度量可靠性，重点表征用户的停电情况。文章采用的系统可靠性指标主要有以下三个：用户失负荷时间期望(LLTE)、用户失负荷概率期望(LLPE)、用户失负荷持续时间期望(LLDE)。

3.1. 用户失负荷时间期望(LLTE)

用户失负荷时间期望表示用户在单位时间内发生电力缺额的时间期望，可用用户停电时间和户数之比表示为：

$\text{LLTE}=\frac{{\displaystyle \underset{i\in \text{NS}}{\sum }\left(U_{\text{LP,}i}{N}_i\right)}}{{\displaystyle \underset{i\in \text{NS}}{\sum }{N}_i}}$ (11)

式中，U_LP,i表示负荷点i的平均失负荷时间；NS为系统所有负荷点集合；N_i为负荷点i的用户数。

3.2. 用户失负荷概率期望(LLPE)

失负荷概率期望表示系统用户在单位时间内失负荷的平均停电次数，可用用户停电总次数与用户数之比表示可表示为：

$\text{LLPE}=\frac{{\displaystyle \underset{i\in \text{NS}}{\sum }\left({\lambda }_{\text{LP,}i}{N}_i\right)}}{{\displaystyle \underset{i\in \text{NS}}{\sum }{N}_i}}$ (12)

3.3. 用户失负荷平均持续时间(LLDE)

用户失负荷平均持续时间表示系统中经受停电的用户在单位时间内单次停电的平均持续时间，可用用户停电时间总和与用户停电总次数之比表示：

$\text{LLDE}=\frac{{\displaystyle \underset{i\in \text{NS}}{\sum }\left(U_{\text{LP,}i}{N}_i\right)}}{{\displaystyle \underset{i\in \text{NS}}{\sum }\left({\lambda }_{\text{LP,}i}{N}_i\right)}}$ (13)

现有的网络连通性分析方法一般需对每个失效时间或每个负荷点进行一次网络拓扑搜索，计算量随网络规模的增大而急剧增大 [13] [14] [15]。文章参考文献 [16] [17]，基于元件优化编号，利用前推故障扩散法实现配电网短期可靠性评估。该方法仅需数次网络遍历便可确定所有元件停电的影响范围和隔离范围，枚举停电元件时无需再次遍历网络即可对节点进行分类并累加得到系统的可靠性指标，其可靠性评估流程如图1所示。

Figure 1. Reliability assessment algorithm flow

图1. 可靠性评估算法流程

4. 导线动态载流能力评估与运行温度预警

为验证计及负荷特性与环境温度的变压器故障率模型的有效性，文章通过计算IEEE标准定义的四种不同负载类型下变压器的故障率，分析变压器实时故障率的动态特性，为后续配电网的可靠性评估提供底层基础。算例采用的环境温度数据分别取自西南地区某地夏季和冬季某日24 h的温度数据，负载数据取自IEEE标准 [18]，分别如图2、图3所示。算例假设配电网采用的变压器为油浸式变压器，变压器短期可靠性模型的参数如表1所示 [19]。

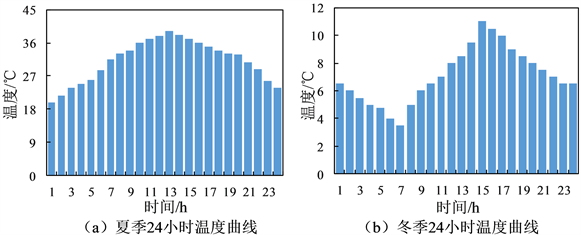
Figure 2. 24-hour ambient temperature curve

图2. 24小时环境温度曲线

Figure 3. Transformer load factor for four load types

图3. 四种负载类型的变压器负载系数

Table 1. Transformer short-term reliability model parameters

表1. 变压器短期可靠性模型参数

基于变压器的故障率模型，分别计算不同负载情况下24小时内变压器的实时故障率，如图4所示。

由图4可知，四种负载条件下，随着负载条件逐步增大，变压器的故障率随之增高。其中，短期急救负载与长期急救负载数据基本一致，只在12点时负载较长期急救负载高，因此在变压器在12时的故障率急剧提高；从夏、冬季比较来看，夏季环境温度高，在同一负载条件下，变压器夏季的故障率普遍高于冬季相应时刻。综上可知，变压器的故障率随着运行温度和负荷条件的变化呈正相关趋势，故文章提出的故障率模型可以有效地反映负荷特性和环境温度对变压器故障率的影响。

Figure 4. Transformer real-time failure rate curve

图4. 变压器实时故障率曲线

结合变压器健康状态相依的潜伏性失效模型，采用RBTS-BUS2系统对变压器的短期故障率模型进行验证，分析该模型的有效性与准确性。该系统有2个常开联络开关，58个节点，其中22个负荷点，图5中LP1~LP22表示负荷点 [20]。

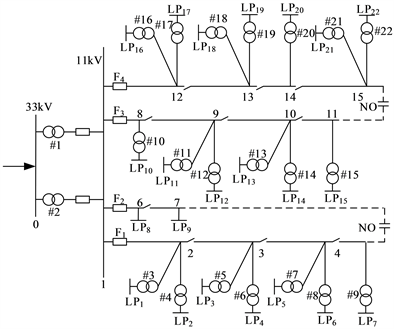
Figure 5. RBTS-BUS2 distribution network

图5. RBTS-BUS2配电网

通过在线监测、带电检测等手段获取变压器各部件的状态量，结合各部件的权重对变压器的扣分值进行综合计算变压器的健康指数，并根据式(8)计算变压器的实时故障率，结果见表2。

夏季的环境温度较高，变压器的故障率普遍高于冬季相应时刻，因此采用夏季的环境温度。为验证变压器短期故障率模型在配电网短期可靠性评估中的有效性，以RBTS-BUS2系统为研究对象，设置以下四种情形：

case1：假设RBTS-BUS2系统中的变压器承载正常周期性负载；

case2：假设RBTS-BUS2系统中#11变压器承载超铭牌过负荷运行，其余变压器承载正常周期性负载；

case3：假设RBTS-BUS2系统中的#11变压器承载长期急救负载运行，其余变压器承载正常周期性负载；

case4：RBTS-BUS2系统中#11变压器承载短期急救负载运行，其余变压器承载周期性负载。

针对以上四种情形，分别计算配电网的可靠性评估指标。具体如图6~8所示。

Table 2. Transformer short-term reliability model parameters

表2. 变压器短期可靠性模型参数

Figure 6. LPE in RBTS-BUS2 system

图6. RBTS-BUS2系统用户失负荷概率期望

Figure 7. LLTE in RBTS-BUS2 system

图7. RBTS-BUS2系统用户失负荷时间期望

Figure 8. LLDE in RBTS-BUS2 system

图8. RBTS-BUS2系统用户失负荷平均持续时间

仿真结果表明：1) 三个系统可靠性指标中，用户失负荷时间期望(LLTE)与用户失负荷平均持续时间(LLDE)对于配电网中元件运行状态改变的反应更为灵敏，可以有效地协助配电系统运行维护人员辨识配电网运行状态，为实现配电系统的故障预警提供基础。2) 当变压器承载周期性负载以及计划超铭牌运行时，变压器的故障率主要由健康状态相依的潜伏性失效模型决定，配电网的可靠性评估指标变化范围较小，配电系统运行维护人员需要加大对设备的日常维护和检修工作，改善设备的健康状态，降低配电网的时变运行风险。3) 当变压器承载长期急救性负载以及短期急救负载时，变压器的故障率主要由环境温度与负荷特性相依的实时故障率模型决定，配电网的可靠性评估指标变化范围较大，配电系统运行维护人员需要采取相关降风险措施，进行相应的负荷调整，确保变压器与配电网的安全可靠运行。4) 配电网的短期可靠性评估对于整个配电系统的运行状态感知较为准确，可以快速获取配电网运行风险较大的时间点，协助配网运行维护人员实现正确规划与紧急调度，具有实际价值。

5. 结论

文章综合考虑变压器因热老化、放电、受潮等因素造成的故障，建立多因素驱动的变压器短期可靠性模型。基于变压器的短期可靠性模型以及相关系统可靠性评估指标，利用前推故障扩散法实现配电网短期可靠性评估，最后利用RBTS-BUS2系统完成算例分析。经过算例分析，可获得以下结论：

1) 变压器运行状态的动态变化会影响变压器的实时故障率，进而影响配电系统的可靠性评估指标，利用构建的可靠性指标有效地协助配电系统运行维护人员辨识配电网运行状态，为实现配电系统的故障预警提供底层基础。

2) 当变压器承载周期性负载以及计划超铭牌运行时，变压器的故障率主要由健康状态相依的潜伏性失效模型决定，当变压器承载长期急救性负载以及短期急救负载时，变压器的故障率主要由环境温度与负荷特性相依的实时故障率模型决定。

3) 基于变压器的短时可靠性模型的配电网可靠性评估，可获取配电网运行风险较大的时间点，可协助运行人员进行相应的系统调整，为实现配电网的故障预警以及故障快速排除提供基础。