基于ARMA模型的二维码安全保险资金流控

Two-Dimensional Code Security Insurance Fund Flow Control Based on ARMA Model

摘要: 针对二维码盗取个人信息及诈骗的问题，构建一款二维码扫码保险的模型。本文引入纳斯达克综合指数(NASDAQ)，采用自回归移动平均(ARMA)模型对未来资金流动情况实施监测，对市场的现状进行分析及未来发展预测，其中资金流动及使用的策略是此服务能否顺利实行的关键。通过分析不稳定数据进行差分处理得到的自相关和偏自相关图和对平稳性的检验，设定模型形式和滞后阶数进行建模。通过残差检验，得到的残差图是随机正态分布的、不自相关的，可见残差是一段白噪声信号，其有用的信号已经都被提取到ARMA模型中。结果表明，使用ARMA模型能够很好地对未来资金流动情况进行预测。

Abstract: To solve the problem of two-dimensional code theft of personal information and fraud, a two-dimensional code scanning insurance model is constructed. In this paper, NASDAQ composite index is introduced, and the ARMA model is used to monitor the future capital flow, analyze the current situation of the market and predict the future development. Among them, the capital flow and the strategy of use are the key to the smooth implementation of this service. The autocorrela-tion and partial autocorrelation graphs obtained by differential processing of unstable data are analyzed and the stationary is tested. The model form and lag order are set for modeling. According to the residual test, the residual graph obtained is randomly normal distribution and non-autocorrelation, indicating that the residual is a segment of white noise signal, whose useful signals have been extracted into the ARMA model. The results show that the ARMA model can pre-dict the future capital flow well.

1. 引言

在科学技术高速发展的环境中，在大数据的影响下，人们的移动支付逐渐趋于大众化。从商业集团、房地产，到路边小吃摊，越来越多的人选择使用微信、支付宝、银联等扫码支付的方式。在生活中，二维码的主要用途可以概括成两方面：一是用于移动支付，二是进行产品的推广。二维码作为移动支付的方式已成为我们很多人的习惯，也是当今时代必不可少的支付手段。

二维码在为我们提供便利的同时，一些巨大的风险也随之而来。近年来，网络诈骗的方式不断更新升级，利用二维码的漏洞进行诈骗是一种更高级的电信诈骗方式 [1]。不法分子引诱用户扫码从而获取其个人信息、盗取银行账户，从而实施诈骗。因此，着手二维码保险的开发是顺应时代发展趋势，也是一个比较好的研究方向。

目前国内的学者针对保险资金的管理和运用提出相应对策，并对现阶段出现的问题进行分析。张杨 [2] 从保险资金投资收益率低，利差损较高，保险资金投资渠道狭窄的方面着手提出企业债，想到与银行合作开展贷款、金融租赁等业务的对策。郑颖 [3] 从信用、利率、流动性风险等方面考虑到保险资金的运用效率，形成了资产导向型与负债导向型两种资产负债管理。郑瑞娟 [4] 研究了保险公司资金管理的内部控制存在的问题：没有完善的绩效考核制度、管理监控力度不足、资金管理存在潜在风险等。而边江 [5] 针对如何优化保险公司对资金的管理也进行了分析。李振鹏 [6] 采用了分位数回归的方法，并应用他的var模型对于我国的保险资金筹集和运用的风险进行了实证测度。

本文主要是采用自回归移动平均(ARMA)模型对资金流动进行分析和监测，通过不稳定数据做差分处理得到自相关和偏自相关图，对差分后的时间序列进行平稳性的检验，再设定模型形式和滞后阶数进行建模。通过残差检验，得到的残差图是随机正态分布的、不自相关的，可见残差是一段白噪声信号，其有用的信号已经都被提取到ARMA模型中，由此得到的数学模型可对未来资金流动情况进行预测并得到很好的预测效果。

2. 保险投资市场分析

中国已成为最大的移动支付市场，据相关数据统计，在中国每三个手机用户就有两个在使用移动支付。2013年是中国移动支付行业的爆发元年，2013~2017年，第三方支付移动端交易规模由1.3万亿元增长至109.1万亿元，复合增长率高达235%，中国第三方支付移动支付2018年市场交易规模达190.5万亿元人民币 [7]，同比增速为58.4%。其中，支付宝以53.78%的市场份额排名第一，腾讯金融(含微信支付)以38.87%的份额排名第二，两者合计占据整个市场的92.65%。根据CNNIC公开数据显示 [8]，中国手机网民规模2017年继续增加，至7.52亿人次，同比增长8.25%。中国移动公布2018年11月份数据4G客户数净增413.2万户，累计达到7. 05亿户。消费的不断升级推动着第三方支付的快速发展。

支付领域APP活跃用户2017年呈现季节性波动，整体保持稳定，到四季度活跃用户超过5亿人次，环比增长达到3.89%。如图1，从2017年Q2到2018年Q2，互联网支付行业整体交易规模保持季度持续增长，共增加1.38万亿。

Figure 1. The size of China’s third-party payment market in 2017-2018

图1. 2017~2018中国第三方支付市场规模

3. 保险资金运用问题及策略

3.1. 建立ARMA (Auto-Regressive and Moving Average Model)时间序列预测模型

时间序列分析方法最初的自回归模型(AR)用于市场变化规律的预测，在此基础上数学家瓦格儿又提出了滑动平均模型(MA)和自回归移动平均模型（ARMA)，这3个模型奠定了时间序列分析理论的基础 [9]。自回归滑动平均时间序列预测模型是研究时间序列的重要方法之一。

ARMA模型属于时间序列分析中的一种，模型建立过程如图2所示。ARMA过程可能是AR与MA过程、几个AR过程、AR与ARMA过程的迭加，也可能是测度误差较大的AR过程。

公式定义： $y_t=\mu +{\displaystyle {\sum }_{i=1}^p{\gamma }_i{y}_{t-i}}+{ϵ}_t+{\displaystyle {\sum }_{i=1}^q{\theta }_i{ϵ}_{t-i}}$ (1)

式中， $y_t$ 是当前值， ${\gamma }_i$ 为自相关系数， $\mu$ 是常数项， ${\theta }_i$ 为滑动平均因子， ${ϵ}_t$ 为白噪声序列。

ARMA滞后算子(Lag operator)：

${ϵ}_t=\left(1-{\displaystyle {\sum }_{i=1}^p{\phi }_i{L}^i}\right)X_t=\phi \left(L\right)X_t$ (2)

其中 $\phi$ 表示多项式

$\phi \left(x\right)=1-{\displaystyle {\sum }_{i=1}^p{\phi }_i{x}^i}$ (3)

其自相关系数

$\rho \left(t,s\right)=\frac{COV\left(X_t,X_s\right)}{{\sigma }_t{\sigma }_s}$ (4)

最终可推出

$\left(1-{\displaystyle {\sum }_{i=1}^p{\phi }_i{L}^i}\right)X_t=\left(1+{\displaystyle {\sum }_{i=1}^q{\theta }_i{L}^i}\right){ϵ}_t$ (5)

Figure 2. Flow diagram of ARMA time series model

图2. ARMA时间序列模型流程框图

3.2. 保险资金流动可信性分析

对保险资金股市情况进行分析 [10]，本文引入纳斯达克综合指数(NASDAQ)作为参考指标(见图3)，进行市场现状分析及未来发展预测。通过对不稳定数据的差分处理消除不稳定因素，对处理后的数据进行平稳性检验，进而得到自相关和偏自相关图，再设定模型形式和滞后阶数进行建模计算。

ARMA模型要求时间序列必须是平稳的，对于平稳性的检验 [11]，本文采用ADF检验和KPSS检验，如图4所示。使用MATLAB进行运算，在直接运算的情况下没有通过检验，故需要取Y的对数做差分处理，消除指数增长趋势后再进行检验。此时依然没有通过检验，再次取对数。经过两次差分后得到的平稳性检验结果为dylog_h_adf = 1，dylog_h_kpss = 0，此时已得到平稳的时间序列。

接着确定模型阶数，可以通过自相关函数ACF和偏自相关函数PACF确定，如图5、图6所示。也可计算AIC，BIC等准则暴力选定阶数。首先用ACF和PACF估计模型阶数。

Figure 3. Import data

图3.导入数据

Figure 4. Stationarity test

图4. 平稳性检验

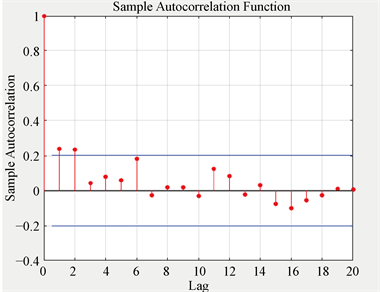
Figure 5. The autocorrelation function ACF

图5. 自相关函数ACF

Figure 6. Partial autocorrelation function PACF

图6. 偏自相关函数PACF

由自相关函数ACF和偏自相关函数PACF的图可看出本自相关和偏自相关因子很快落入随机区间，最后出现在阈值外的p = 2、q = 1。为了验证阶数选择的准确性，使用AIC、BIC准则验证模型阶数的选取是否正确。

从图7中可得p = 0、q = 2更加准确，即 $\text{ARMA}\left(p,q\right)=\text{ARMA}\left(0,\text{2}\right)$。

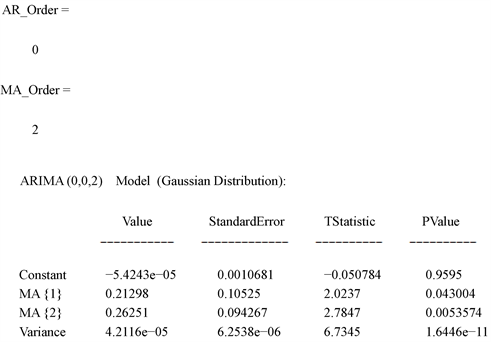
Figure 7. Correlation function graph after difference

图7. 差分后的相关函数图

为了确保确定的阶数合适，还需要进行残差检验。残差即原始信号减掉模型拟合出的信号后的残余信号。

从图8中可以看到，自相关函数ACF和偏自相关函数PACF没有超出阈值的点，且残差基本服从正态分布。通过Durbin-Watson对相关性进行检验，运算结果为2.0043，接近于2，说明残差不存在一阶相关性。上述检验说明ARMA模型符合要求。

预测结果及单步预测精度如图9所示。

Figure 8. Residual inspection results

图8. 残差检验结果

Figure 9. The fitted prediction

图9. 拟合预测情况

Table 1. Model order values and residual coefficients

表1. 模型阶数值及残差系数

由表1所求各值得出，ARMA (0, 2)模型具体的拟合结果可以写成

$X_t=-5.4243\times {10}^{-5}+{\epsilon }_t+0.21298{\epsilon }_{t-1}+0.26251{\epsilon }_{t-2}$ (6)

上述公式中的 ${\epsilon }_t$ 为残差序列。

若考虑到货币时间价值，n年后

$F=\left(X_t/F,i,n\right)={\displaystyle {\sum }_{n=0}^{n-1}{x}_t{\left(1+i\right)}^n}$ (7)

其中，i代表银行按揭利率。

3.3. 市场可控性分析

3.3.1. 互联网保险市场发展环境

在国民经济发展方面，总体情况来看我国的经济持续稳步发展,经济总量目前已超过10万亿美元，正逐渐发展成为中等居民收入的发达国家，人均收入已经超3000美元。在国内，消费对经济拉动作用凸显，人均保费日益增长，保险行业融资快速增长，互联网保险成为风口。

在科技和文化的发展方面，新四大科技发明中的三项——高铁、支付宝、共享单车都是涉及了二维码扫描信用卡和二维码的各个环节，移动二维码支付对于当代经济和社会的发展来说无疑是一种不可避免的发展趋势，在大家可以享受各种便利的同时也把威胁着人们的隐私和安全暴露在了大数据的背景下，因此二维码支付保险技术在国际上具有极大的重要性和发展应用空间。

3.3.2. 资金流通方向

主要通过网络进行数据处理，对二维码保险的项目的可行性进行跟踪。所有用数据汇总在资料库中，经过系统一系列的筛选、分析和计算，对资金流通方向进行系统分配，从而更好的把握资金的使用情况。

4. 结束语

本文使用ARMA时间序列模型对二维码扫描安全保险资金的股市未来发展趋势进行预测。此模型常被应用于数学和经济统计学，这种经济预测方法的优点是广泛地适用于很大一类实际经济问题，是目前国际上应用较为广泛的一种计量经济预测模型 [12]，在工业经济计量和建筑工程经济预测两个领域中都有着重要的作用，也是进行安全资金流控制的最好选择之一。

基金项目

沈阳航空航天大学2019大学生创新创业训练计划项目(201910143269)《二维码扫码安全保险》。