1. 引言
随着计算机技术,微处理器与电力电子技术的发展,逆变器控制系统也开始向数字化,智能化方向发展,并成为该领域的研究热点 [1]。SVPWM是近年发展的一种比较新颖的控制方法,是由三相功率逆变器的六个功率开关元件组成的特定开关模式产生的脉宽调制波,能够使输出电流波形尽可能接近于理想的正弦波形。空间电压矢量PWM与传统的正弦PWM不同,它是从三相输出电压的整体效果出发,着眼于如何使电机获得理想圆形磁链轨迹。SVPWM技术与SPWM相比较,绕组电流波形的谐波成分小,使得电机转矩脉动降低,旋转磁场更逼近圆形,而且使直流母线电压的利用率有了很大提高,且更易于实现数字化 [2]。
国内外学者对环流抑制提出了很多方法,硬件方面主要是从阻断环流通路考虑,如加入隔离变压器、增加硬件辅助电路等,但因提高了成本和并联系统的体积,已经鲜有人研究。软件方面,文献 [3] 提出了谐波消除PWM方法可以抑制零序环流的高频和低频分量,但会导致较高的开关损耗。文献 [4] 提出多载波PWM控制方案,通过废除零矢量的使用可以减小零序环流,但该方法对环流的抑制能力有限。文献 [5] 提出了非线性控制方法来抑制环流,但算法过于复杂,实际工程中应用困难。本文推导了T型三电平逆变器并联系统的平均模型,从零序环流的产生机理出发,对传统的SVPWM控制策略进行改进,设计出一种稳定的开环算法,并在SIMULINK中建立仿真模型验证了其可行性。
2. 逆变器并联系统数学模型
图1为两台T型三电平逆变器采用共直流母线和交流电网的结构并联组成的系统,选择直流负侧为参考点,则逆变器1的三相回路方程为(1),其中
是逆变器三相每个周期的平均电压;是电感电压;是电网中性点的电压。根据电感电压与电流的关系并考虑电感及线路内阻r,(1)可以改写为(2)
(1)
(2)
第x台逆变器的环流
为(3),假定逆变器三相的电感值是相等的,令(2)的三个回路相加,并将(3)代入得 (4)
(3)
(4)
则两台逆变器零序电压的差值为
(5)
如(5)所示,尽管零序环流的产生许多影响因素如硬件或者软件的不完美对称,并联逆变器的独立控制等,但最重要的还是并联逆变器的零序电压差异。由(5)可知零序环流的值与电网或者负载无关,主要取决于逆变器回路的零序阻抗,该阻抗为逆变器的电感内阻和线路内阻,因此非常小的零序电压差异将导致很大的环流。

Figure 1. Parallel T-type three-level inverter system
图1. 并联T型三电平逆变器系统
3. 基于SVPWM的逆变器并联模型分析
3.1. SVPWM算法原理
三电平的空间电压矢量分布图如图2(a)所示。分为六大扇区,每个大扇区又分为四个小扇区 [6]。根据空间电压矢量的幅度,可以将其分为表1中的四组。小矢量是多余的,成对小矢量产生相同的相电压。

Figure 2. (a) Basic space-vector diagram; (b) Zero sequence voltage represented by vector
图2. (a)基本矢量分布图;(b)矢量对应零序电压图
由于对称性,仅考虑扇区I就足够了,其他扇区都可以通过扇区I旋转一定角度得到。(6)所示的参考矢量Vref表示的交流侧电压可以在每个采样时刻由三个最近的矢量合成。
(6)
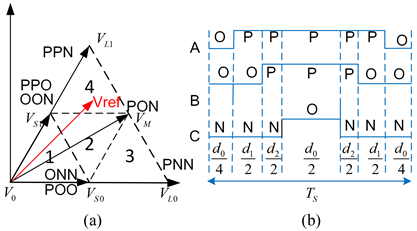
Figure 3. (a) Basic space-vector diagram; (b) Zero sequence voltage represented by vector
图3. (a) 参考矢量合成图;(b) 落入子扇区4的切换系列
当参考矢量落入I大扇区的4小区如图3(a)所示,根据SVPWM的矢量合成原则,参考矢量由距离最近的三个矢量合成,且由一个开关状态切换到另一个开关状态要求其开关管切换最少 [7]。则有(7)
(7)
其中
分别是空间矢量
的占空比,一个典型的开关矢量分配图如图3(b)所示,本文均采用N型小矢量为起始小矢量,采用P型小矢量会得到相同的结果。
3.2. 由SVPWM引起的环流
在实际应用中,由于硬件或软件的不对称性,每个转换器d轴和q轴的电流输出控制不能保持一致,导致每个转换器的参考矢量有幅值或相位的差异 [8]。如图4所示,由于参考矢量相位或幅值的差异,参考矢量将会以不同时间、不同位置从子扇区2跨越到子扇区4,由于当参考矢量在子扇区2和4内,逆变器的零序电压值不同,当两台逆变器跨越扇区的时间不同,则两逆变器零序电压不同,导致环流。
假定逆变器的直流电容环节是平衡的,则逆变器的零序电压可以通过式(8)求出:
(8)
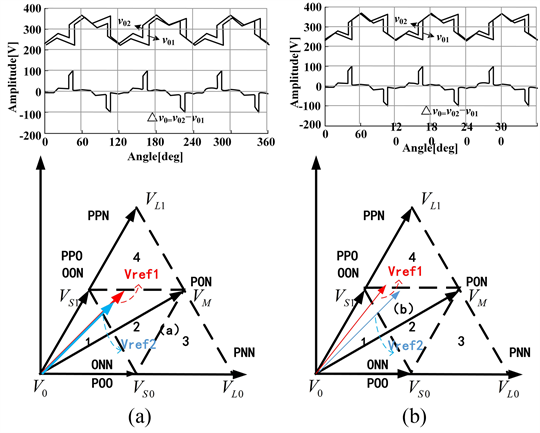
Figure 4. (a) Reference vector in phase with different amplitude; (b) Zero sequence voltage represented by vector
图4. (a) 参考矢量同相位不同幅值;(b) 参考矢量同幅值不同相位
根据图2(b)所示的不同开关状态对应的零序电压值可以计算出当参考矢量落入I大扇区的子扇区4时,零序电压值为(9)同理,当参考电压落入I扇区的子扇区2时,其零序电压为(10)
(9)
(10)
参考矢量在各个扇区的零序电压值在每个大扇区内子扇区1-3的零序电压一致,且它们的起始小矢量相同,而4的零序电压与其他三个扇区不同,起始小矢量也不同于其他三个扇区。起始小矢量决定了参考矢量的合成序列,相同的起始小矢量在一个周期内产生相同的零序电压,因此结合之前的分析,零序电压的跳变主要是起始小矢量的异步变化引起的。
3.3. NP电压偏差导致的环流
上述分析都是基于直流电容环节是平衡的,但实际中,即使是加入了中点平衡策略,中点电位也是处于波动状态。这也导致了并联运行的三电平逆变器中点电位电压由偏差,导致环流产生 [9]。控制中点平衡的策略有很多,本文采用的是加入调节因子y调节成对正、负小矢量的持续时间来实现。并引入新的变量e,e定义为
(11)
则I扇区的四个子扇区的值如12-15所示,其他扇区的表达式是对称的。
(12)
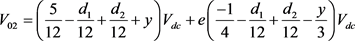 (13)
(13)
 (14)
(14)
 (15)
(15)
4. 改进后的空间矢量调制算法
4.1. 抑制环流的周期性跳变
如3.2节分析所述,零序环流的周期性跳变主要是并联三电平逆变器之间起始小矢量的异步变化,参考电压之间幅值和相位的差异将引起该问题。为了抑制幅值差异导致的零序电压差异,可以通过将每个大扇区的子扇区1和2进一步分为两个区域:1a、1b和2a、2b,如图5(a)所示,当Vref从a区域移动到b区域时,起始小矢量发生改变,即零序电压发生变化,越过后则不再改变,这样可以抑制幅值差异引起的环流。为了消除相位差引起的环流,可以重新分配矢量图的扇区号,如图5(b)所示,I扇区变为[−30˚, 30˚]。改进后的扇区分布有如下好处:
1) 将每个扇区划为6个三角形区域,这样幅值差异将不会引起零序电压的周期性跳变。
2) 当有相位差异的并联逆变器的参考矢量落入同一扇区的不同子扇区时,零序电压差值不发生变化,但当参考电压由于相位差异异步地越过两相邻扇区的边界时,零序电压差值会发生跳变,导致环流的跳变。
3) 参考矢量扇区的判断一般是通过其角度和幅值来实现,角度决定了它所落入的大扇区,而通过大扇区的值结合幅值可以判断小扇区。本文通过将并联逆变器的大扇区判断值同步来实现相位差异引起的零序环流的跳变,大扇区同步之后,结合相应的幅值,再进行小扇区的判断,在跨越不同大扇区时候不再引入环流,但这种方法也有缺陷,当并联逆变器参考矢量相位差异过大时该方法将使影响从逆变器的期望输出。

Figure 5. (a) Division of six subsectors in each sector for eliminating periodical ZSCC jumps caused by the difference in the amplitudes between reference voltages; (b) New division of sectors for eliminating periodical ZSCC jumps caused by the different phases
图5. (a) 每个扇区划分6个扇区消除参考电压幅值差异引起的环流;(b) 新扇区分布,以消除由不同阶段引起的定期ZSCC跳跃
4.2. 抑制环流的恒定直流成分
环流中恒定的直流成分是由于并联逆变器的中点电位不一致导致的,为了消除该成分,提出了如图6所示中性点互联结构,使两逆变器的中点电位保持一致,消除了激励源,抑制环流。
4.3. 抑制剩余的低频环流
如前所述,成对的正、负小矢量产生相同的线电压,但产生不同的零序电压,因此可以通过调整正负小矢量持续时间来抑制剩余的低频环流分量,但由于调整小矢量对中点电位也有影响,环流问题和中点平衡问题耦合使控制更加复杂。本文提出了一种开环的方法,无需解耦,就能同时实现二者的控制。假定有两台逆变器并联,选择其中一台为主逆变器,引入变量y1调整正、负小矢量持续时间来控制并联逆变器的中点电位平衡,获得y1的值后可以根据式(16)计算主逆变器的零序电压,并将其发送给逆变器2,逆变器2引入变量y2调整正、负小矢量持续时间进行零序电压的跟踪,逆变器2产生的零序电压同样根据式(16)计算,y2看为0,得到从逆变器的零序电压,这样计算两逆变器的零序电压差值,为了令该差值为零可以根据式(17)计算y2的所需值。这样就达到从逆变器对主逆变器的零序电压跟踪,从而抑制环流。综合以上三种方法即可对逆变器并联系统中的环流起到良好的抑制效果,且作为开环的算法在实际工程中更加稳定,无需添加任何硬件辅助电路,算法也只是对于传统SVPWM的改进,并不复杂,相较于一些复杂算法更易于实现。
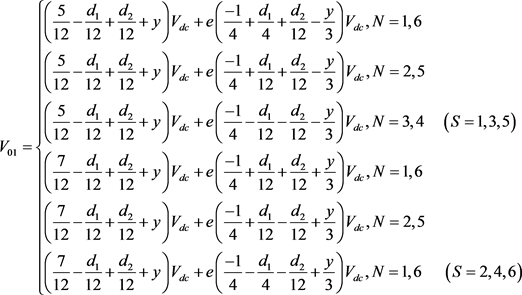 (16)
(16)
 (17)
(17)
5. SIMULINK建模及仿真分析
5.1. 矢量控制系统仿真
Simulink是MATLAB中的一种可视化仿真工具,基于框图设计环境,可以实现系统的动态仿真。在此环境中,不必书写大量代码,而是通过简单连线操作即可实现复杂的仿真模型,图6为文章采用算法的控制模型框架。
5.2. 矢量控制系统仿真
为了确定理论分析的正确性和提出方法的有效性,在MATLAB中搭建了两台T型三电平系统的仿真,对上述所采取的环流控制策略进行验证,实验参数:并联逆变器台数n = 2,桥臂电感L = 1.37 mH,滤波电容Cf = 2 mF,开关频率f = 10 kHz,阻尼电阻R = 1 Ω。直流侧电压为650 V。
图7(a)为两逆变器参考电压幅值差20 V时逆变器的输出,其中ia1为逆变器1的a相输出电流,ia2为逆变器2的a相输出电流,iz为两逆变器间的环流,可以看到环流幅值高达50 A且使输出电流波形畸变。图7(b)是逆变器相位差异5˚时,a相输出电流及环流。可以看到环流幅值达到了40 A,且运行时间越长,输出电流波形畸变越严重。

Figure 7. (a) Inverter output and circulation when amplitude difference is 20 V; (b) Inverter output and circulation when the phase difference is 5˚
图7. (a) 幅值差20 V时逆变器的输出及环流;(b) 相位差5˚时逆变器的输出及环流
图8(a)是两逆变器参考电压幅值相差20 V相位差5˚时,采取文章介绍控制算法,逆变器的a相输出电流及环流,可以看到环流相对于输出电流为极小的值,在图8(b)中放大显示,环流在±0.1 A附近波动,验证了本文控制算法的可行性。
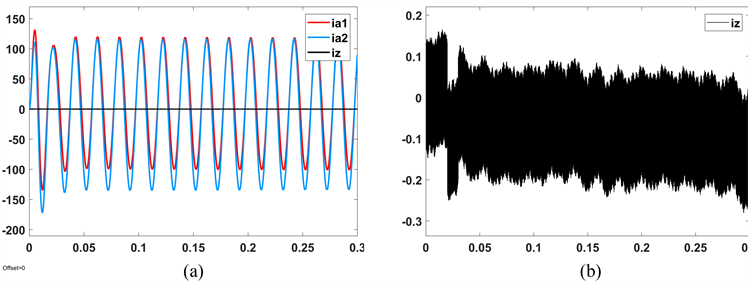
Figure 8. (a) Amplitude difference 20 V phase difference 5˚ control effect; (b) Enlarged circulation
图8. (a) 幅值差异20 V相位差5˚时的控制效果图;(b) 放大显示的环流
6. 结论
本文通过建立基于SVPWM的T型三电平逆变器并联系统的数学模型,分析了零序环流的产生机理,对传统的SVPWM控制策略进行改进,并在MATLAB SIMULINK中仿真验证了该策略的可行性,为实际数字控制系统的设计提供了理论依据。研究表明两台逆变器硬件参数和脉冲的不一致都会导致环流产生,在实际应用中是无法避免的,环流不仅增加系统损耗,还会使逆变器输出波形畸变,无环流控制的逆变器并联系统不能直接使用。而采取本文提出的环流抑制策略后,可以保证系统的稳定运行。相较于现有的环流抑制策略,本文文采用的方法无需增加硬件辅助电路,成本低,且是一种开环的控制方法,相较与闭环算法更加稳定,算法仅是从传统SVPWM改进而来,相较于一些复杂算法更易于实现,在实际工程应用中优势明显。