1. 引言
人才是城市创新和发展的动力,创新人才能够很快地掌握最新的知识和信息,特别是掌握知识生产的能力,以及信息采集、处理、分析、传输与使用能力,这成为了城市取得发展优势的关键。但是,目前我国人才资源结构存在专业结构不合理、行业分布不合理等问题。为此,分析和研究城市就业市场的人才需求对解决人才结构布局不合理、人才的短缺以及城市建设和创新传播等方面具有十分重要的意义。
以往的研究中,许多学者分别对人才发展进行了不同的研究。在国内,2003年,陆晓芳等人 [1] 建立了评价指标体系,运用主成分分析法建立了人才要素区域竞争力的评价模型。2006年,兰艳章等人 [2] 利用熵值法对人才甄选综合评价中的权系数问题进行客观赋值,提出基于熵权值的多层次人才甄选评价法。2008年,胡瑞卿等人 [3] 构造了集“模糊综合测评”和“主成分分析测评”优点于一体的“科技人才合理流动程度的模糊层次主成分分析测评模型”。2010年,黄凤等人 [4] 构建以品质、学识、能力为核心指标的管理型人力资本价值评估指标体系,采用层次分析法和熵值法对管理型人力资本价值进行定量计量。2011年,肖利哲等人 [5] 构建了由基础层、核心层和结果层组成的多方案人才战略决策模型。李健飞等人 [6] 运用劳动经济学、多元统计学、社会学等有关理论,构建了我国不同地区科技人才吸引力评价指标体系及测评模型。2012年,李朋林等人 [7] 运用SVM方法构建了陕西省人才资源与经济增长的关系模型。2013年,杨焕海等人 [8] 提出一种ARIMA-LSSVM的人才需求组合预测模型。2016年,杨璐瑶等人 [9] 研究我国创新型人才发展当前存在的人才培养、选拔、引进、激励等制度问题。2019年,高建祥等人 [10] 研究了城市人才吸引力的评价标准,深入论证了城市各项指标对人才的吸引力影响。在国外,1996年,Horowitz等人 [11] 推导了一个多方程计量经济模型,以确定科学人才的空间分布反过来在区域经济活动中的体现程度。2009年,Faggian A等人 [12] 使用来自110个国家/地区的1569个次国家区域的新建数据库,调查了区域发展的决定因素,提出了一种新的区域发展模型。2011年,An等人 [13] 对区域人才生态环境综合评价体系进行研究。2012年,Xiu-Jun L等人 [14] 总结了区域人才开发战略的定义、内涵与结构、模式和研究水平的主要观点和区域人才开发战略研究中存在的问题。2013年,Martindale R J J等人 [15] 研究了在通过判别函数分析来调查问卷在现实世界中的适用性。2017年,Cadorin E等人 [16] 分析了四个与人才有关的案例,并且证实了科学园区与学生社区的紧密联系以及与具有公认品牌的国际网络的联系的重要性。2011年,Mellander C等人 [17] 围绕着两个核心问题:“有一个如何最好地衡量人力资本的问题”和“关于产生人力资本地域分布的因素”展开了辩论。2015年,HUO Jingbo等人 [18] 建立了人才流入区与流出区之间的不对称演化博弈模型。
本文根据城市发展对人才的需求和A-City的Total demand (Pers.)与Education requirements之间的关系。建立了支持向量机模型预测未来三年A-City潜在的人才需求。并采用客观评价的方法——熵值法赋予各变量权重,建立了人才吸引力的评价模型,计算A-City和上海市的得分来量化评价A-City的人才吸引水平。陆晓芳等人 [1]、胡瑞卿等人 [3]、黄凤等人 [4]、李健飞等人 [6]、高建祥等人 [10]、An等人 [13] 通过建立不同的人才发展评价模型,对城市或区域发展与人才之间的引进做出相应的评价和讨论。但是缺乏对未来人才数量的预测和潜在人才需求的研究。兰艳章等人 [2] 研究了人才的甄选评价,对人才甄选综合评价中的权系数问题进行客观赋值,但却没有解决城市该如何引进人才的问题。肖利哲等人 [5]、李朋林等人 [7]、杨焕海等人 [8]、杨璐瑶等人 [9]、Faggian A等人 [12]、Xiu-Jun L等人 [14]、HUO Jingbo等人 [18] 通过对政策的研究和区域人才引进战略的讨论,建立了相关人才需求组合预测模型,对地区的发展对人才的需求做出了预测。但却忽略了对人才吸引力水平的评价和对潜在人才需求的研究和讨论。没有结合地区的发展对人才需求进一步深入的探讨。对城市就业市场的人才需求进行研究需要从工作需求,预期职业和所需教育背景等方面考虑,对不同职业,不同学历和教育背景的人才分别进行研究和讨论,并预测未来几年内的潜在人才需求。并根据城市现阶段的人才需求和学生就业情况出发,结合城市的刑侦类别和所在地域以及发展情况、发展前景和产业布局、政策规划,对人才的需求作出进一步的讨论和评价。本文建立了支持向量机模型预测未来三年A-City潜在的人才需求。并采用客观评价的方法——熵值法赋予各变量权重,建立了人才吸引力的评价模型,计算A-City和上海市的得分来量化评价A-City的人才吸引水平。从工作需求、预期职业和所需教育背景等方面考虑,对城市就业市场的人才需求建立支持向量机模型,来预测未来三年A-City潜在的人才需求。并结合目前专业人才发展计划中存在的一些问题,提出针对性对策建议,以确保未来市场专业技术人才供需平衡,提升队伍建设水平。
2. 问题分析
本文结合2018年第八届APMCM亚太地区大学生数学建模竞赛B题 [19] 背景和题目所给数据对城市发展与人才需求进行了研究和讨论。并通过建立相关模型对2018年第八届APMCM亚太地区大学生数学建模竞赛B题 [19] 题目进行求解。
1) 根据附件给出的数据进行分析,从工作需求,预期职业和所需教育背景等方面考虑,对城市就业市场的人才需求进行建模与分析。
a) Education requirements指标的分析
所给附件中提供了Total demand (Pers.)的具体人数以及影响Total demand (Pers.)的指标——Education requirements。本文根据其学历要求,将其重新划分分为4个Education requirements指标,即为Above Bachelor degree, Bachelor degree, Below Bachelor degree, Unlimited。具体划分结果如表1所示:

Table 1. Reclassification of education requirements
表1. Education Requirements的重新分类表
b) Sector指标的分析
题目所给的数据中提供了大量的Sector的种类,含有Computer software, Sales management, market/marketing, Sales, Computer hardware等共50种行业。本文根据“ISICRev4.0 2016.9”,将其分为18类,具体的关系如图1所示:
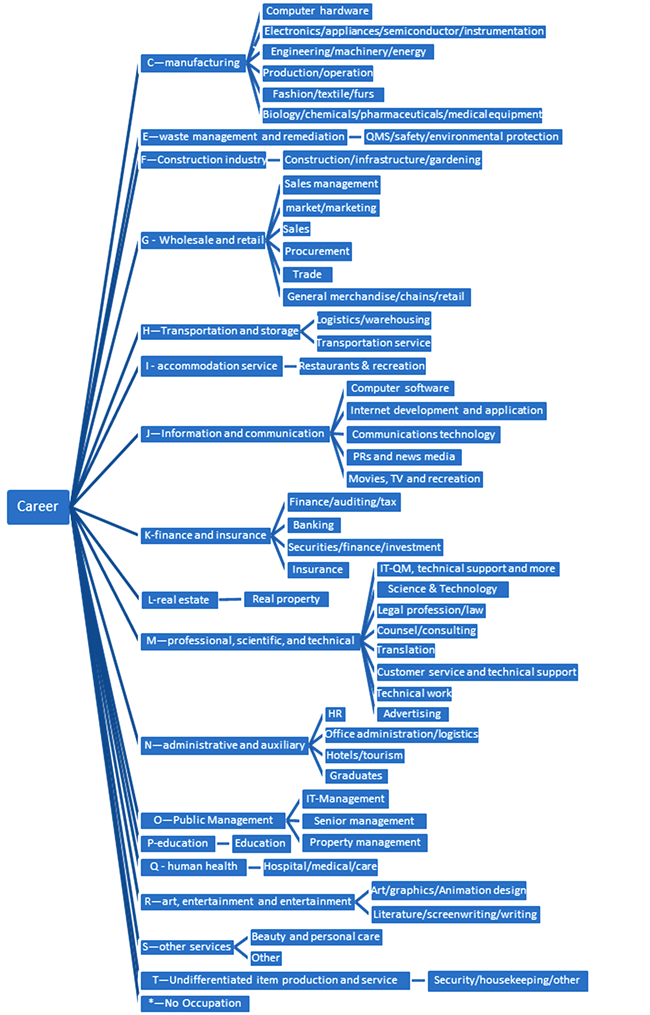
Figure 1. Occupation classification diagram
图1. 职业分类关系图
2) 根据附加数据以及A城市现阶段的人才需求和学生就业情况,建立A市人才需求模型,并预测未来三年的人才需求。
由于人才需求量具有周期性、多元化等特点,为了预测未来三年的潜在人才需求量,本文利用支持向量机(SVM),建立了支持向量机模型,实现了高效的从训练样本到预报样本的推理。
3) 运用问题2中的数据和结论来推断A城的行政类别,可能的地理区域,经济状况和高科技产业发展。
本文结合第一二题中求解的结果。采用最短距离法推测诊断结果,从而可以得到A-City的行政类别,可能的地理区域,经济地位和高科技产业发展。
4) 对如今大学毕业生的就业机会多样化现象进行建模和量化,为A城的发展和人才引进提供策略。
本文选取五个指标,分别是:发展前景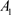 、生活水平
、生活水平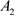 、主要行业增长率
、主要行业增长率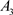 、城市环境
、城市环境 、政策影响
、政策影响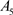 ,建立了人才吸引水平模型。采用克隆巴赫系数来衡量。该系数愈高,各个指标间的信度愈高,即一致性越好。信度只要达到0.70就可接受,介于0.70~0.98均属高信度,而低于0.35则为低信度,必须予以拒绝。
,建立了人才吸引水平模型。采用克隆巴赫系数来衡量。该系数愈高,各个指标间的信度愈高,即一致性越好。信度只要达到0.70就可接受,介于0.70~0.98均属高信度,而低于0.35则为低信度,必须予以拒绝。
本文选取评价模型中的客观赋权法——熵值法,利用熵值法算出的各指标量的权重,再用各指标量与其权重的乘积和计算得分,量化吸引力水平。为了更好、更客观的体现打分的可靠性,选取上海市作为参照。为城市发展和人才引进提供策略。
3. 模型的介绍
3.1. 人才需求PCA数学模型
1) 对原始数据进行标准化处理
由于各指标代表的性质不同,因而其计量单位一般也是不同的。为了消除不同单位的影响,使各个指标具有可比性,以利于主成分的含义解释,通常要对搜集的原始数据进行标准化处理。所以对这Above Bachelor degree, Bachelor degree, Below Bachelor degree, Unlimited四个指标的观测数据矩阵为:
 (1.1.1)
(1.1.1)
其中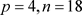 。那么可以对原始数据进行标准化处理:
。那么可以对原始数据进行标准化处理:
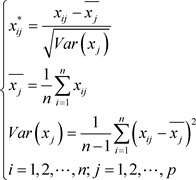 (1.1.2)
(1.1.2)
2) 计算样本相关系数矩阵
假定原始数据标准化后仍然用X表示,则经标准化处理后数据的相关系数为:
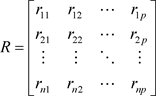 (1.1.3)
(1.1.3)
其中
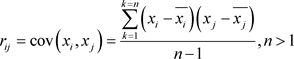 (1.1.4)
(1.1.4)
3) 计算相关系数矩阵R的特征值和相应的特征向量
特征值: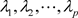 。
。
特征向量: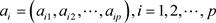
4) 选择重要的主成份,并写出主成份表达式
由主成份分析可以得到p个主成份,但是由于各个主成份的方差是递减的,包含的信息量也是递减的,所以实际分析时,根据贡献率选取前k个主成份。贡献率 指的是某个主成份的方差占全部方差的比重,即Above Bachelor degree, Bachelor degree, Below Bachelor degree, Unlimited所对应的特征值占全部特征值合计的比重:
指的是某个主成份的方差占全部方差的比重,即Above Bachelor degree, Bachelor degree, Below Bachelor degree, Unlimited所对应的特征值占全部特征值合计的比重:
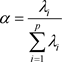 (1.1.5)
(1.1.5)
贡献率 越大,说明该主成份所包含的原始变量的信息越多。
越大,说明该主成份所包含的原始变量的信息越多。
5) 计算主成份得分
根据标准化的原始数据,按照各个样品,分别代入主成份表达式,就可以得到各主成份下的各个样品的新数据,即主成份得分。具体形式如下:
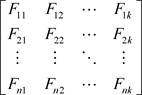 (1.1.6)
(1.1.6)
其中: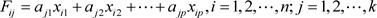 。
。
3.2. 分析预测潜在人才的支持向量机模型
支持向量机最初用于数据分类问题。在数据分类中,对于一组数据寻求一个满足分类要求的超平面,使训练集中的点依照这个平面正确地分为两类,同时使分开的数据点距离分类超平面最远,这便是支持向量机的核心思想。
在图2中,圆和三角形分别代表两类数据,中间虚线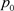 为分类超平面,
为分类超平面, 为其法向量,b为偏置。距离分类超平面最近的样本点为支持向量,过支持向量且平行于分类超平面的平面,称为分类边界,它们之间的距离为分类间隔s。
为其法向量,b为偏置。距离分类超平面最近的样本点为支持向量,过支持向量且平行于分类超平面的平面,称为分类边界,它们之间的距离为分类间隔s。

Figure 2. Schematic diagram of the classification boundary of the support vector machine
图2. 支持向量机的分类边界示意图
假设给定的数据样本集为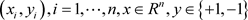 则分类超平面
则分类超平面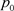 为:
为: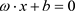 ,分类边界
,分类边界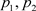 为:
为: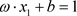 或
或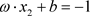 。归一化的样本数据满足:
。归一化的样本数据满足:
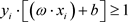 (2.1.1)
(2.1.1)
其中分类间隔为:
 (2.1.2)
(2.1.2)
即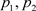 之间的间隔为
之间的间隔为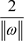 ,寻求最优超平面意味着最大化
,寻求最优超平面意味着最大化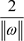 。于是寻求最优超平面的问题转化为求解二次规划的问题:
。于是寻求最优超平面的问题转化为求解二次规划的问题:
 (2.1.3)
(2.1.3)
由于实际的数据集中,数据有的仅近似线性可分甚至非线性可分。对于近似线性可分,允许极少数点不满足以上分类要求,对于这种易被误判的点,加入弱化分类要求的松弛变量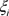 和误判时的惩罚因子C。则原二次规划变为:
和误判时的惩罚因子C。则原二次规划变为:
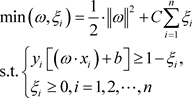 (2.1.4)
(2.1.4)
其中C是一个大于0的常数,可通过参数调优确定。
而在非线性支持向量回归机中,可以通过非线性映射到高维空间,将非线性问题转化为高维空间中的线性或近似线性问题。与分类问题不同,此处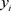 并不限定取−1或1,而是可以取任意实数。即寻找
并不限定取−1或1,而是可以取任意实数。即寻找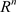 的一个函数
的一个函数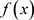 ,使得:
,使得: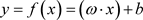 以便用
以便用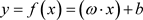 来推断任一输入的值。其中,
来推断任一输入的值。其中,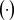 是内积。根据结构风险最小化原则,函数
是内积。根据结构风险最小化原则,函数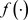 应该使得下式成立:
应该使得下式成立:
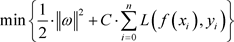 (2.1.5)
(2.1.5)
L为损失函数,通常采用不敏感区损失函数,其形式如下:
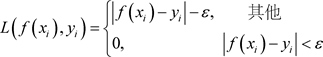 (2.1.6)
(2.1.6)
然后引入松弛变量 和
和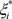 ,则函数可以用如下优化来等价:
,则函数可以用如下优化来等价:
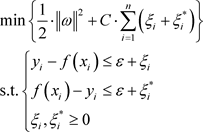 (2.1.7)
(2.1.7)
采用Langrange乘数法解决此约束优化问题,构造Langrange方程:
 (2.1.8)
(2.1.8)
式中,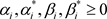 ,为拉格朗日乘数,
,为拉格朗日乘数,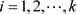 。
。
最终求得回归问题变为:
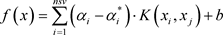 (2.1.9)
(2.1.9)
式中, 为支持向量的个数,
为支持向量的个数, 为对应支持向量的系数;
为对应支持向量的系数; 为阈值。可由任意两个支持向量求解。
为阈值。可由任意两个支持向量求解。
3.3. 判别模型
在问题一中,将Education requirements指标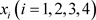 构成Education requirements指标矩阵:
构成Education requirements指标矩阵:
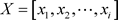 (3.1.1)
(3.1.1)
根据中华人民共和国人力资源和社会保障部中知:各城市岗位空缺与求职人数的关系均值矩阵为:
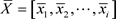 (3.1.2)
(3.1.2)
定义A-City 的 Education requirements指标矩阵与均值之间的欧氏距离为L,则
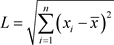 (3.1.3)
(3.1.3)
通过计算机循环运算,找到与样本中欧式距离最短、次短的城市与之匹配,再结合A-City的具体情况的分析,最后确定其可能的地理区域,经济地位和高科技产业发展。
3.4. 人才吸引水平模型
3.4.1. 一致性检验
在人才吸引力评价体系中,各个指标必须从不同的方面反映影响人才吸引力的情况,又不能出现一种指标的重要程度大于另一种指标的重要程度。所以在建立了人才评价体系之后,必须进行各个指标间的一致性检验。对每个一级指标分别进行一致性检验如表2:

Table 2. Consistency test results of various first-level indicators
表2. 各类一级指标的一致性检验结果
根据检验结果来说,发展前景、生活水平、主要行业增长、城市环境、政策影响这五个一级指标可以对于人才吸引这个评价目标而言,能够较为准确的衡量。
3.4.2. 熵值法模型
人才吸引力评价指标体系中,各评价指标从不同方面反映了人才吸引力的影响因素,但它们对人才吸引力的影响力不同。为此,我们选择使用熵值法来确定各项指标在评价体系中所占的权重,从而量化各项指标对人才吸引力的影响程度。
熵值法基本原理:
在信息论中,熵是对不确定性的一种基本度量。信息量越大,不确定性就越小,熵也就越小;信息量越小,不确定性就越大,熵也就越大。我们可以用熵值来衡量某个指标的离散程度,指标离散程度越大,该指标对综合评价的影响越大。
其基本表达式为:
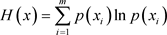 (4.1.1)
(4.1.1)
其中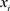 为第i个状态值(共有m个状态),
为第i个状态值(共有m个状态),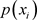 为出现第i个状态值的概率。
为出现第i个状态值的概率。
由于各个指标的量纲不同,所以利用以下公式对各指标值进行非负数化、归一化处理。即取X矩阵中的第i列各元素与该列值最小的元素作差,再取该列值最大元素与该列各元素作差,然后二者作商,最后加1。得到新矩阵R且各元素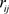 的值处于
的值处于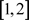 之间。
之间。
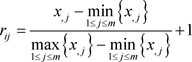 (4.1.2)
(4.1.2)
取R矩阵第i列各元素与该列各元素之和作商,得到P矩阵,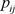 为其中第i行,第j列元素。
为其中第i行,第j列元素。
所以熵值为:
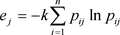 (4.1.3)
(4.1.3)
其中,k为调节系数,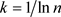 。当确定了参与评价的城市数n,k就是常量。
。当确定了参与评价的城市数n,k就是常量。 ,
,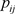 为第
为第 个城市,第j个指标的指标标准化值。
个城市,第j个指标的指标标准化值。
对给定的指标j,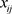 的差异性越小,
的差异性越小,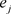 就越大。当
就越大。当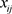 全部相等时,
全部相等时,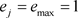 ,此时指标j没有作用,各指标值的差异越大,
,此时指标j没有作用,各指标值的差异越大,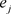 越小,说明该指标起的作用越大。
越小,说明该指标起的作用越大。
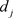 为第j个指标评价值数据的分散程度:
为第j个指标评价值数据的分散程度:
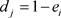 (4.1.4)
(4.1.4)
将评价指标的熵值转化为权重值D
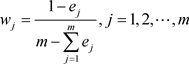 (4.1.5)
(4.1.5)
其中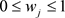 ,
,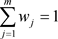 。
。
最后,得出各指标的熵权综合评价值。将各指标的权值与其对应的指标值相 乘并求和,其评价模型为:
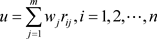 (4.1.6)
(4.1.6)
4. 模型的求解及结果分析
4.1. 问题1PCA数学模型的求解
PCA算法的算法步骤流程图如下图3所示:
PCA算法结果
通过MATLAB编程,本文得出Sector所对应的Total demand (Pers.)与Education requirements的特征值矩阵如表3所示:

Table 3. Eigenvalue matrix of class 18 Sector
表3. 18类Sector的特征值矩阵
以上表格是不同的Sector所对应的Education requirements指标的特征值矩阵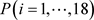 。通过上表可以发现:不同的Education requirements对应的特征值矩阵差异明显,即本文可以通过计算特征值矩阵的相似度来推测城市期望的职业和所需的教育背景。
。通过上表可以发现:不同的Education requirements对应的特征值矩阵差异明显,即本文可以通过计算特征值矩阵的相似度来推测城市期望的职业和所需的教育背景。
4.2. 问题2分析预测潜在人才的支持向量机模型的求解
运用MATLAB编程,采用支持向量机算法,对附件中2015年9月至2018年8月中Total demand (Pers.)的人数拟合建模。再运用滚动预测的思想,求出2018年9月至2021年8月潜在人才的数量,其预测值见表4:

Table 4. Predicted value of potential talent from September 2018 to August 2021
表4. 2018年9月至2021年8月潜在人才的预测值
分析预测潜在人才的支持向量机模型结果的分析
将附件中2015年9月至2018年8月中Total demand (Pers.)的人数拟合建模以及2018年9月至2021年8月导入MATLAB中,可做出基于支持向量机的中国2015年9月~2021年8月潜在人才的预测值与实际值的比较图与2018年9月至2021年8月潜在人才的预测值,如图4、图5所示:
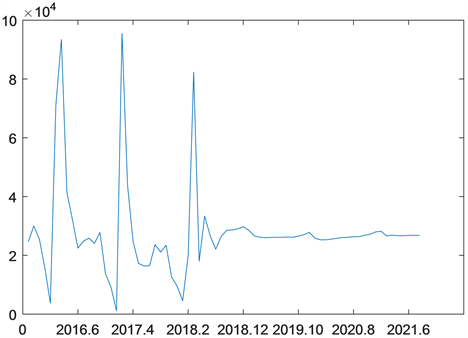
Figure 4. Based on support vector machine, the predicted and actual value of potential talents in China from September 2015 to August 2021
图4. 基于支持向量机的中国2015年9月~2021年8月潜在人才的预测值与实际值
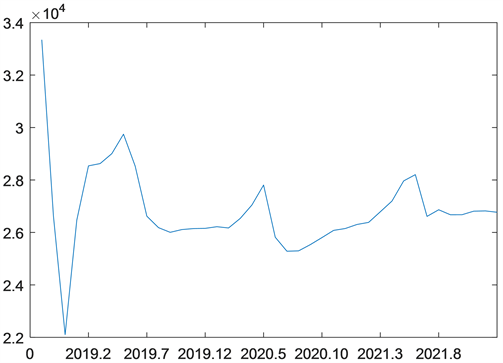
Figure 5. Comparison of actual values and predicted values of potential talents from September 2018 to August 2021
图5. 实际值的比较图与2018年9月至2021年8月潜在人才的预测值
从图4与图5可以看出在开始行业未稳定时Total demand (Pers.)的人数需求是呈周期性变化,但在后面的预测过程中也有一定程度的周期性变化,但变化没有2015年9月~2018年8月剧烈。
4.3. 问题3判别模型的求解
4.3.1. 高科技产业发展判别
首先针对高科技产业发展,本文认为高科技产业发展的基本全都是高文化背景得人,因此本文根据高智商人才在A-City各行业中的分布情况来判断该市的高科技产业发展情况。
对于A-City,总共本科以上学历在各行业中只有503人,占总数的0.346%,所以本文可以判断A-City的高科技产业发展的速率较低。
4.3.2. 与行政类别判别
对于行政类别和经济地位,本文认为一个城市的行政类别与其城市的重要贡献专业人才的类型具有相当大的关系,我们相信一个优秀的城市它的重要贡献人才更偏向于高精尖产业或第一产业。
从附件中给的数据可以体现出A-City的第一产业为G类(wholesale and retail)产业,并不属于高精尖技术,带来的收益也较为低下;所以A-City行政类别和经济地位都不高;其行政类别可能为副省级市或者地级市这两类。
4.3.3. 地理区域判别
首先在问题一中,本文得到18类Sector的特征值矩阵,所以其指标矩阵X可表示成: ,其中
,其中 ,
, 。
。
将18类Sector的特征值矩阵带入得:
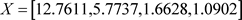
根据中华人民共和国人力资源和社会保障部中知:各地区岗位空缺与求职人数的关系均值矩阵如表5所示:

Table 5. Mean value matrix of job vacancies and job seekers in different regions
表5. 不同地区岗位空缺与求职人数的关系均值矩阵
本文将8类Sector的特征值矩阵的数据输入程序,计算出欧式距离。所得结果为西部地区的关系均值矩阵与X的欧式距离最小,即A-City所处于西部地区。
4.4. 问题4人才吸引水平模型的求解
本文根据清华经管学院互联网发展与治理研究中心发布的数据,建立4类第一指标的权重如表6所示:

Table 6. The weight of each evaluation criterion as a target of evaluation
表6. 各评价标准占评价目标的权重
因为上海数字人才净流入量领跑全国,所以我们本文上海市为基准,对A-City的人才吸引力做出量化评价,即可得出所以可以得到在没有新职业偏好的A-City、有新职业偏好的A-City与上海的综合得分,如表7所示:

Table 7. A-City and Shanghai's comprehensive score sheet
表7. A-City与上海的综合得分表
从表7可以明显的看出,大学生有了一些新的职业偏好,对城市发展产生较大的作用。
5. 策略和建议
随着社会经济的发展,人才越来越显示出其不可替代的作用。科教兴国的人才战略,适应未来经济发展的需要,在人才方面应该从以下几个方面入手:
第一,大力提倡多种形式办学,实现多条腿走路。要实现人才的显著增长,就必须加强高校的人才培养力度,同时大力提倡多种办学形式,加强企业对人才的二次培养以及成人教育,形成公办教育和民办教育共同发展、社会教育和海外教育共同参与的教育培养新格局。近几年,我国的实践也同样可以看出这一点。
第二,在人才投资方面,要树立人才是最重要的资本的理念;制定加大人才投资力度的政策,强化人才资源的超前性投资;实行人才投资多元化政策,建立政府、社会、个人相结合的人才投资回报政策;解决人才投资的动力机制和立法问题;在人才数量增加的同时要注重人才质量的不断提升。
第三,注重高质量人才的引进。人才引进成本低、见效快,是一种便捷的人才资源开发方式。政府应该建立规范的人才引进机制,完善人才市场的管理。同时,加强优惠政策,吸引外部人才的流入和防止人才外流。在引才引智时,应防止和避免盲目引进、重复引进和低效引进。
第四,在人才使用方面,政府要积极营造各种以人为本的环境,包括创业环境、市场环境、生活环境和舆论环境;建立良好的用人机制,防止人才外流;要保持人才政策的相对稳定性,注意政策的配套,谨防牵一发而动全身,导致整个人才系统状态的失衡与振荡;充分发挥人才的作用,以便对该城市经济发展产生巨大的拉动作用。
基金项目
西南科技大学大学生创新基金项目(项目编号:CX19-061)。