摘要:
本文主要利用了MATLAB软件对常用的常微分方程数值解法编程实现,如欧拉法和经典的四阶龙格库塔算法,通过相应的数值算例的结果,分析了两种算法的优缺点。最后我们把算法应用到了一个具体的实例,分别用欧拉法和经典的四阶龙格库塔法进行求解并对计算结果做了比较。
Abstract:
In this paper, we mainly use MATLAB software to program the numerical solution of ordinary differential equation, such as Euler method and classical fourth-order Runge Kutta algorithm. Through the results of corresponding numerical example, we analyze the advantages and disadvantages of these two algorithms. Finally, we apply those algorithms to a concrete example; we solve it and compare the results.
1. 常用的数值算法
常微分方程的理论和方法不仅在自然科学领域中应用非常广泛,而且在社会科学的各个领域有着越来越多的研究。但是很多时候,我们都没办法求出常微分方程的解析解,因而需要用数值算法去求出相应的数值解。常微分方程一般所用的求解初值问题的数值解法简单来说分为两类:单步法和多步法 [1] - [6]。本文主要讨论了单步法中的两类方法。
考虑如下的初值问题:
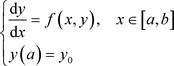
数值算法一般是:取步长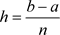 ,将
,将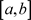 分成n等份,得到离散点
分成n等份,得到离散点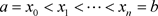 ,进而求解
,进而求解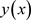 在这些离散点处的近似值
在这些离散点处的近似值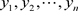 。
。
1.1. 算法介绍
欧拉法的迭代格式为: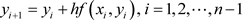 。在已知初值
。在已知初值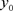 的情况下,我们便可以依次推算出:
的情况下,我们便可以依次推算出:

经典的四阶龙格库塔算法的迭代格式为:
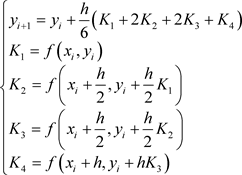
1.2. 数值算例
我们分别用欧拉法和四阶的龙格库塔算法,利用MATLAB软件编程来计算如下的初值问题:
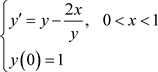
得到结果如表1所示:

Table 1. Comparison of calculation results
表1. 计算结果对比表
从表1可以看出,四阶龙格库塔法在的精确度是要高于欧拉算法的,但是欧拉算法较四阶的龙格库塔算法来说,要更简单。
2. 算法的实际应用
在文献 [7] 中,研究了三维的微生物连续发酵生产1,3丙二醇的微分方程动力系统如下:
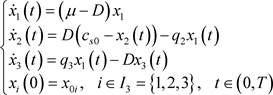
其中: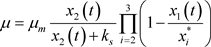 ,
,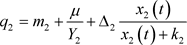 ,
,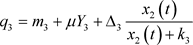 。
。
参数: ,
,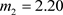 ,
,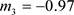 ,
,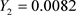 ,
,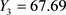 ,
, ,
,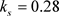 ,
,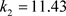 ,
,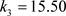 ,
,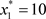 ,
,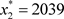 ,
,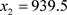 ,
,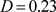 ,
,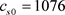 (具体的参数意义可以参见相关文献)。
(具体的参数意义可以参见相关文献)。
我们用欧拉法来求解该系统,建立迭代格式如下:
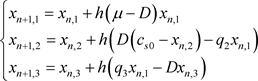
参数为: ,
,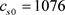 ,
,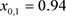 ,
, ,
,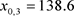 ,步长h取0.01,计算结果如表2所示:
,步长h取0.01,计算结果如表2所示:

Table 2. Calculation results of Euler method
表2. 欧拉法计算结果
我们用四阶的龙格库塔算法来求解该系统,建立迭代格式如下:
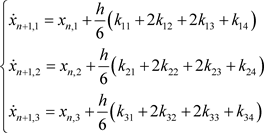
核心代码如下:

计算结果如表3所示:

Table 3. Calculation results of fourth-order classical Runge Kutta algorithm
表3. 四阶经典的龙格库塔算法的计算结果
从两组计算结果可以看出,欧拉法和经典的四阶龙格库塔算法都能够对该系统进行求解,两组数据相差不大。因为系统本身和实验数据都是带有误差的,而且该系统没有解析解,所以没有对两组数据的精确度作对比。
3. 结论
本文主要研究了利用MATLAB软件对欧拉法和经典的四阶龙格库塔算法进行了编程并上机实现,通过数值算例的结果分析了两种数值算法的特点。最后,分别用欧拉算法和经典的龙格库塔算法求解了一个三阶的微分方程动力系统,从计算结果来看,两种方法都适合对该系统的求解。常微分方程的数值算法还有很多,以后会再讨论。
基金项目
沈阳航空航天大学大学生创新创业训练项目,项目编号:201810143271。