1. 引言
随着科学技术的发展,越来越多实际问题显现出非线性的本质,故而非线性问题早已渗透于我们身边的方方面面。对于非线性问题,我们通常转变成非线性方程来解决。而对于非线性方程的求解,不像线性问题可以用线性叠加原理来求解。非线性问题求解起来相对比较复杂,而对于此问题,国内外专家学者近年来也进行了诸多研究。对于强非线性系统的定量分析方法主要有L-P摄动法 [1] 、同伦分析方法 [2] [3] [4] [5] 、双曲函数摄动法 [6] 等。
廖世俊教授于1998年首次提出同伦分析方法,并将其应用到非线性振动的研究中 [7] [8],文献 [9] 给出非线性单自由度振动系统的两个周期公式,该公式对系统任何的振幅都是一致有效的。廖世俊等学者 [10] 应用同伦分析方法,举例并分析研究了非牛顿磁流体流动系统的解析解。钱有华等人 [11] 对同伦分析方法进行了改造,得到一类强非线性耦合van der Pol-Duffing系统的解析近似周期解。2016年,崔继峰 [12] 利用同伦分析方法并结合多尺度思想,对受迫van der Pol-Duffing振子的周期解等性质进行了研究。2016年,许天亮等人 [13] 利用同伦分析方法研究了几类简单非线性微分方程问题,并验证了同伦分析方法在求解部分非线性微分方程的优越性。2017年,郭江明 [14] 用同伦分析方法探究了带有时滞的耦合van der Pol系统双Hopf分岔和周期解。2018年,杨孟 [15] 等学者采用同伦分析方法研究了圆盘上非牛顿幂律流体的Marangoni边界层流动传热问题,利用求解化简后的非线性问题,从而获得一系列的近似解析解。
耦合van der Pol方程也是社会诸多学者研究的一个热点问题,其在动力学性质方面取得许多显著的成果。2007年,Rompala Kevin等 [16] 基于3-DOF耦合van der Pol系统,研究系统的动态行为。2009年,Jiashi Tang等 [17] 研究了对耦合van der Pol极限环的振幅进行控制的有效方法,并分析了部分弱非线性系统,得出了控制参数同振幅之间的关系,为如何有效控制振幅提出有效建议。同年,钱有华等 [18] 巧妙利用同伦分析方法探究了参数激励的非自制薄板系统的周期解。2016年,吴俊 [19] 利用KAM理论分析证明拟合周期解存在于2-DOF耦合van der Pol方程中。2018年,石兆羽等 [20] 利用混沌振子对微弱信号敏感以及对强噪声具有良好免疫力的特性,提出基于耦合van der Pol-Duffing振子系统检测微弱信号的新方法。2019年,施添添等 [21] 通过讨论特征方程根分布情况研究含时滞的大规模van der Pol-Duffing耦合振子系统的同步和异步周期振荡、概周期运动以及混沌吸引子等非线性动力学现象。
本文研究的耦合van der Pol振子环结构如图1所示 [22] [23]。而环状结构在医学、光学、电路、机电传感器和神经网络等诸多领域有着重要的应用。2007年,Fuad,Baolong Lu和Surendra Singh [24] 研究了带调制泵的双向固态环形激光器的准同步、同步和非同步混沌振荡的机制,并用最大李亚普诺夫指数进行了计算。2010年,Fernando,Ana Paula和Carla [25] 研究了由两个(单向或双向)环形细胞通过缓冲细胞耦合而成的耦合细胞网络的动力学特性。2016年,Faralli [26] 等人论证了在具有母线和环形拓扑结构的光子集成片上网络中,在同一微环中添加或删除两个波长相同的光信号的可行性。2019年,Xu,Yu和Wang [27] 为了避免简单环拓扑结构的缺点,提出了一种具有时延的耦合双环网络。采用分治算法分析相邻矩阵特征值的分布研究了周期动力学平衡和层间同步的稳定性,并进一步分析了耦合环与反射波之间的动力学相互作用。
本文主要建立三自由度耦合van der Pol振子环的精确近似解析解,且利用此系统的周期解证明了同伦分析方法的有效性和巨大的应用潜力。此外,还对同伦分析方法和数值积分法的计算结果进行了比较。结果表明,在时间历程图中,即使时间t的值在很大的区间内变化,同伦分析方法的解析解与数值积分解也能很好地吻合。
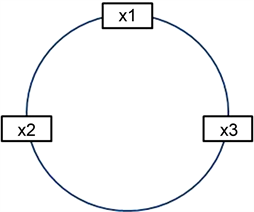
Figure 1. The ring of three-degree-of-freedom van der Pol oscillators with coupled
图1. 耦合三自由度van der Pol振子环
2. 同伦分析方法简述
我们先引入多自由度耦合振子的一般表达式:
(2-1)
其中q为n维未知向量,即
,且
为q关于时间变量t的二阶微分,类似地,
为q关于时间变量t的一阶微分,M,G,K为n阶方阵,而耦合项
则是关于变量
的向量值函数。
首先,我们先引入一个非线性算子:
(2-2)
其中
(2-3)
(2-4)
(2-5)
而这里的
是未知向量函数,r和t分别是空间与时间变量。
由同伦分析方法可知,我们需要构造一零阶形变方程
(2-6)
其中
为嵌入变量,L为辅助线性算子,
为初始猜测解,而h和
分别为辅助参数和辅助函数。辅助参数h对级数解的收敛性有决定性作用,故我们可画出h-ω曲线来确定h的值来确保级数解收敛。
易知,当
时,零阶形变方程(2-6)演变为
;而当
时,(2-6)又可化简为
。所以我们可得出结论:当嵌入变量p由
的变化过程中,解
从初始猜测解
变化到精确解
。
记
(2-7)
我们把
展开成关于嵌入变量p的Taylor级数,可得
(2-8)
若选取适当的辅助线性算子L,辅助参数h和辅助函数
,再结合有效的初始猜测解便可使得幂级数(2-8)在
时收敛,因而可得
(2-9)
向量
定义为
(2-10)
我们对零阶形变方程(2-6)关于嵌入变量p求m次导数,再将求导得到的式子左右两边同除以
,并令
,则我们就可得到m阶形变方程
(2-11)
其中
(2-12)
且
(2-13)
原则上m阶形变方程是线性的,而对于线性问题我们可借助数学软件如Mathematica求解。
3. 同伦分析方法的应用
本论文所研究的系统是三自由度耦合van der Pol方程,其一般表达式为
(3-1)
其中
互为耦合项。对于上述所给的一般方程,我们不妨规定
,
,
,而对于方程(3-1)中
的取值,我们将根据振子运动模式分成四类来讨论 [28] :第一,所有振子都同步运动;第二,两个振子同步运动,而第三个振子以一无关的方式运动(除它与第二个振子有相同周期的振动外);第三,环上相邻的振子之间彼此都相位差1/3周期的运动;第四,两个振子相位差1/2周期,而第三个振子2倍于它们的频率振动。我们将针对上述的四种振子不同的运动状态研究系统的周期解问题。在文章最后,我们会采用数值模拟的形式对其进行验证,表明改进的同伦分析方法作用于此类系统是可取的,并希望该方法在其他科学领域能得到广泛应用。
要解决上述问题,我们先考虑如下的三自由度非线性耦合van der Pol振子:
(3-2)
其中
为关于变量t的二阶微分,
为关于变量t的一阶微分,
为关于变量t的未知实函数,
是耦合项
为已知实参数。
我们设该系统的周期解频率为
,然后引入一个新变量
,将该新变量代入系统(3-2),得到
(3-3)
方程满足初始条件
(3-4)
其中导数表示对变量
微分。
若系统(3-3)的周期解可以用基函数
表示,则有
(3-5)
我们可以假定初始猜测解可表示为以下形式
(3-6)
之后,我们还需要引入辅助线性算子
(3-7)
线性算子L满足下列性质
(3-8)
对于系统(3-2),我们再定义非线性算子
不妨令
,则可得零阶形变方程为
(3-9)
上式满足初始条件
(3-10)
显然,我们很容易得到当
时,方程(3-9)满足初始条件(3-10)的解为
(3-11)
而当
时,满足初始条件(3-10)的零阶形变方程(3-9)与满足初始条件(3-4)的系统(3-3)是等价的,因而有
(3-12)
由此可见当嵌入变量p从0变化到1时,
从初始猜测解
变化到未知的精确解
。类似地,我们也可以得出
从初始猜测频率
往物理变化频率
变化的结论。
我们把
与
都展开成关于p的麦克劳林级数,可得到
(3-13)
其中
(3-14)
通过选取适当的h,我们可以使(3-13)式中的幂级数在
时收敛。那么,结合(3-12)式与(3-13)式,我们可以得到方程的级数解为
(3-15)
记
(3-16)
同样地,我们对零阶形变方程(3-9)关于嵌入变量p求m次导数,再将求导得到的式子左右两边同除以
,并令
,则我们就可得到m阶形变方程
(3-17)
其中
(3-18)
此m阶形变方程满足以下初始条件
(3-19)
由线性算子L的定义与解的表达原则可知,方程(3-17)的等式右边项里不能含有
与
,也不能含有久期项
与
。
我们把这些项都找出来,且令这些项的系数都为0,则可得
(3-20)
其中
(3-21)
且
(3-22)
根据(3-17)和(3-20)式,我们可以求出
的值。为使解的精度更高,我们需要对w进行一定程度的修正
其中v为小参数。
4. 数值模拟与讨论
为了验证同伦分析方法应用于非线性多自由度系统的正确性和有效性,针对耦合van der Pol系统(3-2),我们将分四种情形对其数值模拟进行讨论,并对分别对这四种情形下的理论结果与数值结果进行比较。而耦合项
的取值可借鉴文献 [29] [30]。
4.1. 所有振子都同步运动
令
(4-1)
我们取
,且令
的初始猜测值分别为
,我们需要选取合适的收敛控制参数h来确保级数解的收敛。为此,我们给出了图2所示的ω-h曲线来确定h的取值范围。细观图2可知,当
时,级数解
是收敛的。为简便起见,我们取
,图3和图4分别给出了八阶近似相图和时间历程曲线。

Figure 2.The eighth-order approximation of versus is obtained for
and
图2.
时的八阶ω-h近似曲线

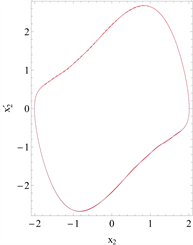


Figure 3. Comparison of the phase curves of the eighth-order approximation with the numerical integration solution is given for
and
图3.
时的八阶近似相图与数值积分法的比较
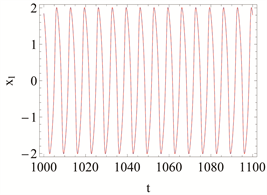

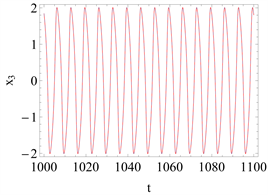

Figure 4. Comparison of the time history responses of the eighth-order approximation with the numerical integration solution is given when
and
图4.
时的八阶时间历程曲线
利用相图(图3)与时间历程图(图4)可证明同伦分析方法求得的相图与数值分析方法所求得的相图结果比较吻合,且能明显看出
三个振子同步运动。其中初始条件为:
根据文献 [31] 并且可求得
的八阶近似表达式为
4.2. 两个振子同步运动,而第三个振子以一无关的方式运动(除它与第二个振子有相同周期地振动外)
令
(4-2)
在此情况中,我们取和情形4.1一样的参数值,即
,
的初始猜测值取为
,我们可以从图5中确定出h的取值范围来确保级数解的收敛。因为h的取值范围为
,为简便起见故仍然取
,一阶近似相图与时间历程图如图6与图7所示。

Figure 5. The first-order approximation of ω versus h is obtained for
and
图5.
时一阶ω-h近似曲线
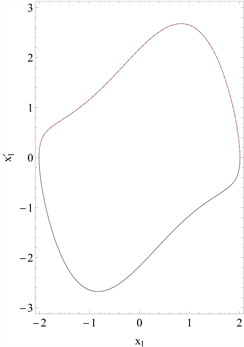
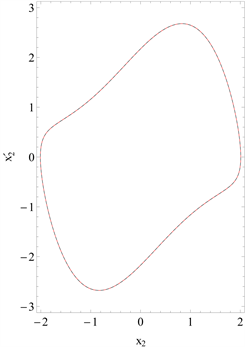


Figure 6. Comparison of the phase curves of the first-order approximation with the numerical integration solution is given for
and
图6.
时的一阶近似相图与数值积分法的比较
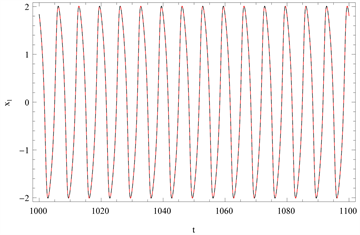

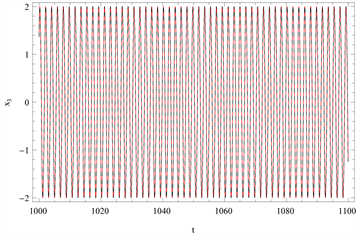

Figure 7. Comparison of the time history responses of the first-order approximation with the numerical integration solution is given when
and
图7.
时的一阶时间历程曲线
利用相图(图6)与时间历程图(图7)可证明同伦分析方法求得的相图与数值分析方法所求得的相图结果比较吻合。观察图7可发现,振子
与
同步运动,而第三个振子
则以一种无关于前两个振子的方式运动。其初始条件为
,且可得
近似表达式为:
4.3. 环上相邻的振子之间彼此都相位差1/3周期的运动
令
(4-3)
在此情况中,环上相邻的振子之间彼此都相位差 周期的运动,因而对系统(3-1)中的各系数取值与前两种情况有所不同。这里我们取
。同样地,初始猜测值也被赋予一些新的数值,
。为确保级数解的收敛,我们取
,从而得到相应地相图与时间历程图(见图8与图9)。




Figure 8. Comparison of the phase curves of the first-order approximation with the numerical integration solution is given for
and
图8.
时的一阶近似相图与数值积分法的比较
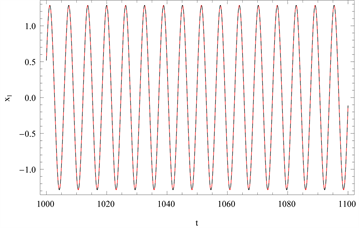
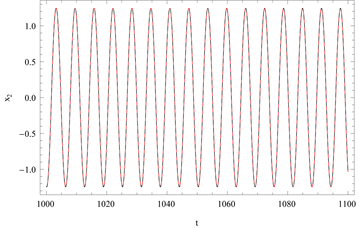


Figure 9. Comparison of the time history responses of the first-order approximation with the numerical integration solution is given for
and
图9.
时的一阶时间历程曲线


Figure 10. Comparison of time history diagrams of
and
in the same condition
图10.
在同一条件下时间历程图的比较
由图8可知,利用同伦分析方法求得的近似解与数值积分法求得的解基本吻合,而由图10也可看出三个振子正相差1/3周期运动。我们同样可求得数值积分法的初始条件为
。
我们也就能得到
与
的近似解表达式:
4.4. 两个振子相位差1/2周期,而第三个振子2倍于它们的频率振动
令
(4-4)
此时,两个振子相位差1/2周期,而第三个振子 倍于它们的频率振动。为计算方便,我们取
,
而初始猜测值求得为
。取
得近似解的相图和时间历程图如图11与图12所示。
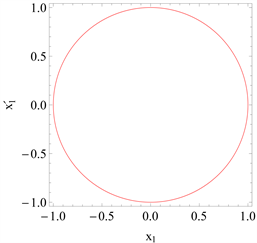


Figure 11. Comparison of the phase curves of the first-order approximation with the numerical integration solution is given for
图11.
时的一阶近似相图

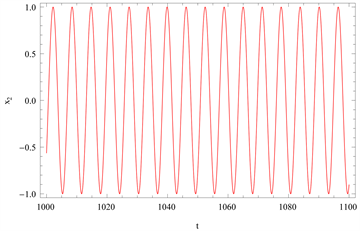
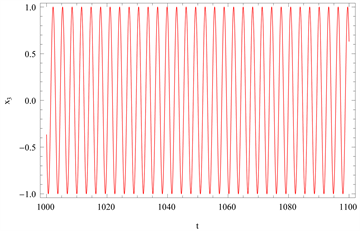
Figure 12. Comparison of the time history responses of the first-order approximation with the numerical integration solution is given for
and
图12.
时的一阶近似时间历程曲线


Figure 13. Comparison of time history diagrams of
and
in the same condition
图13.
在同一条件下时间历程图的比较
通过观察与计算可知,利用同伦法得到的相图与时间历程曲线是合适的,再次证明了同伦分析方法于耦合多自由度振子环系统上的适用性。其数值积分法满足的初始条件为
。
同样地,得到
和频率
的一阶近似解为:
显然,此近似解就是满足条件(4-4)的系统(3-1)的精确解,也符合第四种情况的振子运动(见图13)。
5. 结论
本文利用该方法对多自由度耦合van der Pol振子环进行了精确的近似分析。由之前的数值模拟可以知道,利用同伦分析方法求解三自由度耦合van der Pol方程得到的周期解比较精确。该方法不仅可以计算任意阶次的频率和位移,而且计算量小。与经典摄动技术相比,该方法不需要依靠小参数并可以很好地保证级数解的收敛性以及解的精度,在解决非线性问题方面具有非常好的效果。在后续研究中,我们可以考虑四种不同情况中的振子如何才能互相转换,在何种外激励下使系统形成四稳态局面。
致谢
感谢国家自然科学基金项目(11572288)、浙江省自然科学基金项目(LY20A020003)和浙江师范大学数计学院重点项目(ZD01201713)资助。
NOTES
*通讯作者。