基于供喷平衡的高压油管压力控制

Pressure Control of High Pressure Oil Pipe Based on Balance of Supply and Injection

摘要: 燃油进入和喷出高压油管是许多燃油发动机工作的基础，其间歇性的工作过程会导致高压油管内压力变化，使得所喷出的燃油量出现偏差，从而影响发动机的工作效率。因此，如何保证高压油管内压力稳定成为燃油发动机发展的重中之重。本文提出一种通过控制供油量和喷油量达到质量守恒实现供喷动态平衡的方法，从而保证高压油管内压力尽可能稳定；建立了一种基于供喷平衡的高压油管压力控制质量流量守恒模型，找寻与确定高压油泵内凸轮轴角速度，计算供油周期和喷油周期，以此实现高压油管压力控制；最后本文对所建立高压油管模型进行了整体评价。

Abstract: The high-pressure fuel pipe is the basis of many fuel engines. The intermittent working process will lead to the pressure change in the high-pressure fuel pipe, resulting in the deviation of the amount of fuel injected, thus affecting the working efficiency of the engine. Therefore, how to ensure the stability of the pressure in the high-pressure oil pipe has become the top priority of the fuel engine development. In this paper, a method of achieving dynamic balance of supply and injection by controlling the quantity of oil and injection to achieve mass conservation is proposed, so as to ensure the pressure in the high-pressure oil pipe to be as stable as possible. By establishing a mass flow conservation model of pressure control in the high-pressure oil pipe, the angular velocity of camshaft in the high-pressure oil pump is found and determined, and the oil supply cycle and injection cycle are calculated, so as to achieve pressure control in the high-pressure oil pipe. At last, this paper evaluates the model of high pressure tubing.

1. 引言

燃油进入和喷出高压油管是许多燃油发动机工作的基础，燃油经过高压油泵从供油管进入高压油管，再由喷油嘴喷出。燃油进入和喷出的间歇性工作过程会导致高压油管内的压力变化，使得所喷出的燃油量出现偏差，高压油管内的压力控制成为衡量燃油发动机质量的重要指标，其直接影响着发动机的工作效率。

2. 研究背景

随着发动机控制技术的发展，喷油过程的可控程度越来越高。发动机连续运行过程中管路中燃油压力、流速都会发生瞬变，从而造成喷油压力及喷油量的波动，不利于对喷油规律的精确控制。喷油器与高压油管连通，喷油压力在很大程度上受高压油管的影响，因此压力控制控制技术也一直是国内外研发的重点和难点。北京交通大学的刘峰将CT-FUEL和CT-POWER的程序帮合，构成了共轨式柴油机整机的计算程序，通过改变高压油泵长度、直径，喷油器喷孔直径、针阀弹簧刚度、预紧力等结构参数和高压油管供油脉宽、提前角、喷油次数等运行参数，对管内压力波动幅值进行对比分析，认为高压油管长度最佳值在450 mm至500 mm之间，喷孔最佳直径在化1.5 mm至化2 mm之间，喷油脉宽最佳范围为1.5 ms至2.5 ms，喷油器弹簧刚度及预紧力对油管内压力波动影响较小。集美大学的王永坚等人采用Matlab/Simulink软件平台搭建柴油机共轨燃油系统仿真模型，分析油管内压力波动的影响。武汉科技大学的张光德等人建立低压共轨系统仿真模型，分析共轨管结构参数及供油压力对轨内压力建立时间和共轨管压力波动的影响，并对二甲酸和柴油两种燃油的轨压特性进行了对比。

3. 高压油管压力调控主要部件数学模型

如图1所示，在实际工作过程中，高压油管A处的燃油来自高压油泵的柱塞腔出口，喷油由喷油嘴的针阀控制，即总容积 = 高压油管容积 + 供油管容积 + 柱塞腔容积。由于凸轮转动导致柱塞腔容积变化、总容积变化，使得供油压力不定，需要宏观上控制体积来确定燃油密度，建立质量流量守恒模型，用凸轮角速度控制，以实现高压油管内的压力稳定。因此，在建立高压油管压力调控模型前，应先建立其主要部件数学模型 [1] [2]。

Figure 1. High pressure tubing model in actual working process

图1. 实际工作过程中高压油管模型

3.1. 高压油泵数学模型

高压油泵作用过程主要依靠凸轮轴驱动柱塞，以此改变柱塞腔体积，当柱塞腔内燃油压力大于油管内压力时，出油阀开启，燃油进入高压油管，针对其工作过程在高压油泵柱塞压油过程中，凸轮驱动柱塞上下运动，求解柱塞运动的最大距离L为：

$r_{\max }-r_{\min }=L_z$

当柱塞运动到上止点位置时，柱塞腔残余容积为 $V_{余}$，求得高压油泵总容积：

$V_z=L_z{A}_z+V_{余}$

燃油的压力变化量与密度变化量成正比且比例系数为 $E/\rho$，即：

$\frac{\Delta P}{\Delta \rho }=\frac{E}{\rho }$

当油管内压力为稳定值时，利用最小二乘法对燃油的实验数据运用Matlab软件进行差值拟合得到压力与弹性模量 的关系本文中取燃油密度 $\rho$ 为0.850 mg/mm³得其关系如下：

$E=0.02893P^2+3.0765P+1571.5$

经与实验值检验，压力和弹性模型的拟合程度高，如图2；

Figure 2. Fitting curve of P and E

图2. P与E的拟合曲线

根据的压力与弹性模量的关系：当柱塞运动到下止点位置时，低压燃油会充满柱塞腔，根据此时低压燃油的压力可得该状态下低压燃油密度 $\rho$，依照质量守恒低压燃油充满柱塞腔时的质量，进而求得高压油泵的供油量：

$m_z=\rho V_z$

3.2. 喷油嘴针阀运动模型

喷油阀能够控制高压油管内燃油喷出，喷油针阀抬起前，针阀截面与喷油嘴内壁圆锥面密合，防止燃油流出；随针阀升程增加，燃油可从针阀与内壁空隙喷出，喷油嘴开启面积不同继而影响单位时间内喷油量大小；当针阀升程增加使得空隙可通过燃油的截面积等于喷孔面积，喷油面积恒定为喷孔面积。

针阀升程为0时，针阀截面到圆锥尖的距离 $h_0=D/\left(2\tan 9^{\circ }\right)$。

当针阀升程大于0时，针阀开启，燃油向喷孔流动，此时空隙可通过燃油的截面积小于喷孔面积，流量通过截面以空隙面积为准，公式如下：

$A_2=\pi {\left[\left(h_1+h_0\right)\tan 9^{\circ }\right]}^2-\pi {\left(\frac{D}{2}\right)}^2$

$Q_{bm}={\rho }_0{A}_{21}=\rho C{A}_2\sqrt{\frac{2P_0}{{\rho }_0}}$

当空隙可通过燃油的截面积大于喷孔面积，流量所通过截面以喷孔面积为准，建立方程如下：

$A_2=\pi {\left(\frac{D}{2}\right)}^2$

$Q_{bm}=\rho C{A}_2\sqrt{\frac{2P_0}{{\rho }_0}}$

根据针阀升程与时间的关系，可得流量通过截面积利用时间与截面积变化的曲线，进而求得一周期内的喷油量。

4. 高压油管内压力调控

高压油管工作的先决条件即保证经由供油管进入的燃油和喷油量达到质量守恒，基于高压油管的工作假设，可不考虑高压油管内的液体流动现象，但高压油泵和喷油器的脉动供油和喷油仍导致高压管路中的压力波动 [3]。高压油泵在入口处提供恒定压力，且高压油管内有一定初始压力，通过交替改变供油管入口和喷油管喷出口的边界条件，模拟高压油管内供油、喷油过程，从而达到供喷动态平衡。

4.1. 基于高压油管工作的基本假设

目前市面上广泛应用的高压油管的相关结构参数、承载的工作压力等信息均可参考其规格及型号，本文针对高压油管工作过程中的详细情况，在不影响实际应用的前提下，对系统中某些影响较小的因素进行简化，基于高压油管正常使用情况作出如下假设：

1) 由于燃油内部变化过程极快，忽略燃油物性变化时的热量传递；

2) 忽略高压油管内的液体运动中延程阻力的影响；

3) 忽略高压油管中各部件的弹性形变；

4) 假设柱塞腔内燃油无泄漏且不回流到低压回路。

4.2. 供喷平衡下的压力调控数学模型

当供油量与喷油量达到动态平衡时，遵循质量守恒定律，由于高压油泵每次实际供油时间较短，使得多次供油质量之和等于喷油质量，方程如下：

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{m}_i}=m_b$

喷油嘴未打开前，供油存在递归关系可得下列方程：

$m_i+{\rho }_{i-1}{V}_0={\rho }_i{V}_0$

其中， $m_i$ 为第i次供油后高压油管内燃油质量，单位为mg； $V_0$ 为高压油管内燃油体积，单位为mm³。

控制燃油进出时，压力波动为脉冲形式，以高压油泵供油入口处压力值、高压油管内部压力值和喷油嘴边界压力值为边界条件，经过多个喷油周期可得高压油管内压力稳定值 [4]。在此基础上可建立流入流出质量守恒方程：

${\rho }_{z}C{A}_1\sqrt{\frac{2\left(P_z-P_0\right)}{{\rho }_z}}=\frac{2\pi }{w{T}_b}{\rho }_{0}C{A}_2\sqrt{\frac{2P_0}{{\rho }_0}}$

柱塞内部流量守恒方程(当柱塞腔的压力大于高压油管内的压力时)：

$Q_z=\frac{V_z}{E}\cdot \frac{\text{d}{P}_z}{\text{d}t}+C{A}_1\sqrt{\frac{2\left(P_z-P_0\right)}{{\rho }_z}}$

将上述方程在一个供油周期内积分，并进一步分析计算即得到如下方程式：

$M_z=\frac{V_z}{E}\cdot P_z\cdot {\rho }_z+{\rho }_{z}C{A}_1\sqrt{\frac{2\left(P_z-P_0\right)}{{\rho }_z}}$

上式表明，在基于喷油器工作频率、高压油管尺寸等参数可知情况下，通过该方程即可计算高压油泵供油及喷油针阀的实际正常工作状态所需要的凸轮轴角速度，以此可实现高压油管内的压力调控。

4.3. 模型检验

为确保该模型的实用性，本文通过Matlab对高压油管供喷过程进行模拟计算 [5]，设计程序流程如图3，以此检验该数学模型的准确性。

基于目前高压油管控制研究成果 [6]，参数设定高压油管的内腔长度为500 mm，内直径为10 mm，喷油器每秒工作10次，每次工作时喷油时间为2.4 ms，一周期内的喷油量为34.67 mg，使高压油管内的压力尽量稳定在100 MPa左右。柱塞腔内直径为5 mm，柱塞运动到上止点位置时，柱塞腔残余容积为20 mm³。柱塞运动到下止点时，低压燃油会充满柱塞腔(包括残余容积)，低压燃油的压力为0.5 MPa。喷油器喷嘴针阀直径为2.5 mm、密封座是半角为9˚的圆锥，最下端喷孔的直径为1.4 mm。凸轮极角和极径的关系设定如图4所示。

利用Matlab对本文所建立供喷平衡数学模型求解，使高压油管内的压力尽量稳定在100 MPa左右的凸轮角速度为0.03176 rad/ms。而利用仿真模型求得实验值为知供油周期T = 197.662 ms。由角速度与周期的关系可求得，凸轮角速度为0.03179 rad/ms。该结果与建立供喷平衡模型所求的结果差距较小，证明该模型真实可靠。

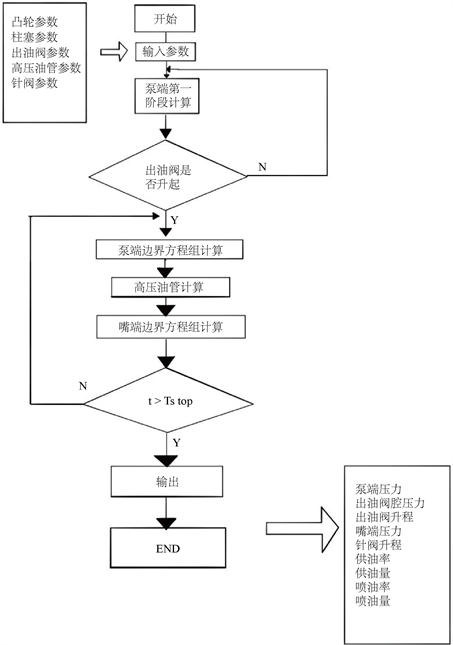
Figure 3. Flow chart of Matlab simulation calculation program

图3. Matlab模拟计算程序流程图

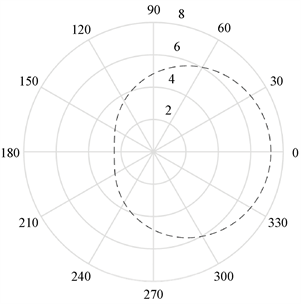
Figure 4. Cam model of high pressure oil pump

图4. 高压油泵凸轮模型

4.4. 符号说明

表1列出了本文所需符号，其他符号，已在文中出现时在进行说明。

Table 1. Symbolic explanation

表1. 符号说明

5. 模型的评价与意义

本文分析了柱塞和凸轮转动的关系，将高压油泵内变化的压力转变为高压油泵内的燃油密度变化，利用凸轮转动引发系统体积变化与燃油密度相联系，转变为用凸轮角速度、极径和燃油体积、密度保证质量流量守恒，以此实现了高压油管内的压力调控。经实验数据与仿真结果拟合检验，该模型计算所得供油周期与仿真结果拟合程度高，能够通过供油周期的控制实现高压油管内的压力调控，因此该模型具备良好的可实施性及一定的工程实用价值。