1. 引言
随着国内经济的快速发展,新技术和新材料的普及更加广泛,其中以施工简单,造价便宜和强度较高为优点的梁则在工业、桥梁、土木等方面得到了极为广泛的应用。为了保证梁结构的安全以及实现其长时间的稳定工作,必须考虑其横振动所带来的影响,以此可以减少不必要的损失。
梁发生横振动时,由于出现了切应力和挠矩,方程出现四阶导数项,边界条件也要相应的增加。若梁的两端固定,且端点的挠矩为零,即端点与支架是铰接性联接,致使端点可以自由旋转但没有位移。设初始位移和初始速度分别为
和
,则梁横振动问题归结为(参见 [1] )求解如下非稳态四阶线性偏微分方程的初边值问题
(1.1)
其中,l为梁的长度,a是与梁的体密度、梁的横截面积以及抗弯刚度有关的一个正常数。
当今,科学计算已成为各类自然学科和技术与工程科学的有效工具,因为在这些领域中的问题通常是以偏微分方程(组)来刻画的,对其求解特别是稳定高效的数值方法是科学计算的主旋律。众所周知有限元方法,谱方法和有限差分方法(有限体积法)是求解偏微分方程(组)的有效数值方法。对简支梁横振动(四阶)问题,其有限元方法需要使用三次样条函数,这会增加计算量但未必带来高阶精度。需指出的是作者在偏微分方程的有限元方法特别是自适应有限元方法方面做了一系列的工作,参看文献 [2] [3] [4] [5]。由于有限差分方法具有结构简单,灵活等特点,广泛受到欢迎。
自从D. J. Evans和A. R. B. Abdullah [6] 建立求解抛物型方程的交替分组显式格式以来,越来越多的文章专注于四阶偏微分方程的有限差分方法:2008年崔嵬 [7] 以求解四阶抛物型方程问题为背景,建立了一个区域分裂并行差分格式,讨论了该差分格式的稳定性和收敛性,证明了当网比
时,该差分格式稳定且收敛;2004年刘胜利 [8] 针对四阶抛物方程的并行化问题,采用三层交替技术实现了有限差分方法,得到的差分格式的截断误差为
;2007冯青华 [9] 给出了关于求解四阶抛物方程的一类具有并行本性的交替分组方法,证明了格式的稳定性;2008年郭阁阳、刘播 [10] 给出了四阶抛物方程的一类变步长本性并行差分格式;2013年武文佳 [11] 以一类二维半线性椭圆边值问题为模型,建立了适用于各向异性网格的四阶紧致有限差分格式,证明了构造的差分格式具有四阶精度;陈世平在 [12] [13] 中构造了一个显格式和隐格式,其局部截断误差为
,后又在 [14] 中,建立了两类新的、具三对角线型系数矩阵的能用追赶法求解的三层隐式差分格式;邓世武等于2015年 [15] 提出了一种曲面重构方法。
在这篇文章中,考虑简支梁的横振动方程的有限差分格式的构造:基于Taylor展开获得求解四阶问题的三层差分显格式和隐格式,它们的局部截断误差均为
。为了离散简支梁两端扰度为零这一边界条件而引入了人工边界条件,根据离散Fourier分析证明了当网比
时显格式稳定,而隐格式是绝对稳定的,数值实验证明了理论结果。
2. 差分格式的构造
2.1. 三层差分显格式的构造
取空间步长
和时间步长
,其中M是自然数。用两族平行直线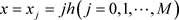
和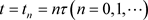 生成矩形网格,网格节点为
生成矩形网格,网格节点为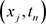 ,用
,用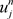 表示定义在网点
表示定义在网点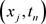 上的网函数。对(1.1)的第一个方程的左端在
上的网函数。对(1.1)的第一个方程的左端在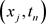 作Taylor展开有
作Taylor展开有
 。
。
略去高阶项得到连续方程的差分方程
 。
。
其截断误差的阶为 。令
。令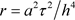 (网比),上述差分方程化为如下显格式
(网比),上述差分方程化为如下显格式
 。 (2.1)
。 (2.1)
2.2. 三层差分隐格式的构造
同样对(1.1)的第一个方程的左端在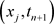 作Taylor展开有
作Taylor展开有
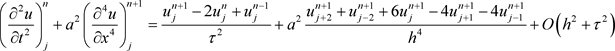 。
。
略去高阶项得到连续方程的差分方程
 。
。
其截断误差的阶为 。同样令
。同样令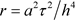 (网比),上述差分方程化为如下隐格式
(网比),上述差分方程化为如下隐格式
 。(2.2)
。(2.2)
由于(2.2)的系数矩阵严格对角占优,故(2.2)存在唯一解。在(2.1)和(2.2)中当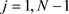 时,
时, 和
和 未知,为此,需引入人工边界。
未知,为此,需引入人工边界。
2.3. 人工边界
由边界条件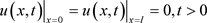 得
得
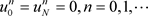 。 (2.3)
。 (2.3)
由于对边界条件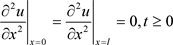 离散时,
离散时,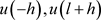 没有定义,因此需要引入人工边界条件:
没有定义,因此需要引入人工边界条件:
 。 (2.4)
。 (2.4)
注意(2.4)的截断误差为二阶。当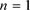 时,计算第二层除了已知第零层的值外还需要第一层的值。为
时,计算第二层除了已知第零层的值外还需要第一层的值。为
此,需利用初始速度来求第一层的值,但为保证截断误差的阶仍为二阶,可将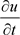 在
在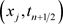 处展开,
处展开,
得到计算第一层的中心差商
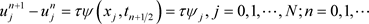 。 (2.5)
。 (2.5)
于是,(2.1),(2.3)~(2.5)给出了求解(1.1)显示差分方法。而(2.2),(2.3)~(2.5)给出了求解(1.1)的隐式差分方法。
3. 差分格式的稳定性分析
3.1. 显格式的稳定性
为了分析三层差分显格式的稳定性,需将其化为与之等价的二层差分方程组
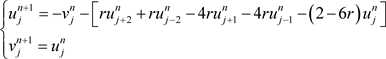 。
。
如果令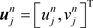 ,则上面的方程组可写成
,则上面的方程组可写成
 。
。
下面我们采用离散Fourier分析技术,设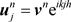 ,将其带入上式并消去公因子
,将其带入上式并消去公因子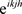 ,得到
,得到
 。
。
因此,增长矩阵为
 。
。
设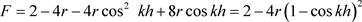 则
则 。其特征方程
。其特征方程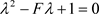 的解为
的解为
 。
。
当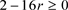 时,增长矩阵
时,增长矩阵 的谱半径
的谱半径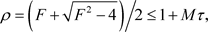 其中,M为正常数。所以要使得对所有的
其中,M为正常数。所以要使得对所有的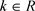 ,满足Von Neumann条件,即
,满足Von Neumann条件,即 ,当且仅当
,当且仅当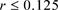 。
。
3.2. 隐格式的稳定性
将三层隐式差分格式(2.2)化成二层差分方程组
 。
。
令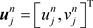 ,则上述方程组可写成:
,则上述方程组可写成:
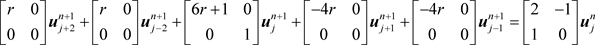 。
。
设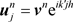 ,将其带入上述方程组并消去公因子
,将其带入上述方程组并消去公因子 ,得到
,得到
 。
。
令 ,上述方程组化为
,上述方程组化为
 。
。
因此,增长矩阵为
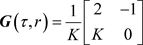 。
。
其特征方程的特征根为
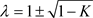 。
。
显然,对所有的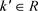 ,都有
,都有
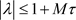 ,
,
其中M为常数,所以隐式格式是绝对稳定的。
4. 数值实验
在(1.1)中考虑
 ,
,
其解析解为
 。
。
图1的左图画的是在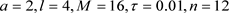 的数值位移逼近,此时
的数值位移逼近,此时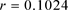 ;右图画的是在
;右图画的是在 的数值位移逼近,此时
的数值位移逼近,此时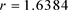 。表明显格式在
。表明显格式在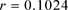 是稳定的,而在
是稳定的,而在 是不稳定的。
是不稳定的。
表1给出的是用隐格式计算的数值结果,当
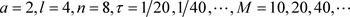
时数值误差的离散极大范 、离散
、离散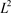 -范
-范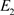 和实验收敛阶。可以看到:随着网格加密,即h和
和实验收敛阶。可以看到:随着网格加密,即h和 逐步减小,误差越来越小,并且关于时间和空间步长都达到了二阶精度。
逐步减小,误差越来越小,并且关于时间和空间步长都达到了二阶精度。

Table 1. Experiment convergence rate for the discrete maximum norm and -norm
表1. 离散极大范、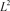 -范和实验收敛阶
-范和实验收敛阶
5. 结论
针对简支梁的横振动方程,基于Taylor展开,构造了求解四阶抛物方程的三层差分显格式和隐格式。它们的局部截断误差对时间和空间步长均为二阶精度。为了离散简支梁两端扰度为零这一边界条件而引入了人工边界条件,根据离散Fourier分析证明了显格式条件稳定,而隐格式绝对稳定。
基金项目
重庆市自然科学基金(CSTC, cstc2018jcyjAX0490),重庆市教委自然科学基金重点项目(KJZD-K201900701)。
NOTES
*通讯作者。