基于出租车运营数据的载客区域聚类及热点特征分析

Clustering Of Passenger Picked-Up Areas and Analysis of Hot Spots Based on Taxi Business Data

摘要: 为优化出租车空间资源调度，针对路网密集、数据密度差异较小条件下的城市出租车载客区域聚类问题，本文提出了一种采用OPTICS算法的聚类模型。通过实验与传统DBSCAN算法下的聚类结果进行对比，发现OPTICS算法更能有效地避免参数设置对实验结果的影响，解决传统DBSCAN算法在此类应用中聚类划分模糊的问题，达到出租车资源调度精细化的效果，对提升出租车载客率、降低空载时间具有现实指导作用。

Abstract: To optimize the taxi space resource dispatch, a clustering model using OPTICS algorithm is pro-posed for the clustering of taxi passenger carrying area under the condition of intensive road and small difference in data density. By comparing with the results of the traditional DBSCAN algorithm in experiment, it is found that the OPTICS algorithm can effectively eliminate the interference of parameter setting on the experimental results. It helps to the problem of traditional algorithm DBSCAN applied to such situation, and enhances the efficiency of taxi dispatch. This research has practical guiding effect on improving the load factor of taxi and reducing the time of idle load.

1. 引言

出租车市场供求不平衡问题是导致出租车司机收入、满意度下降的直接原因，间接导致司机调度距离过长，乘客超时等待取消订单等问题，直接制约出租车市场的发展，而出租车市场的供需不平衡问题往往具有短期、局部区域性等特点，如何更好地实现资源调度、满足出行需求是学术界和业界一直在探索的问题。

在互联网环境下，依托数据挖掘和大数据技术的发展，此类问题有着天然的应用场景和解决优势。郑林江等人 [1] 提出一种基于网格密度的聚类算法，将轨迹点投影在按网格划分的空间区域上，并根据轨迹点网格密度设定阈值，确认热点区域网格单元。Rami Ibrahim [2] 在研究中发现与随机交换聚类算法的聚类结果在均方误差和聚类质量上要优于基于层次密度的空间聚类算法。桂智明 [3] 基于MapReduce方法将出租车行驶轨迹中的轨迹点进行聚类并匹配路网得到其行驶轨迹，减少了轨迹中无意义簇的生成，实现了更具优势的轨迹聚类。姬波 [4] 基于信息论来研究出租车的空载密集区域，从而达到提高载客率的效果。毕硕本 [5] 使用Ripley’K函数检验出租车上下客事件的空间聚集关系，分析出租车运营的周期性变化特征及时空分布规律，发现出租车运营具有明显的早晚高峰期，且工作日和非工作日也有较大差别。曲昭伟 [6] 提出轨迹线密度方法，并实际运用于成都市春熙路商圈，根据当地路网密度值划分路段热点，识别热点位置，并依据实际的出行数据对该方法进行实证分析，发现该方法对出行需求量高的路段区域具有更明显的识别效果。Tang [7] 将DBSCAN应用于哈尔滨市不同区域的出租车上下客区域聚类，通过从DPS数据中提取的行程距离、时间、载客状态和非载客状态下的平均移动速度等影响因素来研究乘客的移动行为，并应用观测到的城市中心区OD矩阵建立了基于熵极大化方法的交通分布模型。

互联网条件下，出租车市场大量的运营数据有力地驱动本问题的解决。出租车需求在时间、空间上具有一定的相似性，而随着时间的推移，出租车需求在空间上不断地转移，形成一定潮汐效应的同时又有着实时差异。

为了探究城市出租车需求在时间上的精细变化，减少司机等待、空车时间，提升资源调度效率，本文将基于DBSCAN算法和OPTICS算法对出租车载客热点区域进行聚类划分并对比两种方法的聚类结果差异，证明OPTICS算法在应对簇间轮廓模糊的数据集时能更有效地划分簇结果，为具有不同路网类型的城市出租车载客热点预测提供新的参考。

2. 数据预处理

实验数据采自纽约市2009年~2015年间的100万条出租车运营数据，每一条数据包含一次出租车行程单的7个属性，包括乘客上车时间、上下车经纬度、乘客人数、费用等信息。

首先删除包含缺失值或明显异常值的数据；由于纽约城临海，行程起终点GPS定位信息落于海中的数据量要大于内陆城市，本文选择将起终点地点落于水域的数据删除，得到978,643条数据。

经过初步的数据清洗，噪音数据有效减少，即便仍存在的小部分起终点距离过大的数据难以区别是否真实有效，因其数据量不足一百条，不足以对实验产生明确影响。对时间数据进行变量分类转换，区分月份、星期几、第几小时等离散化变量。

新增行程起终点距离属性列，起终点距离为：

$\text{distance}=2R\cdot \text{arcsin}\sqrt{\text{haversin}(dR)}$

其中：

$\text{haversin}\left(\frac{d}{R}\right)=\text{haversin}\left({\phi }_2-{\phi }_1\right)+\cos \left({\phi }_1\right)\cdot \cos \left({\phi }_2\right)\cdot \text{haversin}(\Delta \lambda )$

$\text{haversin}\left(\theta \right)={\sin }^2(\theta 2)$

3. 聚类建模

3.1. DBSCAN算法介绍

DBSCAN算法 [8] 是最为知名的基于密度的聚类算法，尤其广泛应用于空间密度聚类领域。

概念：

假设具有样本集 $D=\left\{x_1,x_2,x_3,\cdots ,x_n\right\}$。

$\epsilon$ 邻域：对于任一点 $x_i\in D$，称为 $x_i$ 的邻域，邻域内所有的点与 $x_i$ 的距离都不大于 $\epsilon$， $x_i$ 在 $\epsilon$ 邻域内的点的集合为 $N_{\epsilon }\left(x_i\right)$。

$P_{\min }$ ：定义使得核心点成立的 $\epsilon$ 邻域内最低点数。

核心点：如果一个给定点 $x_i$ 在其 $\epsilon$ 邻域内至少有 个样本点，那么就称该给定点 $x_i$ 为核心点。

密度直达：对于核心点 $x_i$，如果存在样本点 $x_i$ 满足 $x_i$ 和 $x_j$ 间的距离不大于 $\epsilon$，那么称 $x_i$ 密度直达 $x_j$。

密度可达：对于一系列样本点 $x_t,x_{t+1},x_{t+2},\cdots ,x_{t+k}$，如果存在如下关系： $x_{t+m-1}$ 密度直达 $x_{t+m}$，那么密度可达 $x_{t+k}$。

密度相连：在给定 $\epsilon$ 及 $P_{\min }$ 条件下，存在样本点 $x_i,x_j$ 同时可由另一样本点 $x_k$ 密度可达，则称样本点 $x_i,x_j$ 密度相连。

DBSCAN算法核心思想可以解释为：对于样本集合中任意一个样本点 $x_i$，根据 $\epsilon$ 及 $P_{\min }$ 条件判断该样本点是否为核心点，若点 $x_i$ 是核心点，则依照密度直达的方式寻找其 $\epsilon$ 邻域内所有样本点集合

$N_{\epsilon }\left(x_i\right)=\left\{x_j|x_j\in D\wedge x_j\ne x_i\wedge \text{distance}\left(x_i,x_j\right)<\epsilon \right\}$，再判断 $N_{\epsilon }\left(x_i\right)$ 内所有点是否为核心点，重复该步骤

寻找所有由 $x_i$ 出发密度相连的点构成一个簇，直至样本集D中所有的点都落入某个簇集合或非簇集合。

DBSCAN作为一种基于空间密度地聚类算法，发现一个密度区域后以密度可达的方式拓展簇的范围，其聚簇轮廓往往是极不规则的，DBSCAN在面对非凸集数据的时候体现了出色的聚类能力及抗噪能力。

3.2. OPTICS算法介绍

OPTICS算法 [9] 是一种基于DBSCAN的改进算法。由于DBSCAN在面对未知数据分布情形下对 $\epsilon$ 邻域及P_min值过于敏感，不同的参数选择对于其聚类结果产生较大的影响，也容易影响其聚类质量，在面对不断变化的密度空间数据时缺乏可控性。针对以上缺点，学者对其提出了改进型算法OPTICS。

概念：

在DBSCAN相关概念的基础上，OPTICS算法引入了两个新的定义。

核心距离：样本 $x\in D$，对于给定 $\epsilon$ 和 $P_{\min }$，如果 $U\left(x,\epsilon \right)$ 内存在至少 $P_{\min }$ 个样本点，那么 $U\left(x,\epsilon \right)$ 内

与 距离相近的第 $P_{\min }$ 个点与x之间的距离就是x的核心距离。 $N_{\epsilon ,P_{\min }}\left(x\right)$ 为样本x在其 $\epsilon$ 邻域内距离x第

$P_{\min }$ 近的点，其数学表达式如下：

$\text{CoreDistance}\left(x\right)=\{\begin{array}{l}\text{undefined},\text{NumOf}\left(N_{\epsilon }\left(x\right)\right)<P_{\min }\\ \text{distance}\left(N_{\epsilon ,P_{\min }}\left(x\right),x\right),\text{else}\end{array}$

可达距离：样本 $x,y\in D$，对于给定 $\epsilon$ 和 $P_{\min }$， $x,y$ 之间的可达距离为：

$\text{ReachableDistance}\left(x\right)=\{\begin{array}{l}\text{undefined},\text{NumOf}\left(N_{\epsilon }\left(x\right)\right)<P_{\min }\\ \max \left(\text{CoreDistance}\left(x\right),\text{Distance}\left(x,y\right)\right),\text{else}\end{array}$

直接密度可达：对于样本 $x,y\in D$，若x为核心点， $\text{Distance}\left(x,y\right)<\epsilon$，则称x到y直接密度可达。

计算过程：

1) 输入数据样本集合 ，设置参数 $\epsilon$ 和 $P_{\min }$。

2) 初始化序列A和B。

3) 判断集合 中是否存在未处理样本点，是则转入步骤4，否则算法结束。

4) 选择一个 中未处理的核心点，将该核心点放入A序列，并将该核心点的直接密度可达点按可达距离升序排序放入B序列。

5) 判断B序列是否为空，是则转入步骤3，否则转入步骤6。

6) 选择B序列第一个点，将该点放入A序列，若该点为未处理核心点则将该点直接密度可达点放入B序列，并将B序列重新排序，否则转入步骤5。

7) 重复步骤3。

8) 算法结束。

4. 评价标准

Davies-Boulding指数(DBI)

DBI指数戴维森堡丁指数 [10]，是一种针对聚类结果的无监督评价指标，由Davies, D.L.，Bouldin, D.W.提出。该方法首先定义了一个变量 $S_i$ ：

$S_i={\left(\frac{1}{T_i}\underset{j=1}{\overset{T_i}{{\displaystyle \sum }}}{\left|X_j-A_i\right|}^p\right)}^{\frac{1}{p}}$

式中 $T_i$ 代表第i个簇中的数据点个数， $X_j$ 代表簇i中的第j个数据点， $A_i$ 为簇i的簇核心，p值用于调整距离计算方法；变量 $S_i$ 衡量的是簇内样本点与簇核心的距离均值。

其次，DBI指数定义了变量 $M_{i,j}$ ：

$M_{i,j}={\left(\underset{k=1}{\overset{n}{{\displaystyle \sum }}}{\left|a_{k,i}-a_{k,j}\right|}^p\right)}^{\frac{1}{p}}$

$a_{k,i}$ 表示第i个簇的簇核心的第k个属性值，也就是说， $M_{i,j}$ 衡量的是第i个簇和第j个簇的簇核心间距。

随后，DBI指数定义了变量 $R_{i,j}$ ：

$R_{i,j}=\frac{s_i+s_j}{M_{i,j}}$

$R_{i,j}$ 用于衡量第i个簇和第j个簇之间的相似度。

$R_i$ 则为第i个簇与其他簇的相似度的最大值：

$R_i=\max \left(R_{i,j}\right)$

最终得到DBI指数：

$\text{DBI}=\frac{1}{n}\underset{i=1}{\overset{N}{{\displaystyle \sum }}}{R}_i$

可见，DBI指数非常良好地解释了聚类结果的离散程度，当同一簇内样本点离散程度较低而样本集合内各个簇核心间距较大时，DBI指数较小，聚类结果簇集划分效果较明显。

5. 实验

实验环境：Windows10 x86操作系统，Python为3.6版本，scikit-learn为0.21.3版本。

对本数据集打车起终点距离进行统计，统计结果如图1所示。

Figure 1. Distance frequency chart of the taxi journey

图1. 打车起终点距离频数分布

数据表明，本数据集打车起终点距离均值为3.32千米，标准差为3.73千米，50%的行程起终点距离在1.25千米至3.92千米之间，图1横轴位于10千米和20千米处各有一个较为明显的突起，通过后续聚类结果发现原因为该城市航空公共交通基础设施客流聚集。可以看出，打车需求以中短程需求为主。

考虑到随时间推移城市交通设施结构的变化对数据的影响，本文选择2013、2014年周一至周五9:00~10:00期间产生的行程数据作为模型输入。

5.1. DBSCAN算法实验

使用DBSCAN对其空间位置进行聚类，通过网格搜索的方式确定一个较为合理的聚类结果，选择在 $\epsilon$ 邻域取值100米， $P_{\min }$ 取值14条件下，其空间聚类结果如图2所示，灰色点为非簇样本，粉色点为所有样本数低于100的簇样本。

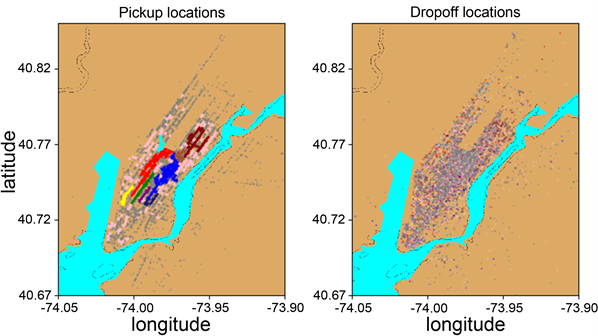
Figure 2. Result of DBSCAN clustering experiment

图2. DBSCAN算法空间聚类结果

5.2. OPTICS算法实验

使用OPTICS对同一数据进行聚类，同样使用网格搜索的方式寻找局部较优参数，设置 $P_{\min }$ 为5，max_eps为0.05千米，空间聚类结果如图3所示，灰色点为非簇样本，共有9个样本数大于100的彩色簇集。

Figure 3. Result of OPTICS clustering experiment

图3. DBSCAN算法空间聚类结果

5.3. 实验结果统计与分析

两种方法得出的主要簇样本统计结果如表1~2所示。

Table 1. Statistics of the main clusters under DBSCAN

表1. DBSCAN聚类结果主要簇的样本点统计

Table 2. Statistics of the main clusters under OPTICS

表2. OPTICS聚类结果主要簇的样本点统计

Table 3. Comparison of clustering results under DBSCAN and OPTICS

表3. DBSCAN和OPTICS算法下聚类结果对比

根据实验结果的统计数据可知，OPTICS算法下的实验结果具有更低的DBI指数，这表明各簇内样本点的离散程度低而簇间核心间距较大，具有明显的聚簇划分效果。本方法相较于常用的DBSCAN方法更利于出租车载客区域空间密度的划分，便于运营人员明确核心区域中心，将空载率高的区域车辆向高载客频率区域调度，减少出租车空载时间和乘客等待时间。

6. 结论

由于纽约市出租车载客区域更为密集，且簇间轮廓较为模糊，特定城市的载客热点聚类应当因地制宜采用不同的方法，本文在前人研究的基础上，分别采用DBSCAN和OPTICS两种算法对纽约市出租车载客区域进行了聚类划分，多次调参取得实验结果差异如表3所示，DBI差异明显，可见OPTICS算法在面对簇间轮廓模糊的数据集时可以很大程度上避免 $\epsilon$ 邻域及 $P_{\min }$ 值设置所带来的实验干扰，聚类效果强于DBSCAN。

本研究有助于解决不同城市路网条件下出租车的资源调度问题，对大数据精细化运营有重要的现实意义。