微动特征提取递归分解快速傅里叶变换算法的研究及应用

Research and Application on a Recursively Fast Fourier Transformation Decomposion Algorithm for Micro-Motion Features Extraction

摘要: 针对雷达目标微动特征提取提出一种递归分解快速傅里叶变换算法，并使用C语言编程实现。算法可对任意非素数点数序列实现快速离散傅里叶变换。以复数乘法和加法次数为指标对算法进行性能分析，结果表明对序列点数为2的整次幂，算法效率与传统基–2快速傅里叶变换算法相同；对其它序列点数为非素数情况，算法效率优于直接计算离散傅里叶变换且简化了对输入序列重排过程。目前该算法已应用于雷达信号处理的微动目标特征提取中。

Abstract: Aiming at micro-motion features extraction on radar targets, a recursively fast Fourier transfor-mation (FFT) decomposition algorithm is proposed, which is programmed and implemented in the C language. In this algorithm the fast discrete Fourier transformation is carried out on an arbitrary selected sequence whose elements are at a non-prime number. Performance analysis is addressed on the specification of complex multiplication and addition rounds. It demonstrates that if the number of sequence elements equals 2 raised to an integer power, the algorithm efficiency is the same as the traditional 2-based FFT algorithm, whereas if the number doesn’t but it is still a non-prime number, this efficiency is superior to the direct discrete Fourier transformation com-puting. Furthermore, this algorithm simplifies the process of rearranging the input sequences. Currently this algorithm is utilized in the micro-motion target features extraction in radar signal processings.

1. 绪论

一般将目标或目标部件除质心平动以外的振动、转动和锥旋等微小运动称为微动。微动在自然界普遍存在，如人行走时四肢的摆动、桥梁的振动、天线的转动、电动机的转动、直升机旋翼的转动和弹头的进动等。微动通常由目标的质量分布特性和动力学特性等物理属性决定，是目标固有的运动形式。微动的存在为提取与目标物理属性相关的特征量提供了可能，为雷达非合作目标探测和识别提供了新的途径。雷达目标微动特征刻画了目标的运动状态和特点，是近年来雷达目标探测与识别的热点研究领域 [1]。离散傅里叶变换(Discrete Fourier Transform, DFT)在雷达目标微动特征提取中起着非常重要的作用，其原因之一是计算DFT有著名的快速傅里叶变换(Fast Fourier Transform, FFT)算法。概括来讲，作为DFT的一种快速算法，FFT在雷达信号处理、语音信号处理、图像处理、功率谱估计、系统的分析、仿真等各个领域都得到了极为广泛的应用。在FFT的具体计算上，传统做法是采用时域抽取或频域抽取的基-2算法，这种算法执行效率较高，应用方便，但要求序列点数N是2的整数次幂( $N=2^M$ )，这里M为整数。如果N不是2的整数次幂，根据DFT的性质，有限长序列补“0”后不影响其频谱，只是使频谱采样点数增加，可对序列样本补充适当数量的零值，使得( $N=2^M$ )，然后采用基-2算法计算DFT。对雷达目标微动特征提取来说，这种方法有时要补上太多的零点，很不经济，且FFT的计算时间也较长。例如某雷达目标微动特征提取过程中需要处理的序列点数N = 2988，要使N增加到邻近的且等于2之整数幂的数，必增加4096 – 2988 = 1108个零值，显然计算量对时间响应要求较高的探测与识别目标而言增加得太多了 [2]。针对这种情况，有文献提出了素因子分解算法，但这种算法需要对输入序列进行复杂的变换，在实际中应用不多 [1] - [11]。

本文以素因子算法为基础，针对雷达目标微动特征提取需要，研究序列点数N为任意非素数时的FFT算法，避免对序列进行复杂的变换。下面按照这一思路分两步进行研究：首先研究任意因子单次分解FFT算法，在此基础上进一步利用递归方法得到最终FFT结果，用C语言实现FFT，最后以复数乘法和加法次数评估递归分解FFT算法的性能。需要说明的是，基于离散傅里叶变换对的性质 [2]，本文提出的递归分解FFT算法显然适用于离散傅里叶逆变换(Inverse Fast Fourier Transform, IFFT)算法。

2. 任意因子单次分解FFT算法

这里的“任意”指对N的因子没有特殊要求，即一般情形。为叙述方便，不妨设序列点数N = MB，这里M、B均为任意整数。考虑时域离散序列

$x\left[n\right],n=0,1,\cdots ,N-1$ (1)

其中n为时间变量。为计算x[n]的DFT，引入 $W_N={\text{e}}^{-j\frac{2\pi }{N}}$，则对频域 $k=0,1,\cdots ,N-1$ 有

$\begin{array}{c}X\left[k\right]=\text{DFT}\left\{x\left[n\right]\right\}={\displaystyle \underset{n=0}{\overset{N-1}{\sum }}x\left[n\right]W_N^{kn}}\\ ={\displaystyle \underset{n=0}{\overset{M-1}{\sum }}x\left[Bn\right]W_N^{kBn}}+{\displaystyle \underset{n=0}{\overset{M-1}{\sum }}x\left[Bn+1\right]W_N^{k\left(Bn+1\right)}}+{\displaystyle \underset{n=0}{\overset{M-1}{\sum }}x\left[Bn+2\right]W_N^{k\left(Bn+2\right)}}+\cdots +{\displaystyle \underset{n=0}{\overset{M-1}{\sum }}x\left[Bn+B-1\right]W_N^{k\left(Bn+B-1\right)}}\\ \text{=}{\displaystyle \underset{n=0}{\overset{M-1}{\sum }}x\left[Bn\right]W_{MB}^{kBn}}+{\displaystyle \underset{n=0}{\overset{M-1}{\sum }}x\left[Bn+1\right]W_{MB}^{k\left(Bn+1\right)}}+{\displaystyle \underset{n=0}{\overset{M-1}{\sum }}x\left[Bn+2\right]W_{MB}^{k\left(Bn+2\right)}}+\cdots +{\displaystyle \underset{n=0}{\overset{M-1}{\sum }}x\left[Bn+B-1\right]W_{MB}^{k\left(Bn+B-1\right)}}\\ \text{=}{\displaystyle \underset{n=0}{\overset{M-1}{\sum }}x\left[Bn\right]W_M^{kn}}+W_N^k{\displaystyle \underset{n=0}{\overset{M-1}{\sum }}x\left[Bn+1\right]W_M^{kn}}+W_N^{2k}{\displaystyle \underset{n=0}{\overset{M-1}{\sum }}x\left[Bn+2\right]W_M^{kn}}+\cdots +W_N^{\left(B-1\right)k}{\displaystyle \underset{n=0}{\overset{M-1}{\sum }}x\left[Bn+B-1\right]W_M^{kn}}\end{array}$ (2)

可以看出，如果令

$X_b\left[k\right]={\displaystyle \underset{n=0}{\overset{M-1}{\sum }}x\left[Bn+b\right]W_M^{kn}},b=0,1,\cdots ,B-1;k=0,1,\cdots ,M-1$ (3)

则 $X_b\left[k\right]$ 是 $x\left[Bn+b\right]$ 的M点DFT，即 $X_b\left[k\right]=\text{DFT}\left\{x\left[Bn+b\right]\right\}$，利用离散傅里叶级数的周期性，式(2)可表示为

$X\left[k\right]={\displaystyle \underset{b=0}{\overset{B-1}{\sum }}{W}_N^{bk}{X}_b\left[k\mathrm{mod}M\right]},k=0,1,\cdots ,N-1$ (4)

其中k mod M表示k以M为模取余。

众所周知，对复数乘法和加法而言，直接计算DFT时的运算量大致与N²成正比，现式(4)把一个N点DFT分解为B个M点DFT，降低了运算量。为进一步用X_b[k]表示X[k]，作下列变量替换

$k=k^{\prime }+b^{\prime }M,k^{\prime }=0,1,\cdots ,M-1;b^{\prime }=0,1,\cdots ,B-1$ (5)

可得

$\begin{array}{c}X\left[k\right]=X\left[k^{\prime }+b^{\prime }M\right]\\ =X_0\left[k^{\prime }\right]+W_N^{k^{\prime }}{W}_B^{b^{\prime }}{X}_1\left[k^{\prime }\right]+W_N^{2k^{\prime }}{W}_B^{2b^{\prime }}{X}_2\left[k^{\prime }\right]+\cdots +W_N^{\left(B-1\right)k^{\prime }}{W}_B^{\left(B-1\right)b^{\prime }}{X}_{B-1}\left[k^{\prime }\right]\\ ={\displaystyle \underset{b=0}{\overset{B-1}{\sum }}\left\{W_N^{b{k}^{\prime }}{W}_B^{b{b}^{\prime }}{X}_b\left[k^{\prime }\right]\right\}}\end{array}$ (6)

根据式(6)得到任意因子单次分解FFT算法流图，如图1所示，图中B取2，这时 $W_2^1=-1$。从图1可以看出，B因子单次分解FFT算法共包含M个蝶形运算单元。

3. 递归分解FFT算法

在数学和计算机科学中，递归是指一个函数直接或间接调用自身的现象。作为一种算法，递归在程序设计语言中得到了广泛的应用，它通常把一个大型复杂的问题层层转化为一个与原问题相似但规模较小的问题来求解。使用递归，只需少量程序代码就可以描述解决问题所需的多次重复操作，因此大大减少了代码量，提高了程序设计效率。在上述任意因子单次分解FFT算法基础上，不难得到递归分解FFT算法，如图2所示。

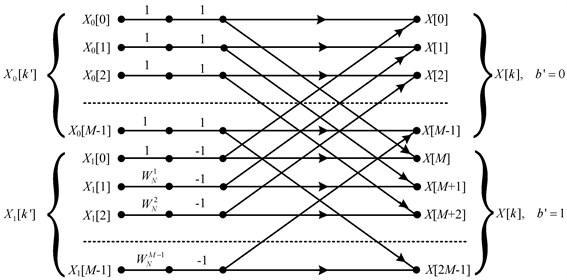
Figure 1. A flowchart of one single arbitrary factor FFT decomposition algorithm where B = 2

图1. 任意因子单次分解FFT算法流图，B = 2

图2中，流程开始对DFT点数N是否为素数进行判断：若N为素数，FFT算法将失效，此时只能直接计算DFT。对N为非素数的情况，当N为2的整次幂时，为提高效率采用传统基-2 FFT算法执行DFT。当N为其它非素数时，将N进行分解，并使分解后各因子按从大到小的顺序排列，进入递归处理过程：对N的每个因子，都按照式(2)构建 $x\left[Bn+b\right]$，利用上述单次分解FFT算法计算其DFT，得到 $X_b\left[k\right]=\text{DFT}\left\{x\left[Bn+b\right]\right\}$，最后利用式(6)得到X[k]。因此这里“递归”的含义体现在对N的每个因子计算DFT的过程中。容易看出，在构建 $x\left[Bn+b\right]$ 的过程中流程执行的是赋值操作，而不是像基-2FFT算法中那样对序列进行变址运算，也不像素因子算法那样对序列进行复杂的变址运算，因此简化了输入序列重排过程，也提高了处理速度。

考虑到篇幅，这里只给出递归分解FFT算法实现中的部分C函数代码：

void RDFFT(int N, double *xr, double *xi, double *XR, double *XI,

double *COS, double *SIN, const int& N0, int C)

{

……

double **ppR = new double *[B];

double **ppI = new double *[B];

for (int b = 0; b < B; ++b) {

ppR[b] = new double[N1];

ppI[b] = new double[N1];

for (int i = 0; i < N1; ++i) {

ppR[b][i] = xr[i * B + b];

ppI[b][i] = xi[i * B + b];

}

}

// recursively working

for (int b = 0; b < B; ++b)

RDFFT(N1, ppR[b], ppI[b], xr + b * N1, xi + b * N1, COS, SIN, N0, C * B);

……

}

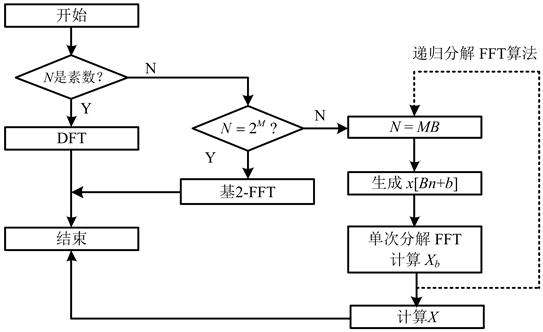
Figure 2. A flowchart of the recursively FFT decomposition algorithm

图2. 递归分解FFT算法流程图

4. 性能评估

现在基于递归分解FFT算法中所需乘法和加法运算次数对算法性能作出评估，因为当算法应用在通用计算机或专用处理器上时，乘法和加法的次数直接决定着计算速度。令 $\mu \left(N\right)$ 、 $\lambda \left(N\right)$ 分别表示递归分解FFT算法完成N点DFT所需的乘法和加法次数，根据式(6)不难得到

$\begin{array}{l}\mu \left(BM\right)=\{\begin{array}{l}B\mu \left(M\right)+\left(B-1\right)\left(M-1\right),B=2\\ B\mu \left(M\right)+\left(B-1\right)M,B\ne 2\end{array}\\ \lambda \left(BM\right)=B\lambda \left(M\right)+\left(B-1\right)BM\end{array}$ (7)

在此基础上定义

$\alpha \left(N\right)=\frac{\mu \left(N\right)}{N^2},\beta \left(N\right)=\frac{\lambda \left(N\right)}{N\left(N-1\right)}$ (8)

显然 $\alpha \left(N\right)$ 、 $\beta \left(N\right)$ 分别为采用递归分解FFT与直接计算DFT这两种情况下复数乘法和加法次数的比， $\alpha \left(N\right)$ 、 $\beta \left(N\right)$ 越大于1，表明递归分解FFT算法的性能越好。图3为根据式(8)得到的 $\alpha =\alpha \left(N\right)$ 、 $\beta =\beta \left(N\right)$ 随N的变化情况，其中N为2到3000间的所有非素数。从图3可以看出几乎在所有N的情况下 $\alpha$ 、 $\beta$ 远远大于1，表明递归分解FFT算法性能远远超过直接计算DFT，且随着N的增大，这种优异性越来越明显。

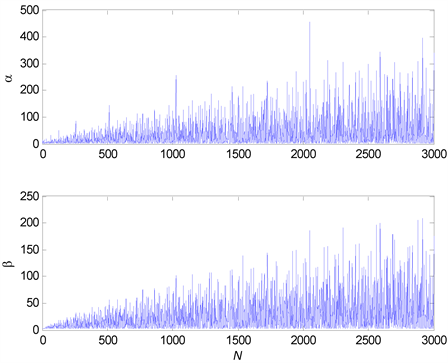
Figure 3. Performance evaluation of the recursively FFT decomposition algorithm

图3. 递归分解FFT算法性能评估

图4是使用本文提出的递归分解FFT算法对某雷达目标提取微动特征时的运行界面，从图中不难计算出进动周期大约为2.3秒。

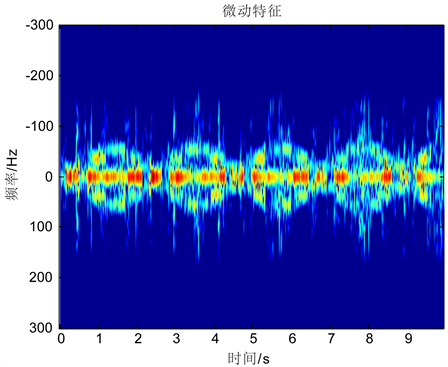
Figure 4. Radar target micro-motion features extraction based on an recursively FFT decomposition algorithm

图4. 使用递归分解FFT算法提取雷达目标微动特征

5. 结束语

为提高雷达目标微动特征提取处理速度，本文提出了一种递归分解FFT算法。算法适用范围广，即只要求N为非素数。进一步如果N是2的整数次幂，算法采用基-2 FFT算法，否则以单次分解为基础进行递归处理得到频域序列。在工程实践中的应用结果表明，本算法提高了雷达目标探测与识别中数据处理效率。