1. 引言
混沌时间序列预测在气象预测 [1] 、水利预测 [2] 、通信 [3] 等方面应用广泛。近年来,国内外学者提出了许多混沌预测模型,如:混沌线性回归模型、神经网络、支持向量机和局部多项式模型等。易锦燕 [4] (2015)将混沌时间序列线性回归模型应用于供应链的绩效预测。贺坤 [5] (2018)提出了一种基于集合经验模态分解(EEMD)和遗传算法(GA)优化的神经网络(BP)的预测模型。崔万照 [6] (2004)建立了混沌时间序列的支持向量机预测模型。周永道 [7] (2007)把混沌时间序列构造为一组序列对,然后用多元局部多项式方法来预测其序列。这些学者的研究都有一定的参考性,但单个预测模型都有自身的特点和应用局限性,所以反应数据信息存在一定差异,使用单个模型进行预测都难免丢失部分数据信息。
由于单个预测模型自身的缺点及局限性,采用单个预测模型相结合的组合预测模型 [8] [9] [10],越来越成为研究发展的需要。在组合预测方面,谢朋朋 [11] (2015)研究基于线性回归预测模型和灰色模型GM (1,1)的变权组合预测模型。俞凯加 [12] (2015)利用ARIMA时间序列模型和BP神经网络模型的组合预测模型获得大坝变形的预测。刘伟军 [13] (2015)提出混沌SVM与BP神经网络组合预测模型用于工程造价指数预测。本文结合混沌线性回归模型和Elman神经网络模型,通过加权算术平均算子进行组合,构建一种新型预测模型,用于Lorenz混沌时间序列 [14] 预测研究。本文的组合预测模型,不仅有线性模型,还有非线性模型,将线性模型和非线性模型进行组合,使得该组合预测模型能够有效的预测混沌时间序列,预测精度高,且预测精度明显优于单个混沌线性回归模型和Elman神经网络模型。
2. 理论模型设计
2.1. 混沌线性回归模型
建立混沌线性回归模型的步骤如下:第一步对混沌时间序列进行相空间重构 [15],第二步根据重构的相空间建立线性回归模型。
2.1.1. 相空间重构
对于混沌时间序列
,其在重构相空间中的某一相点可以表示为:
,其中,
,
。Takens定理指出,对于重构后的相空间轨迹中的每一点,存在光滑映射
,使得:
,其中
。若能求出f或者找到f的近似映射
,便可对下一个数据点
进行预测。本文采用互信息函数法 [16] 求解延迟时间
,采用Cao [17] 的方法求解嵌入维数m。
2.1.2. 线性回归模型
重构相空间之后建立混沌时间序列
的线性回归模型来近似映射f:
(1)
(2)
其中:
,
,
,
。
由最小二乘理论推导出:
(3)
利用混沌时间序列的混沌特性,对混沌时间序列相空间重构,再结合线性回归模型建立混沌线性回归模型。该模型对混沌时间序列具有较高的预测精度。
2.2. Elman神经网络模型
Elman神经网络是一种典型的动态递归神经网络,它是在BP网络结构基础上,在隐含层增加一个承接层,作为一步延时算子,从而使系统具有适应时变性的能力。因此,考虑混沌时间序列的动态特点,尝试使用Elman神经网络对混沌时间序列进行预测。
2.2.1. Elman神经网络结构
Elman神经网络分为四层:输入层、隐藏层、承接层和输出层,如图1所示。输入层、隐藏层、输出层的连接类似前馈网络,其连接权可以学习修正。承接层从隐藏层接收反馈信息,每一个隐藏层节点都要一个与之对应的承接层节点连接。承接层的作用是通过连接记忆将上一个时刻的隐藏层的输出,连同当前时刻的网络输入一起作为隐藏层的输入。这种反馈方式使网络对历史状态的数据具有敏感性,增加了网络本身处理动态信息的能力,从而达到动态建模的目的 [18] [19]。这种反馈方式可以很好的体现混沌时间序列的动态过程。

Figure 1. Elman neural network structure diagram
图1. Elman神经网络结构图
2.2.2. Elman神经网络学习过程
Elman神经网络的输入矢量为Y(t),输出矢量为
,隐藏层输出矢量为X(t),承接层输出矢量为Xc(t),则Elman神经网络输入输出关系为:
(4)
(5)
(6)
其中w1,w2,w3,分别表示承接层到隐藏层、输入层到隐藏层、隐藏层到输出层的连接权值;
和
分别为隐藏层和输出层神经元的传递函数。Elman神经网络采用BP算法进行权值修正,学习损失函数采用误差平方和函数:
(7)
其中
为混沌时间序列的预测值。Elman神经网络模型体现了混沌时间序列的动态过程,因此该模型对混沌时间序列具有较高的预测精度。
2.3. 组合预测模型
组合预测模型的普遍形式为单个预测模型的加权平均,因此组合预测模型的重点在于加权系数的确定。对于混沌时间序列预测问题,采集到的历史数据为
向量。采用混沌线性回归模型和Elman神
经网络模型进行预测,得到2个预测模型
,其在t时刻的预测值分别为
。设权重向量
为组合预测模型的组合加权权重,且满足
。本文的组合预测模型为:
(8)
用均方误差作为目标函数 [20] [21],能够有效避免正负抵消的情况,求出的权重能够提高组合模型的预测效果。权重向量的分量取值范围为0到1,且分量求和等于1,所以本文可假设
,
。根据实际情况,可考虑
为0到1步长为0.1之间的数。然后遍历
,选取使得目标函数达到最小的数作为最终的
。该组合预测模型同时包含了线性模型和非线性模型的特点,因此该模型对混沌时间序列具有很好的预测精度。
3. 仿真实验结果及分析
3.1. Lorenz系统下实验条件说明
本文主要验证组合预测模型在预测精度方面的性能,进行三个仿真实验。以Lorenz系统生成的序列作为实验的混沌时间序列。预测精度采用均方误差(MSE)、平均绝对误差(MAD)和均方根误差(RMSE) 3个指标 [22] [23] 来衡量。均方误差衡量真实值与预测值的差异程度,平均绝对误差是所有单个观测值与预测值的偏差的绝对值的平均,均方根误差是均方误差的算术平方根。
为真实值,
为组合预测模型的预测值,n表示数量。3个指标计算公式如下:
(9)
(10)
(11)
Lorenz系统生成混沌时间序列,Lorenz系统迭代方程如下:
(12)
其中
为时间函数,该系统在Lorenz先生给出的典型参数下的显式(Runge-Kutta)数值解具有混沌效应,典型参数
。假定初始条件
,采样时间
秒,产生10,000个数据点,取其中的第一分量
作为混沌时间序列
,选取4000个连续序列作为采样数据。采用复自相关法和Cao的方法确定出
的延迟时间
,嵌入维数
。
3.2. 混沌线性回归模型效果评估
采用Lorenz系统生成混沌时间序列作为历史数据。为了在预测精度上对比验证本文提出的组合预测模型性能,用混沌线性回归模型和Elman神经网络模型的预测结果作对比。
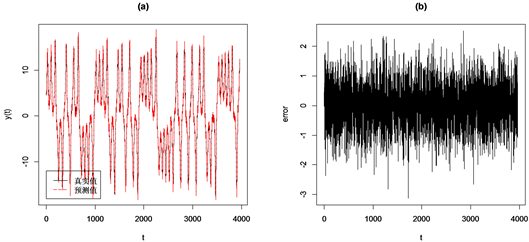
Figure 2. Chaotic linear regression model prediction results. (a) Prediction curve; (b) Error curve
图2. 混沌线性回归模型预测结果。(a) 预测曲线;(b) 误差曲线
图2(a)代表3964个观测数据在混沌线性回归模型下的预测曲线,从图中可以看出,红色虚线的预测曲线很好的拟合了黑色的实际曲线,均方误差MSE为0.5680。图2(b)观测数据的预测误差曲线,从图中可以看出,各点的预测误差集中在零点附近波动,说明混沌线性回归模型的预测误差较小。
3.3. Elman神经网络模型效果评估
Elman神经网络采用的是BP算法 [24] [25] 进去权值修正,所以需要先对混沌时间序列归一化处理,然后对预测的数据反归一化作为最终的预测值。本来Elman网络的输入层数为6,隐藏层数为3,承接层数为3,输出层数为1。
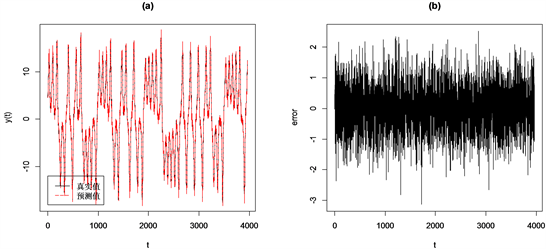
Figure 3. Elman neural network model prediction results. (a) Prediction curve; (b) Error curve
图3. Elman神经网络模型预测结果。(a) 预测曲线;(b) 误差曲线
图3(a)代表3964个观测数据在Elman神经网络模型下的预测曲线,从图中可以看出,红色虚线的预测曲线很好的拟合了黑色的实际曲线,均方误差MSE为0.7731。图3(b)观测数据的预测误差曲线,从图中可以看出,各点的预测误差集中在零点附近波动,说明Elman神经网络模型的预测误差较小。
3.4. 组合预测模型效果评估
对比混沌线性回归模型和Elman神经网络模型的预测结果可知,两种方法对混沌时间序列的预测存在一定差异。为了有效整合这两种预测方法的优点,将两种方法通过加权算术平均算子进行组合,得到新的组合预测模型。计算得到混沌线性回归模型和Elman神经网络模型的权值为0.53和0.47。
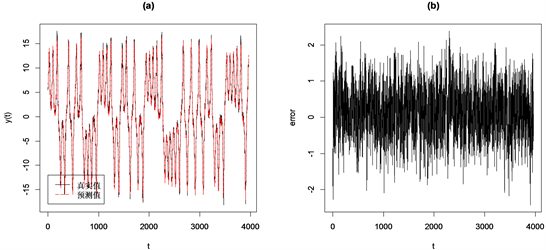
Figure 4. Combined prediction model prediction results. (a) Prediction curve; (b) Error curve
图4. 组合预测模型预测结果。(a) 预测曲线;(b) 误差曲线
图4(a)代表3964个观测数据在组合预测模型下的预测曲线,从图中可以看出,红色虚线的预测曲线很好的拟合了黑色的实际曲线,均方误差MSE为0.4644。图4(b)观测数据的预测误差曲线,从图中可以看出,各点的预测误差集中在零点附近波动,说明组合预测模型的预测误差较小。
3.5. 单个模型与组合预测模型效果对比
为了在预测精度和稳定性上对比验证组合预测模型的性能,在相同的实验条件下,分别采用混沌线性回归模型、Elman神经网络模型和组合预测模型对Lorenz时间序列进行单步预测,统计得到均方误差MSE,平均绝对误差MAD,均方根误差RMSE。表1给出了不同模型对Lorenz混沌时间序列的预测结果。

Table 1. Comparison of different prediction models
表1. 不同预测模型比较
从表1可以看出,组合预测模型的MSE、MAD、RMSE均明显小于单个模型,在预测精度和稳定性方面,组合预测模型具有明显的优势。虽然组合预测模型运行的时间相比于单个模型长,但都来可接受范围。总体看来,在混沌时间序列预测中,组合预测模型在预测精度和稳定性上更具有优势。
4. 结论
单个预测模型由于自身条件的限制,对混沌时间序列进行预测时,由于不能完全利用数据信息而影响预测效果。通过一定方式对单个模型进行组合,得到新的组合预测模型能够提高预测精度。本文设计了一种由混沌线性回归模型和Elman神经网络模型相结合的组合预测模型,并通过Lorenz混沌时间序列验证了这种预测方法的有效性。这种组合预测模型在预测精度和稳定性上优于这两个单个模型,以MSE、MAD、RMSE这3个指标说明了,本文提出的组合预测模型在Lorenz混沌时间序列的有效性。因此可将本文方法推广运用到混沌保密通信、海杂波处理、生物医学等领域。
基金项目
重庆市自然科学基金(cstc2018jcyjAX0464),重庆市研究生教育教学改革研究重大项目(yjg191017),重庆市高等教育教学改革研究一般项目(193180),重庆理工大学高等教育教学改革研究重点项目(2018ZD05),重庆理工大学研究生教育教学改革研究重点项目(2017yjg102),重庆市专业学位研究生教学案例库建设项目(201967,应用统计专业学位研究生教学案例建设)。
NOTES
*通讯作者。