关于概率空间的思辨教学

Speculative Teaching on Probability Space

摘要: 概率空间是概率论中的重要概念，是所有知识和问题的依赖平台，本文通过思辨教学的形式解释了概率空间的来源，并利用概率空间的不同建立方式来解决问题，有利于培养学生多维度思维能力。

Abstract: Probability space is an important concept in probability theory and a platform for all knowledge and problems. This paper explains the origin of probability space through speculative teaching, and uses different ways of building probability space to solve problems, which is conducive to cultivating students’ multi-dimensional thinking ability.

1. 引言

概率统计发展到今天，内容十分丰富，应用广泛，因此在各大学中，概率统计成为理工科专业必修的一门课程。概率统计是所有大学数学课程中与应用联系最为紧密的，其思想方法与之前大部分描述确定性理论的课程不同，它独特的处理随机的思想使得学生接受起来会产生理解上的误解，又因严格理论基础需要测度论，使得许多概念难以解释清楚。但作为大学课程，仅仅如高中那样进行算法教学，告诉其定理公式，依照套路，方法做题，通过考试是不够的。大学课堂上更应注重思辨教学方式，思辨数学就是动态地辩证地把握概念和体味推据，凭借对概念的直觉和数学美的启迪(而非逻辑性的推理)，产生直观的解题思路方法或做出合情推理决策 [1]。据这种思考方式，来挖掘问题的来源，探索解决问题的数学思维方法，延伸概念的内涵外延，有助于更好培养学生的独立思考和质疑的能力。

概率空间是概率论中的重要概念，是所有知识和问题的依赖平台，但在初等概率论中很难将这一概念严格地化，过于严格化又造成理解上的困难。很多课堂上只能告诉学生一个抽象的定义，让其记住性质，却不能深刻理解为什么这样定义，来源哪里。本文总结了历年教学经验，尝试进行思辨方法，对概率空间的教学进行追根求源和实例详解的分析，期望学生更好地理解应用基本概念。

2. 概率空间概念教学的追根求源

在目前大部分概率统计教材 [2] 中大致都是如下介绍概率空间。先考察特殊的概率模型：古典概率模型，频率，几何概率模型，总结出三条共有的特征给出以下定义：

设 $E$ 是随机试验， $S$ 是它的样本空间， $\sigma$ 是某些子集的集合，对于 $\sigma$ 的每一个事件 $A$ 赋予一个实数，记为 $P\left(A\right)$，若 $P\left(A\right)$ 满足下列三个条件：1) 非负性：对每一个事件 $A$，有 $P\left(A\right)\ge 0$；2) 完备性： $P\left(S\right)=1$；3) 可列可加性：设 $A_1,A_2,\cdots$ 是两两互不相容的事件，则有 $P\left({\displaystyle {\cup }_{i=1}^{\infty }{A}_i}\right)={\displaystyle \underset{i=1}{\overset{\infty }{\sum }}P\left(A_i\right)}$。则称 $P\left(A\right)$ 为事件 $A$ 的概率，( $S$, $\sigma$, P)为一概率空间。这样的讲述有两个问题被回避了：概率作为从集合到数的映射具有很多性质，为什么在定义中只考察这三种性质，特别是可列可加性？为什么概率定义在S的部分子集上？而不是全部子集上？虽然严格的解释需要测度论，但仍然可以给学生一个引导，来分析是如何思考和解决新问题的。在这里可以尝试做了如下解释：集合到数的映射给出了对集合的一种度量，比如区间的长度，平面区域的面积，空间区域的体积，都可以看作是对集合的一种度量，这个度量可以在纵横两方面推广，直线上比区间更复杂的点集是否可有“长度”的概念？n维空间的点集的度量是什么？这就引入测度的概念，用来度量一个集合E的“大小”，记为m(E)，作为长度，面积，体积的一种推广方式，自然要求满足一定的条件才合理，比如m作用在区间上仍然是长度，具有长度已有的性质：有限可加性，可列可加性。但这些限制无法使得一切点集合都有度量，从而对点集的结构有一定要求，在一类特殊的子集上可以定义满足条件的测度。而这个概率就是一种归一化的测度。这样的解释虽然不够严格，却给出了直观的思维方式，理解程度高的同学可以进一步去读读测度论，从而拓展知识的宽度和深度。

3. 概率空间概念教学的应用案例

下面来举一些涉及概率空间的应用案例，通过引导学生对案例的分析、研究、思考和辩论，加深对概率思想的理解。

案例一甲、乙、丙三人参加面试抽签，每人的试题通过不放回抽签的方式确定。假设被抽的10个试题中有4个难题签，按甲、乙、丙次序抽签，试求甲抽到难题签，甲没抽到难题签而乙抽到难题签，甲、乙、丙都抽到难题签的概率。

解决问题都是依赖于所建立的概率空间，初等概率论往往不强调这一点，这容易在理解上造成误解。在这我们给出三种建立概率空间的方法：

解法一：设A、B、C分别表示甲、乙、丙抽到难题签的事件。将甲、乙、丙依次抽完试题看作一个实验，这时样本点对应于一个三元组 $\left\{a,b,c\right\}$，这里 $a,b,c$ 分别表示表示甲、乙、丙抽题情况，所有这样的三元组构成样本空间，这是古典概率模型，样本空间有 $10\ast 9\ast 8$ 个样本点，依次可以计算A包含 $4\ast 9\ast 8$ 个样本点， $\bar{A}B$ 包含 $6\ast 4\ast 8$ 个样本点，ABC包含 $4\ast 3\ast 2$ 个样本点，从而求得：

$P\left(A\right)=\frac{4}{10}$, $P\left(\bar{A}B\right)=\frac{6\ast 4}{10\ast 9}$, $P\left(ABC\right)=\frac{4\ast 3\ast 2}{10\ast 9\ast 8}$.

解法二：将甲、乙依次抽完试题看作一个实验，这时样本点对应于一个二元组 $\left\{a,b\right\}$，总共有 $10\ast 9$ 个样本点，依次可以计算A包含 $4\ast 9$ 个样本点， $\bar{A}B$ 包含 $6\ast 4$ 个样本点，从而求得：

$P\left(A\right)=\frac{4}{10}$, $P\left(\bar{A}B\right)=\frac{6\ast 4}{10\ast 9}$.

ABC不是这个样本空间的子集，不能直接在此模型下计算。

解法三：将甲抽完试题看作一个实验，这时样本点对应于一个单元组{a}，总共有 $10$ 个样本点，可以计算A包含 $4$ 个样本点，从而求得： $P\left(A\right)=\frac{4}{10}$。 $\bar{A}B$ 和ABC不是这个样本空间的子集，不能直接在此模型下计算。但可利用乘法公式得：

$P\left(\bar{A}B\right)=P\left(\bar{A}\right)P\left(B/\bar{A}\right)=\frac{6}{10}\ast \frac{4}{9}$ 和 $P\left(ABC\right)=P\left(A\right)P\left(B/A\right)P\left(C/AB\right)=\frac{4}{10}\ast \frac{3}{9}\ast \frac{2}{8}$。

这里的乘法公式中在条件下又单独建立了一维概率空间求条件概率。

通过以上分析可得，求P(AB)至少要建立两维空间，而乘法公式将高维空间要解决的问题转化到一维空间中去，从而简化了计算。一题多解使得学生对概率空间的概念更加深了理解。

案例二贝特朗悖论：在半径为1的圆内随机地取一条弦，问其长超过该圆内接等边三角形的边长 $\sqrt{3}$ 的概率等于多少？

这个问题有三种大家所熟悉的解法 [3]。很多人对这三种解法分析其合理性 [4] [5] [6] [7]。 [4] 中的结论认为只有解法一正确， [5] 中的结论是解法一和解法二正确， [6] 中的结论是三种解法都是合理的，这里通过建立概率空间的方法来分析其中的两种解法，则第三种解法就不言而喻了。

解法一：任何弦交圆周两点，因为对称性，先固定一点A在圆周上，以此点为一顶点作一等边三角形，另取一点B，确定一弦AB，只有B落在劣弧 $\stackrel{⌢}{CD}$ 上才能满足条件，端点B认为服从圆周上的均匀分布，所求概率等于 $\frac{1}{3}$ (见图1)。

解法二：因为对称性，固定一个方向，假定它们垂直于某一直径，认为其中心在直径上服从均匀分布，弦长只跟它与圆心的距离有关，因此当且仅当它与圆心的距离小于 $\frac{1}{2}$ 时，其长才大于 $\sqrt{3}$，因此所求概率为 $\frac{1}{2}$ (见图2)。

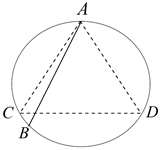
Figure 1. B is the uniform distribution on the circle

图1. B服从圆周上的均匀分布

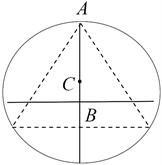
Figure 2. B is the uniform distribution on the diameter

图2. B服从直径上的均匀分布

这两种解法中对称性都没有严格地说清楚。先看解法一，任取圆周上两点可惟一确定一条弦，概率空间可取为二元组的集合 $\Omega =\left\{\left(a,b\right)\right\},a,b\in \left(0,2\pi \right]$，定义随机变量：

$X:\Omega \to R,\left(a,b\right)\mapsto a,Y:\Omega \to R,\left(a,b\right)\mapsto b,$

$X,Y$ 相互独立，都服从 $\left(0,2\pi \right]$ 上的均匀分布。记E为满足题目条件的样本点的集合，在两维的情况下P(E)不太好确定，利用下面的连续型全概率公式 [8] 转化一维情形。

定理设 $\xi ,\eta$ 是连续型随机变量， $\xi$ 的概率密度函数为 $f\left(x\right)$，则对于任意的博雷尔集F，有： $P\left(F\right)={\displaystyle {\int }_{-\infty }^{+\infty }P\left(F/\xi =x\right)f\left(x\right)dx}$。

$X$ 的密度函数为 $f\left(x\right)=\{\begin{array}{cc}\frac{1}{2\pi }& x\in \left(0,2\pi \right]\\ 0& 其它\end{array}$，对于 $x\in \left(0,2\pi \right]$，在 $X=x$ 条件下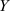，的条件密度函数为 $f_{Y/X}\left(y/x\right)=\{\begin{array}{cc}\frac{1}{2\pi }& y\in \left(0,2\pi \right]\\ 0& 其它\end{array}$，则 $P\left(E/X=x\right)=\frac{1}{3}$，根据上面定理可得： $P\left(E\right)={\displaystyle {\int }_0^{2\pi }\frac{1}{2\pi }}\ast \frac{1}{3}dx=\frac{1}{3}$。这里就利用概率空间的概念严格解释了解法1的正确性。

在解法二中意味着一条弦是由方向和弦的中点来确定，可以表达为二元组 $\left(\theta ,Q\right)$，其中 $\theta$ 为x轴正向与弦的夹角，Q表示弦的中点，因为通过圆心在任意方向存在弦，样本点的选取不是等可能的，这样建立概率空间表达弦的任意性是不合适的，第三种解法也是同样的道理。

4. 总结

概率空间是初等概率论中学习的第一个重要概念，所有的后续内容都是以此为出发点的，正确理解概率空间不仅是学好此门课的必备条件，也为后续课程高等概率论和随机过程的深度学习搭建了桥梁。在概率空间教学中，进一步在概率统计中对概念进行思辨教学有利于学生对问题的深入理解，有助于培养学生多维度思维能力和质疑，创新能力。

基金项目

北京理工大学教改项目(2019ZXJG046)。