1. 引言
在我们的日常生活中常见的物质形态是固态、液态和气态,而这些状态是由分子或者原子的集合形式所决定的。在这三种物态中分子或者原子不同的运动状况,让我们观察到了不同的特征。而另外一些固体,尽管在常温下有稳定的体积和形状,但它们内部的结构却更像是液体,我们称之为非晶态。而对于一些有机物质,不但有类似于晶体的光学性质,还有类似于液体的流动性,介于晶态和液态之间,我们称之为液晶态。
早在19世纪液晶现象就已经被人们发现,但直到20世纪50年代,人们才得以进一步地认识它的性质,逐渐建立起液晶理论。液晶态的物质在自然界当中也是广泛存在的,据统计,大约每200种有机化合物中就能发现一种液晶分子,相比于自然界中常见的气态、液态和固态,液晶态也被科学家称为第四态。生命系统中也普遍存在着液晶态结构。液晶就是晶体向液体过渡的中间相,它的内部粒子具有各向异性、取向有序、位置无序的特点。
液晶在现实生活中有着非常广泛应用,它们对光、电、磁和热都具有很高灵敏性,根据这一特点可以设计出各种各样具有热–光、磁–光、电–光等物理效应的仪器。鉴于它如此重要的应用背景,对于它的研究遍及了化学、物理学、生物学、材料科学和电子学,形成了各自专门的学科。例如液晶化学、液晶物理、生物液晶、液晶光学等,也引起了国内外数学家和物理学家们广泛的研究兴趣。液晶工业技术中最受重视的问题就是液晶中观察到的分子分布规律、缺陷、相变现象及其动力学规律,这些问题直接关系到液晶设备的制造。而适当的数学模型就是描述这些现象最有力的工具。上世纪50年代以来,数学家和物理学家先后建立了各种各样的数学模型。而针对现实中关注的问题,从数学的角度来看,我们关心的问题是相变的数学机理、动力学方程组解的整体存在性 [1] 和正则性以及强解的爆破准则 [2]。
2. 研究内容及研究方法
2.1. 研究内容
液晶方程在动力学中的重要性不言而喻,但很少对大初值有界区域液晶方程组进行数学分析,特别是大初值有界区域的液晶方程组强解的爆破准则是未知的。本课题研究的重点是,如果方程组具有大初值,且方程组是在有界区域内,则液晶方程组强解的是否会发生爆破现象 [3]。
2.2. 具体研究方法
首先,我们考虑Euler坐标下的大初值有界区域一维完全可压缩的液晶方程组:
(*)
其中
代表密度函数;
代表速度场;
代表单位的液晶光轴矢量(其中,
);压强
;且
是局部Lipschitz连续函数 (2.1.1)
考虑初始条件
,其中
恒为常数。 (2.1.2)
Ω是有界光滑区域,且
(2.1.3)
其中v是
的单位外法向量。
定理2.1.令 是(*)在初始条件(2.1.2)和(2.1.3)下的初值边界问题的一个强解,假设
满足条件(2.1.1),如果
是强解存在的关于时间的最大值,那么
是(*)在初始条件(2.1.2)和(2.1.3)下的初值边界问题的一个强解,假设
满足条件(2.1.1),如果
是强解存在的关于时间的最大值,那么
(2.1.4)
下面来证明定理2.1,
是(*)在初始条件(2.1.2)和(2.1.3)下的初值边界问题存在强解
的关于时间的最大值,
是(*)在
上的一个强解,其中
,但不是在
上的强解,假设(2.1.4)是错误的,那么有
(2.1.5)
目标是在(2.1.5)式成立的条件下,这个方程组的强解仍然存在,那么便可以说明
不是这个方程组强解存在的关于时间的最大值。
引理2.2.
是一个关于(*)在初始条件(2.1.2)和(2.1.3)下取得强解的关于时间的最大值,如果(2.1.5)式成立,那么对于任意的
,存在一个常数C,使得
(2.2.1)
证明:由(*)3式两边对x求导得:
(2.2.2)
在(2.2.2)式两边乘上
,并对所得方程在 上做关于x的积分得:
上做关于x的积分得:
(2.2.3)
又由
,且
。
所以
将
代入(2.2.3)式整理得:
利用(2.1.5)式,由Gronwall不等式,对于任意的
有:
证毕。
引理2.3.
是一个关于(*)在初始条件(2.1.2)和(2.1.3)下取得强解的关于时间的最大值,如果(2.1.5)式成立,存在一个常数C,使得
(2.3.1)
证明:在(2.2.2)式两边乘上
,并对所得方程在
上做关于x的积分得:
(2.3.2)
利用(2.2.1)式(r = 6),由Nirenberg’s interpolation不等式得:
(2.3.3)
又由
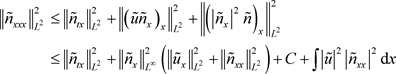 (2.3.4)
(2.3.4)
将(2.3.3)代入(2.3.4)得:
(2.3.5)
将(2.3.5)代入(2.3.3)得:
(2.3.6)
将(2.3.6)代入(2.3.2),利用(2.1)式,取
适当小得:
(2.3.7)
由Gronwall不等式,对于任意的
有:
(2.3.8)
证毕。
接下来我们将(2.3.8)结果回代到(2.3.5),利用(2.1.5)式我们得到
(2.3.9)
于是有
,进而得到
(2.3.10)
推理2.3.从(2.1.5)和引理2.2得到的 ,进而得
,进而得  ,另一方面,由(2.3.10)得
,另一方面,由(2.3.10)得 ,因此,由(*)3我们有:
,因此,由(*)3我们有:
(2.3.1)
接下来我们进行坐标变换 [4],设y为拉格朗日坐标,将拉格朗日坐标y和欧拉坐标x之间的坐标变换定义为
。其中
是由
所确定的映射,即:
定义函数 ;于是有
;又因为
,且
,
;于是
;于是有
;又因为
,且
,
;于是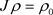 。
。
通过以上的变换我们就可以得到拉格朗日坐标下的液晶方程组:
(**)
且其初始条件为:
,
,其中
恒为常数。
P仍是局部Lipschitz连续函数,
变为
也仍是有界光滑区域,且
(3.1.1)
其中 是
的单位外法向量。
是
的单位外法向量。
(2.1.5)式变为
 (3.1.2)
(3.1.2)
3. 强解存在的定义
定义3.1. 给定一个时间
, 称为上述拉格朗日坐标下的液晶方程组(**)的一个强解,如果它满足以下条件:
称为上述拉格朗日坐标下的液晶方程组(**)的一个强解,如果它满足以下条件:
;
 ;
;
;
 ;
;
命题3.1. 方程组(**)存在系统的初始能量
,且J存在上界
和下界 。
。
证明:将(**)2两边乘上u,并对所得方程做关于y在
上的积分得:
(3.1.3)
又
;
再由(**)4得:
于是有:
(3.1.4)
将(**)3两边乘上
,并对所得方程做关于y在
上的积分得:
由
知,
于是
(3.1.5)
把(3.1.5)式代入(3.1.4)式得
 (3.1.6)
(3.1.6)
对(3.1.6)式关于t在
上积分得:
(3.1.7)
于是可以定义 为系统的初始能量。
为系统的初始能量。
然后来证明J存在上界:
由
得: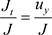 ,进一步有
,两边同时在
上积分得:
,进一步有
,两边同时在
上积分得:
,于是有
,定义J的上界为
。
接下来证明J存在下界:对(**)3有:
(3.1.8)
对(3.1.8)式关于t在
上积分,如何再对所得方程关于y在
上积分得:
令
得:
;于是:
于是
。
定义J的下界为
。
接下来,定义有效粘性通量G为
;
命题3.2. 有效粘性通量G有以下估计:
其中正常数C仅取决于
和
证明:由(**)3和(**)4可知:
(3.1.9)
方程两边同时乘以JG,并在
上做关于y的积分:
(3.1.10)
(3.1.11)
对
的估计,利用Gagliardo-Nirenberg不等式和Young不等式得:
(3.1.12)
对
的估计:
(3.1.13)
由
,
,J有上下界,于是有
。
对
的估计,利用Gagliardo-Nirenberg不等式和Young不等式得:
(3.1.14)
联立(3.1.9)~(3.1.12)得:
(3.1.15)
对(3.13)式两边关于t在[0, T]上积分,又由J有上下界可知:
(3.1.16)
由Gronwall不等式得:
(3.1.17)
再由Gagliardo-Nirenberg不等式:
(3.1.18)
其中
取决于
和
等。
命题3.3. 对于命题3.2.中的时间T,有如下估计:

其中C是正常数,且仅取决于
和
,但独立于
。
证明:
(3.1.19)
于是:
由
,
,J有上下界,于是有 。
。
于是有:
当 时:
时:
(3.1.20)
当 时:
时:
(3.1.21)
于是
(3.1.22)
又由
(3.1.23)
由(3.1.23)两边对y求导,并对所得方程两边乘以
,然后在R上做关于y的积分,利用Hölder不等式和柯西不等式得:
又由
而
,
,J有上下界,于是有
。
由
得
,
于是有
,
又由
,
,
,
,
,J有上下界,于是有
。
所以得到
再由Gronwall不等式得:
(3.1.24)
回头看G的定义,我们可以得到:
(3.1.25)
于是有:
进一步有:
(3.1.26)
由(3.23)可得:
于是有:
进一步有
(3.1.27)
其中C是正常数,且仅取决于
和
,但独立于
。
再回过头来去看G的定义,注意到
,又有:
(3.1.28)
又由
,
,J有上下界,可知
。
于是有
(3.1.29)
于是有
注意到:
再由Hölder不等式得:
(3.1.30)
于是可得:
其中C是正常数,且仅取决于
和
,但独立于
。
证毕。
上文已经知道 ,接下来由
,J有上下界知
,又
,接下来由
,J有上下界知
,又 得
。
得
。
,J有上下界知
,又
于是有
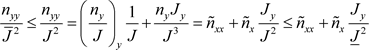
又由
,
,
得
至此定义3.1的所有要求均已满足,即
是拉格朗日坐标下液晶方程组(**)的一个强解,也就是说原液晶方程组(*)在满足(2.1.5)式条件下,仍然存在强解,则
不是原液晶方程组(*)强解存在的关于时间的最大值。这与
的定义相矛盾,因此(2.1.5 )式是错误的,定理2.1.的证明也就完成了。
4. 结论
大初值有界区域一维完全可压缩液晶方程组的强解存在爆破准则。