1. 引言
对于某一条新闻,在大众中会形成多种观点或立场,这种观点或立场称之为舆论。根据《中国互联网发展状况统计报告》 [1] 显示,截至2018年12月,中国网民数量已达8.29亿,舆论在网络中传播相比传统的媒体传播,其范围更加宽广。探索复杂网络系统中的舆情演化规律,为相关监管部门或组织提供有效管控,已成为国内外学者的研究方向。20世纪末,Watts [2] 发现大千世界中的复杂系统都有类似的网络拓扑结构属性,其中最突出的就是“六度分离”理论,基于此构建了小世界网络模型,并进一步发展出WS小世界模型和NW小世界模型 [3]。在这之后,Barabasi和Albert [4] 发现复杂网络系统中都具有“增长”和“优先链接”的特点,而且证明了互联网、电网等许多现实网络都具有这种“BA无标度网络”特性,这使得对网络模型的研究从以前的静态模型转到了动态的演化。随着现实复杂系统的发展,无标度网络已经不足以描述现实的网络,于是Yook S. H. [5] 在无标度网络的基础上衍生出了加权无标度网络,用以描述各连接边之间的差异性。
2. 信息流动与新闻的筛选
2.1. 相关定义与概念
物理学家将现实网络分为了四类,分别是生物网络、技术网络、信息网络和社会网络 [6]。实际上,信息网络和社会网络已经融合在一起,一方面表现为信息网络趋向社会化,另一方面体现在社会信息整体上的网络化。自然界中的系统大部分都可以归类到以上四种网络中,复杂网络现已成为研究这些系统的重要工具。
社会信息网络(SIN)中节点、边及其相关网络特性值的定义。
1) 节点:本文讨论的社会信息网络分为媒体节点和大众节点,分别用nm和np表示。媒体节点指在SIN中发布信息的媒介,如广播、电视、报社等;大众节点指在SIN中接受信息的传递者,即普通人。定义节点集合为N。
2) 边:两个节点之间可通过边连接。边表示信息通过某种媒介进行传播,这个媒介可以是手机、书信,也可以是面对面交谈等。本文讨论的SIN中有两类边,一类是连接媒体节点与大众节点间的边,用N中元素组成的无序对(nm, np)表示;另一类是连接大众节点与大众节点的边,用无序对(npi, npj)表示。定义边的集合为E。
3) 无向图:节点集合为N,边的集合为E,则图可以用有序二元组G = (N, E)表示。
4) 度:对于无向图G,与某节点相关联的边的条数为度。在SIN中,度描述了与某一个体取得联系的个体数量,反映了一个节点在网络中的重要程度。用TD(n)表示。
2.2. 新型媒体时期BA模型的建立
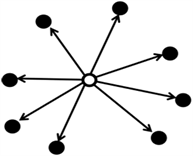
20世纪90年代,互联网用户开始从最初的军队和高校等科研机构普及到个人用户。1991年超文本的概念的引入 [7],同时催生了www的雏形以及配套的http传输协议。这些成果不仅是知识经济时代的开端,也是信息化时代的开端。以1990年为界,1990年之前为传统媒体时期,1990年至今为现代媒体时期。传统媒体传播的拓扑结构见图1(a)。
 (a)
(a)  (b)
(b)
Figure 1. Topological structure of traditional media and multimedia communication
图1. 传统媒体与多种媒体传播的拓扑结构
图1(b)中,空心点代表媒体节点,实心点代表大众节点。传统媒体的逻辑拓扑结构是星型结构,即以媒体节点为中心向各个方向传输。这种传播方式有以下特点:
1) 中心节点:中心节点作为信息来源,在传统媒体时代,对应着现实中的电视台、报社、电台。中心节点是传统媒体时代唯一的信息来源。
2) 单向流动:信息由信息源向信息接收者流动,即连接媒体节点与大众节点的边为有向边,从媒体节点指向大众节点。
3) 终端节点相互独立。大众节点之间无边连接,表明传统媒体时代,重大信息的发布仅通过传统媒体。中心节点将信息大量复制后单向流动至末端节点。这种单向传输的结构使得传统媒体在传统媒体时期享有舆论的主导权。对于传统媒体决定传播的信息,处于被动地位的接收者只能照单全收。同一时期,往往多种媒体共存,传播结构拓扑图见图2。
 (a)
(a)  (b)
(b)
Figure 2. Social information network in the period of traditional media and new media
图2. 传统媒体时期与新型媒体时期的社会信息网络
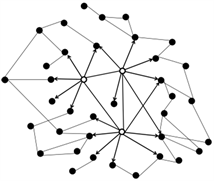
在传统媒体时期,当信息由媒体发布后,由接收到信息的人进一步传播,当信息从一个普通人传向另一个普通人时,信息并不是单向流动,而是双向传递交流的复杂过程,用单向边连接两个大众节点,来描述信息的扩散,就得到传统媒体时代的SIN图,见图2(a)。
新型媒体时期,由于互联网等新型媒介的加入,信息的发布和扩散都与传统时期有所不同。有以下特点:
1) 无中心化:由于新型媒介的加入,传统媒体的地位受到冲击,个人也开始享有发布信息的权力,过去传统媒体的主导权被弱化。
2) 双向流动:信息由发出节点传至到达节点,到达节点会反馈信息到发出节点。在传统媒体时期仅存在于大众之间的信息扩散过程中,现在也存在于媒体节点到大众节点的信息发布过程之中。
3) 孤立节点的数目更少。新型媒介使得两个连通节点间的路径更短,甚至为1。同时,任意连通的两点可以通过网络进行双向信息交流。
在新型媒体时期,除了以上特征,新型媒体时期还具有增长性和优先连接性。所谓优先连接特性,就是新节点与网络中较高的节点连接的概率更高,即“马太效应”,这使得网络中绝大多数节点的度较小,少数节点的度比较大。在这些特点的综合影响下,新型媒体时期的SIN更接近复杂网络中的无标度网络。不同于传统媒体时期节点度数较为均匀的泊松分布,无标度网络的节点度分布为幂律分布。即网络中节点度数为k的概率p(k)满足:
(1)
通过计算机模拟给出一个节点数为100的新型媒体时期SIN见图2(b)。
复杂网络理论表明,此类无标度网络往往具有小世界特性,这与现实比较吻合。以下主要基于新型媒体时期的无标度网络(BA)模型,对信息的传播和影响评估进行分析。
2.3. 新闻的过滤与筛选
依据新闻的定义,判断一条信息是否是新闻要考虑以下指标:
1) 真实性:若信息真实,a1 = 1;反之a1 = 0。
2) 流传度:对于某个节点数为N的网络,某条信息k在传播过程中经过的节点数为Nk,则该信息的流传度a2表示为:
(2)
3) 新颖性:若信息新颖,a3 = 1;反之a3 = 0。
新颖性可以用信息的搜索指数—热度来衡量。设t时刻信息的热度为H(t),该信息开始传播的时刻为初识时刻t0,当前时刻tnow的新颖度a3有:
(3)
用三个指标值的乘积
来衡量一条信息是否为新闻。若V = 1,该信息是新闻;若V = 0,该信息不是新闻。同时,流传度的定义表明,一条信息在大范围内(如省市)可能不是新闻,但在较小的地区(如学校)仍有可能成为新闻。
3. 基于染色模型的舆情分析
3.1. 影响力节点对舆论演变的影响
在一个无标度网络中,存在少数节点的介数显著高于大部分节点的介数,称这部分节点为影响力节点。在SIN中,影响力节点的一类代表是微博大V,他们的言论总会影响到不少人的判断,从而影响舆论的走向,即“权威暗示效应” [8] [9]。除了影响力节点对某一节点“观点”的影响,节点的相邻节点也会影响到节点“观点”的改变,即羊群效应。基于这两个效应,提出社会信息网络的染色模型,即用染色来模拟信息传播对公众观点的影响。
公众观点大致分为两类,一类是积极观点,另一类是消极观点。用白色节点代表积极观点,黑色节点代表消极观点,以上两种效应可以表述成以下的染色规则:
规则一:影响力节点的邻居节点,有80%的概率被影响力节点染色,如图3(a)。
 (a)
(a) 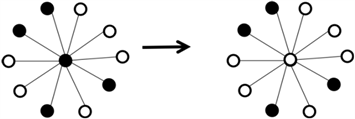 (b)
(b)
Figure 3. Dyeing rules satisfying herding effect and authority hint
图3. 满足羊群效应和权威暗示的染色规则
规则二:与影响力节点不相邻的节点,其周围节点持积极观点和消极观点的数目分别为n1和n2,若:n1 < n2,该节点被染为黑色;n1 = n2,该节点保持原色不变;n1 > n2,该节点被染为白色。规则二见图3(b)。
规则三:人群中有一定比例的“固执者”,这部分节点的颜色始终不改变;其他节点的颜色均有0.01的概率主动变色。
按照以上三条规则,建立基于无标度网络的染色模型,并用Matlab软件模拟上述染色过程。同时,分别统计白色节点和黑色节点的数目,计算两种节点的比例,就得到了持不同观点的节点比例。将比例作为因变量,时间作为自变量,就得到了积极观点和消极观点的比例随时间变化的图像。
初始条件下,两种观点的比例会小范围波动,对应着现实中舆论的传播阶段。在某一时刻改变了某一影响力节点的观点,对应着现实中某一微博大V发表了某些带有观点的言论,此时舆论会发生变化。运用染色规则,借助Matlab软件给出两种观点的比例随时间变化的图像见图4。
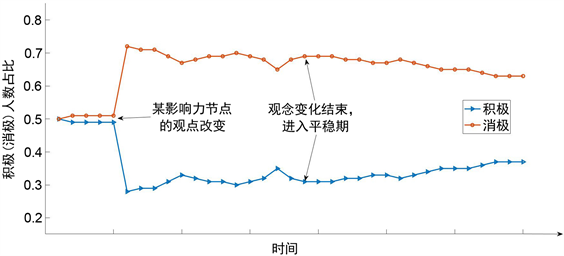
Figure 4. The influence of single influence node on public opinion
图4. 单一影响力节点对舆论的影响
在图4中,可以看出,最初舆论平稳时,两种观点的比例接近,当影响力节点的观点改变时(由积极观点转变为消极观点),舆论发生了较大变化。持消极观点的节点数比例增大。
在生活中有时会出现两方论战或者舆论反转的现象,这些现象的发生大多数情况是由于某些影响力节点发表了某些言论或进行“爆料”。现实生活中往往会发生多个影响力节点同时改变观点,以两个影响力节点的观点改变为例,研究多个影响力节点改变的情况。
考虑两种情况,一种是同一时刻有两个观点相反的影响力节点改变观点,另一种是两个观点相反的影响力节点先后改变观点。按上述三条染色规则进行Matlab仿真实验,得到如图5所示的结果。
 (a)
(a)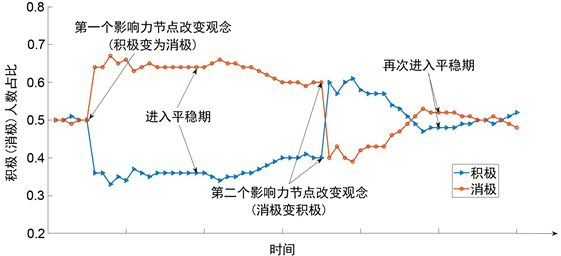 (b)
(b)
Figure 5. The influence of multiple influence nodes on public opinion
图5. 多影响力节点对舆论的影响
图5(a)表明,两个影响力节点在同一时刻改变,舆论的波动明显强于单影响力节点时舆论的波动,但比例的改变小于单影响力节点。由于介数较大(影响力更大)的节点转变为持消极观点,最终观念变化结束后,总体上持消极观点的比例较大。
图5(b)表明,两个影响力节点先后改变。首先是一个节点积极观点转变为消极观点,可看到,持消极观点的节点比例显著提高;当舆论进入平稳期后,另一个节点消极观点转变为积极观点,持消极观点的节点比例又会下降。最终回到平稳期。
通过上面的分析,可以看出,影响力节点的观点对大众观点以及舆论的变化起着不可忽视的作用。鉴于此,给出控制舆情的建议:重点关注影响力较大的节点其观点的改变。下面以媒体节点影响舆论进行分析。
3.2. 信息来源对舆论演变的影响
在新型媒体时代,互联网媒介的存在使得媒体节点在信息发布时的主导权受到了冲击,尤其是自媒体的兴起,使得个人也拥有了发布信息的权力。节点的度描述了某一节点与其他节点的连接情况,反映了节点的重要性。媒体节点是网络中度数较高的节点;大众节点包括了介数较高的影响力节点和一般节点。按上述三条染色规则进行Matlab仿真实验,可得到媒体节点和一般节点对舆论的影响结果,见如图6。
 (a)
(a) (b)
(b)
Figure 6. The influence of news sources on public opinion
图6. 消息来源对舆论的影响

Figure 7. The influence of initial views on public opinion
图7. 最初看法对舆论的影响
图6(a)所示是一般节点的观点改变时,舆论的改变情况,可以看到一般节点的观点改变基本不会影响到公众观点;图6(b)是媒体节点改变的舆论情况,可见,媒体节点的观点在舆论的改变中具有举足轻重的地位。
3.3. 最初看法对舆论演变的影响
R表示持积极观点人数的占比。图7为最初看法对舆论的影响。三种不同节点形状的折线,分别代表了初始时刻持积极观点节点的比例,依据染色规则二实现信息传播的过程中。当公共观点的最初看法不同时,也会对舆论的走向造成影响。
4. 结论
1) 管控网络中的影响力节点,诸如微博大V,巨大粉丝量的UP主等,有利于引导舆论的演变;
2) 即时对新闻热点做出回应,创造良好的初识舆论环境,可以有效防止舆论的失控;
3) 自媒体的兴起导致更多一般节点演化为影响力节点,因此互联网舆论的平衡脆弱易被打破,这也是当前舆情管控的难点所在。