1. 引言
期权定价问题是资产定价的主要研究内容之一。2015年上证50ETF期权正式推出,标志着我国金融衍生品市场迎来了“期权时代”,合理为期权定价对完善和发展我国金融衍生品市场有着重要的实践意义。
为了有效地给期权定价,标的资产的定价模型尤为重要。1900年Bachelier [1] 在其博士论文中首次提出用随机游动思想给出资产价格运行的随机模型。1965年Smuelson [2] 对该模型进行改进,假设股票价格服从几何布朗运动,从而避免了股票价格可能为负值的情形。1973年Black和Scholes [3] 在假设股票当前价格、时间、证券价格波动率和无风险利率都是客观变量且与投资者偏好不相关前提下,将所有投资者引向同一个以无风险利率作为投资回报率的风险中性世界 [4],并提出著名的B-S定价公式。然而,Fama [5] 等指出市场并不像想象那般完美,资产回报的分布呈现明显的“厚尾”现象,这与假设资产价格遵循几何布朗运动不相符。在许多对Black-Soles模型“常数波动率”进行改进的方法中,常见的是利用自回归条件异方差(GARCH)模型或随机波动率(SV)模型表示资产收益波动率的时变性和波动聚集现象等,其中随机波动率模型(SV)模型对波动率具有更好的样本内拟合表现以及样本外预测能力 [6]。
早期,Johnson和Shanno [7],Scott [8],Wiggins [9] 通过数值的方法系统地研究了SV模型。具体而言,Johnson、Shanno和Scott采用蒙特卡罗模拟,而Wiggins提出用有限差分法求解金融衍产品的期权等相应的PDE。但是由于缺乏封闭形式的解,这两种方法在实际计算过程中都会花费较长的时间,在应用方面存在局限性。1990年Hull和White [10] 提出Hull-White模型,在假设资产价格收益与波动率变动所遵循的布朗运动的相关系数为零的基础上推导出欧式期权定价公式。1991年Stein和Stein [11] 提出波动遵循Ornstein-Uhlenbeck过程,并导出欧式期权价格封闭形式的解,但该模型不能防止资产价格波动方差出现负值。1993年Heston [12] 应用均值回复平方根过程描述波动率方差过程,指出波动率满足非负性和均值回复性,并利用模型的仿射结构和反演定理方法给出欧式期权定价封闭形式的解,这保证了计算精度,防止利用数值解法产生的系统误差,且在参数估计方面封闭的解可以节省大量的时间和精力。Li [13] 研究了timer期权与Heston模型和贝塞尔过程有关的数学建模新方法,由于timer期权结果复杂,只得到了期权价格的半封闭形式的解。马俊美 [14] 等基于两类SV模型研究了欧式期权的价格和敏感性估计问题,在精确模拟算法基础上,讨论了舍取抽样技术在精确模拟算法中的有效应用。吴鑫育 [6] 等基于SV模型对上证50ETF期权定价,建立两步法来估计定价模型参数,该估计方法易于实现,只需单日期权数据即可进行估计,具有较高的估计效率。H Hong [15] 将SV模型应用于恒生指数的实际数据,研究了具有杠杆作用的SV模型在期权定价中的影响,结果显示随着期权到期日的增加,这种影响变得更加显著。谢超强 [16] 等研究了基于Heston模型和风险偏好视角的资产负债管理,应用随机控制方法,得到了该问题最优资产配置策略的解析表达式和相应值函数的解析解。Soleymani和Barfeie [17] 给出了随机波动率跳跃定价模型中空间变量离散点的非均匀生成,在这类模型下对美式和欧式期权的定价都是高效的,但需要讨论该数值方法的条件稳定性和离散方程全局收敛的充分条件。
Heston模型给出欧式期权定价封闭形式的解,有效提高参数估计方面的效力。但由于模型采用固定的均值回复平方根描述波动率过程,导致有时模型计算结果与实际有较大的误差。为了克服Heston模型的不足,本文设置动态的均值回复幂函数描述波动率过程,并根据具体的实际情况确定幂函数的具体形式,提高模型的适应性和计算精度。
2. Heston模型的改进
SV模型主要基于资产价格和波动率都遵循“有偏的随机游走”,即一个漂移项加上一个随机项 [1],且随机项服从标准的布朗运动。以下是考虑资产及其方差波动率都是随机过程的Stein-stein模型与Heston。
2.1. Stein-Stein [11] 模型
在滤子空间 上,文献 [11] 建立了stein-stein模型,其资产价格
上,文献 [11] 建立了stein-stein模型,其资产价格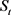 与瞬时波动率
分别满足如下SV模型
与瞬时波动率
分别满足如下SV模型
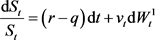
其中
和 分别表示资产和波动率的随机噪声,是相关系数为
的标准布朗运动,
分别表示资产和波动率的随机噪声,是相关系数为
的标准布朗运动, ,r表示资产回报率,q是红利率,
,r表示资产回报率,q是红利率,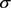 是
的波动率,
是均值回复水平,k是均值回复速率。
是
的波动率,
是均值回复水平,k是均值回复速率。
SV模型中含dt的项均为漂移项,含
项为随机项,例如,stein-stein模型中瞬时波动率的漂移项为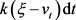 ,随机项为
,反映了波动率在该时刻先进行一个固定漂移再进行一定的随机变动。
,随机项为
,反映了波动率在该时刻先进行一个固定漂移再进行一定的随机变动。
2.2. Heston [12] 模型
Heston [12] 改进了stein-stein模型的随机项,提出如下随机波动率模型

其中
、 、
、
、
、 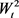 、r、q、
、r、q、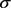 、k、
、k、 的意义同上。
的意义同上。
以上二个随机波动率模型都假设瞬时波动率 满足均值回复过程,且回复速率是一个常数。由于Stein-stein模型对刻画资产价格瞬时波动率方差过程欠充分,所以不能避免波动率出现负值的情况。虽然Heston应用均值回复平方根过程克服了波动率出现负值,但模型随机项中对
指数取确定的常数,有时导致定价结果与实际情况有较大差距。为此,本文在保留Heston模型的漂移项的基础数上,将随机项中
幂指数用待定参数表示,并根据实际情况确定参数的取值,有效提高模型定价的准确性。
满足均值回复过程,且回复速率是一个常数。由于Stein-stein模型对刻画资产价格瞬时波动率方差过程欠充分,所以不能避免波动率出现负值的情况。虽然Heston应用均值回复平方根过程克服了波动率出现负值,但模型随机项中对
指数取确定的常数,有时导致定价结果与实际情况有较大差距。为此,本文在保留Heston模型的漂移项的基础数上,将随机项中
幂指数用待定参数表示,并根据实际情况确定参数的取值,有效提高模型定价的准确性。
2.3. 改进的Heston模型
在滤子空间 上,假设资产价格
与瞬时波动率
上,假设资产价格
与瞬时波动率 满足如下新的SV模型
满足如下新的SV模型

(2-1)
其中 、
、r、q、
、
、r、q、 、k、
的意义同上, α ,β 为待定参数,且满足
、k、
的意义同上, α ,β 为待定参数,且满足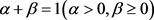 。
。
显然,当 时,模型(2-1)即为Stein-stein模型;当
时,模型(2-1)即为Heston模型。
时,模型(2-1)即为Stein-stein模型;当
时,模型(2-1)即为Heston模型。
3. 改进Heston模型下欧式看涨期权的PDE
下面利用∆-对冲原理 [18] 推导模型(2-1)下的欧式看涨期权的PDE。为了方便,将
、
分别简记为S、v,假设资产组合 由一单位的方差期权V,∆单位的资产S和
由一单位的方差期权V,∆单位的资产S和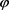 单位的其他期权G组成,为了让形式更加简洁假设支付的红利为0。则资产组合
单位的其他期权G组成,为了让形式更加简洁假设支付的红利为0。则资产组合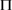 的价值变化为
的价值变化为
 (3-1)
(3-1)
根据模型(2-1),由伊藤引理 [19] 得
(3-2)
(3-3)
将(2-1)、(3-2)与(3-3)代入(3-1)整理化简得
(3-4)
根据无风险资产的假设,(3-4)右端最后两项系数均为零,即
解得
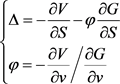 (3-5)
(3-5)
根据无套利原则 [19] 有 ,于是由(3-4)有
,于是由(3-4)有
(3-6)
将(3-5)代入(3-6)整理化简得
(3-7)
可以看出,(3-7)左右两侧分别是关于期权价格V和G的函数,且形式相同,根据Heston [12] 方程左右两边都可以用同一个形式的函数如 来表示,即
来表示,即

且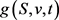 满足
满足

式中
反映波动风险的价格,是波动率的线性函数,即
,
为常数,将其代入(3-8)得
为关于v的线性函数,为了更加简洁,记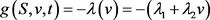 ,其中
,
将其代入(3-8)整理化简得到改进Heston模型下期权价格的PDE为
,其中
,
将其代入(3-8)整理化简得到改进Heston模型下期权价格的PDE为
(3-9)
并且(3-9)满足以下边界条件
 ,
,
其中T为到期日,K为执行价格。
当资产为零,买入期权就毫无价值;当资产价格上涨时delta接近1;当波动率增加时,买入期权就
等于资产价格,即分别对应有 ,
,和
,
,和 。
。
记
,代入(3-9)整理化简得
(3-10)
显然(3-10)与(3-9)是等价的。
4. 改进Heston模型下欧式看涨期权定价公式
根据文献 [18] 知(3-10)的解为
(4-1)
和 分别表示欧式看涨期权按照股票价格行权的概率和在风险中性环境被行权的概率。
分别表示欧式看涨期权按照股票价格行权的概率和在风险中性环境被行权的概率。
下面确定(4-1)中 和
。
和
。
首先将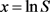 代入(4-1)得
代入(4-1)得
(4-2)
(4-2)式分别求以下偏导数得
 ,
,
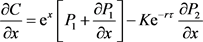 ,
,
,
, (4-3)
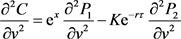 ,
,
。
将(4-3)代入(3-10)整理化简得
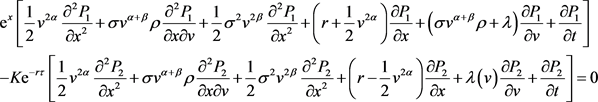
记
,
, ,则上微分方程可化为
,则上微分方程可化为
(4-4)
(4-4)是 满足的偏微分方程,下面通过随机变量x的特征函数给出。
满足的偏微分方程,下面通过随机变量x的特征函数给出。
根据如下反演定理知,可通过x的特征函数给出
。
引理1 [20] (反演定理)若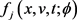 是随机变量x的特征函数,则
是随机变量x的特征函数,则
 (4-5)
(4-5)
其中 为虚数单位,
为实数。
为虚数单位,
为实数。
因此,为了确定
,下面将推导特征函数 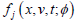 的计算式
。
的计算式
。
根据文献 [18],随机变量x的特征函数为如下对数形式
 (4-6)
(4-6)
其中
与
是独立于x和v的函数,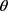 为待定参数,
为待定参数,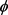 为实数。
为实数。
根据Feynman-Kac定理 [19],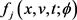 与
有相同的PDE,因此
与
有相同的PDE,因此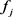 满足(4-4)。当
即
时,
已知,
为常数,期望是其本身,即边界条件
满足(4-4)。当
即
时,
已知,
为常数,期望是其本身,即边界条件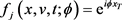 ,此时
,此时 ,
,  。
。
对(4-6)式分别求以下偏导数
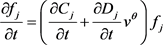 ,
,
,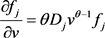 ,
,
 ,
,
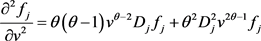 ,
,
。
因为
满足(4-4),所以将上述偏导数代入(4-4)式化简得
(4-7)
下面将证明
、 ,以及确定
,以及确定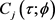 与
的计算式。
与
的计算式。
1) 因为当 时
时 ,所以(4-7)可化为
,所以(4-7)可化为
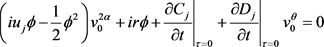 (4-8)
(4-8)
假设 ,由于(4-8)对任意
,由于(4-8)对任意 恒成立,故
恒成立,故 的系数为零,即
。于是
的系数为零,即
。于是 或
或 。而
显然不恒为零,故
。而
显然不恒为零,故 ,即
,即 为复数,这与
为复数,这与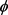 为实数矛盾。因此
。
为实数矛盾。因此
。
2) 将
代入(4-8)得
 (4-9)
(4-9)
i) 若 ,则(4-9)化为
,则(4-9)化为
(4-10)
假设
时,由于(4-10)对任意v恒成立,故v与v0的系数都为零,从而(4-10)可化为
解得
或 ,这与
,这与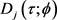 与
与 有关相矛盾。所以,当
时,必有
,此时新SV模型即是Heston模型。
有关相矛盾。所以,当
时,必有
,此时新SV模型即是Heston模型。
ii) 若 。假设
。假设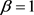 ,则(4-9)化为
,则(4-9)化为
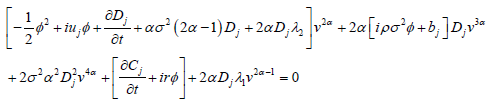 (4-11)
(4-11)
由于(4-11)对任意v恒成立,故 与
与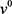 的系数都为零,(4-11)可化为
的系数都为零,(4-11)可化为
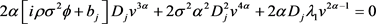
解得 或
或 ,这与
与
,这与
与 有关相矛盾。因此有
。
有关相矛盾。因此有
。
假设 且
且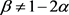 且
且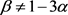 ,而
且
,而
且 且
,则
且
,则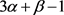 ,
,
,
,
,
均不等于0且不等于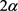 。由于(4-9)对任意v恒成立,故
。由于(4-9)对任意v恒成立,故 与
与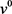 的系数都为零,(4-9)可化为
的系数都为零,(4-9)可化为
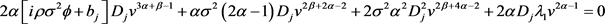
解得 或
或 ,这与
,这与 与
与 有关相矛盾。
有关相矛盾。
因此,在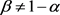 ,
,  ,
中至少有一个不成立。
,
中至少有一个不成立。
若 ,将其代入(4-9)得
,将其代入(4-9)得
(4-12)
由于(4-12)对任意v恒成立,故 与
与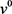 的系数都为零,(4-12)化为
的系数都为零,(4-12)化为
(4-13)
当
时,(4-13)可化为
(4-14)
由于(4-14)对任意v恒成立,故
与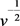 的系数都为零,从而
的系数都为零,从而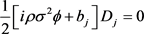 ,
, 或
,
或
, 与
与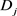 与
与 有关矛盾,
有关矛盾, 与
与 是实数矛盾。
是实数矛盾。
当
时,由于(4-13)对任意v恒成立,故 的系数零,(4-13)化为
的系数零,(4-13)化为
解得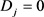 或
或 ,
,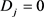 与
与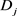 与
与 有关矛盾,而
有关矛盾,而 与
与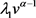 为实数矛盾。
为实数矛盾。
因此, 。
。
若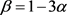 ,将其代入(4-9)得
,将其代入(4-9)得
(4-15)
由于(4-14)对任意v恒成立,故 与
与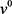 的系数都为零,(4-14)可化为
的系数都为零,(4-14)可化为

解得 或
或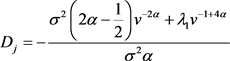 ,这与
与
,这与
与 有关相矛盾。
有关相矛盾。
综上所述有 不成立,即有
不成立,即有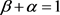 。
。
接下来确定 与
的计算式。
与
的计算式。
将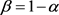 代入模型(2-1),(2-1)可转化为如下形式
代入模型(2-1),(2-1)可转化为如下形式
 (4-16)
(4-16)
当 时,(4-16)即为Heston模型,欧式看涨期权定价公式采用Heston模型下欧式看涨期权定价公式。
时,(4-16)即为Heston模型,欧式看涨期权定价公式采用Heston模型下欧式看涨期权定价公式。
当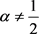 时,将
代入(4-9)得
时,将
代入(4-9)得
(4-17)
由于(4-17)对任意v恒成立,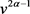 的系数为0,即
。
的系数为0,即
。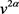 的系数和常数项都为零,因此可由(4-17)得
的系数和常数项都为零,因此可由(4-17)得
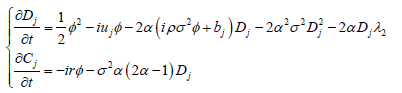 (4-18)
(4-18)
根据文献 [18] 求解(4-18)的Riccati方程得到
与
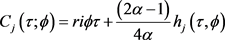 ,
,
 ,
,
其中,
,
 ,
,
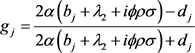 。
。
综合以上推导可得新SV模型下欧式看涨期权价格封闭解为
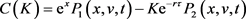 (4-19)
(4-19)
其中
,
,
,
,
 ,
,
 ,
,
,
,
,
,
。
5. 数值计算实例
为了说明本文提出模型的可行性和有效性,以上证50ETF看涨期权2015至2018年四年的历史数据为例(数据来自wind数据库),将本文提出的改进Heston模型与Heston模型隐含波动率进行比较。主要采用计算软件Matlab2018b和Stata14,根据这四年上证50ETF看涨期权的历史数据,采用文献 [18] 中参数估计方法MLE,分别得到模型的参数取值如下表1。
选取2015至2018年上证50ETF看涨期权中最常见的到期日(27天、77天、127天、177天)在不同执行价格的数据,分别计算其市场隐含波动率、Heston模型隐含波动率和改进Heston模型隐含波动率,并绘制图1。
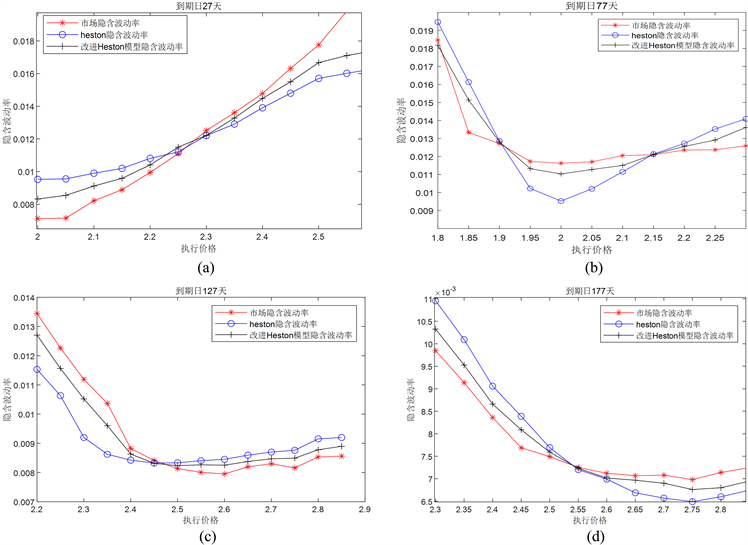
Figure 1. Implied volatility chart of Shanghai 50ETF European call options
图1. 上证50ETF欧式看涨期权隐含波动率图
其中图1(a)为上证50ETF欧式看涨期权初始时间2016年5月19日,股票指数开盘价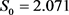 ,到期日27天的欧式看涨期权相应的隐含波动率情况;图1(b)为初始时间2015年6月17日,上证50ETF开盘价
,到期日77天的欧式看涨期权相应的隐含波动率情况;图1(c)为初始时间2017年8月16日,上证50ETF开盘价
,到期日27天的欧式看涨期权相应的隐含波动率情况;图1(b)为初始时间2015年6月17日,上证50ETF开盘价
,到期日77天的欧式看涨期权相应的隐含波动率情况;图1(c)为初始时间2017年8月16日,上证50ETF开盘价 ,到期日127天的欧式看涨期权相应的隐含波动率情况;图1(d)为初始时间2018年12月24日,上证50ETF开盘价
,到期日177天的欧式看涨期权相应的隐含波动率情况。从拟合情况来看,各种不同到期日下改进Heston模型都比Heston模型有更好的拟合效果。
,到期日127天的欧式看涨期权相应的隐含波动率情况;图1(d)为初始时间2018年12月24日,上证50ETF开盘价
,到期日177天的欧式看涨期权相应的隐含波动率情况。从拟合情况来看,各种不同到期日下改进Heston模型都比Heston模型有更好的拟合效果。
6. 结论
传统的Heston模型与stein-stein模型中有一些常数性假设,本文假设这些常数为可变参数得到改进的Heston模型。首先利用∆-对冲原理构造无风险资产,给出了该模型下期权价格满足的PDE方程;其次对模型参数进行了一些合理限制,并对限制条件加以证明,利用反演定理得到期权价格的封闭式解,说明该模型具有分析可处理性,并得出当参数取一定值时,Heston模型与stein-stein模型是该模型的一种特例。最后以上证50ETF看涨期权2015年至2018年四年的历史数据为例,对比了该模型与Heston模型对市场隐含波动率的拟合情况,得到该模型比Heston模型有更好的拟合效果。
基金项目
广西重点研发计划项目(桂科AB17292095);广西研究生教育创新计划项目。