1. 引言
城市河流是城市重要的自然资源和环境载体 [1],是城市生态环境的重要组成部分,可为城市提供诸多社会和经济服务 [2]。随着城市化进程的加速,水资源日趋紧张,同时由于工业废水与生活污水的排放,导致许多城市的河流水质污染严重,生态功能退化。城市河流的污染问题越来越受重视,针对城市河流水质问题开展的研究也越来越多,如Kannel等 [3] 利用4种水质指数评估尼泊尔Bagmati河流域的水质时空变化特性;Oginni [4] 对尼日利亚Atuara河城区内河段的常规水质参数以及重金属等污染物浓度进行观测,并评估其河水水质;Brion等 [5] 引入流域尺度评价方法研究污水处理对小型城市河流系统水质的影响;Glińska-Lewczuk等 [6] 对波兰北部Lyna河城市化,环境变量,物理化学和微生物学数据进行了检验,研究了五个城镇对河流水质的影响。在河流水质模拟研究方面,李如忠等 [7] 提出了运用未确知数学理论进行河流水质模拟预测的未确知数学模型,该模型可计算河流污染物预测浓度区间及其对应的主观可信度;武周虎 [8] 对河流移流离散水质模型进行简化,并对分类判别条件进行分析;刘悦忆等 [9] 建立了基于蒙特卡洛模拟的水质概率预报模型,该模型可统计分析计算时段内河流水质的范围及其概率。由以上研究实例可知,对城市河流水质时间变化特性及结合水质模型对河流水质进行模拟预测的研究是当前及未来一段时间内水文与水资源领域的研究热点之一。
自2014年中国大运河成功入选世界文化遗产名录以来,大运河文化带建设成为国家文化战略的重要组成部分,对大运河生态环境的保护越来越受到重视。扬州市古运河是大运河的开端,是大运河最古老的一段 [10]。古运河连通扬州城区多条河道,在扬州市排水、航运、旅游等方面发挥重要作用。随着扬州市工业的发展,古运河沿河建立了数十家工业企业单位,其中扬农化工厂由于存在时间较长,排污量较大,对河段水质的影响较大,在化工厂下游约200 m为运河三湾风景区。为揭示古运河三湾河段的水质时间变化特性,本文选取古运河三湾风景区河段为研究区,对其水质参数与
浓度进行观测,分析其时间变化特性,并构建污染物随流分散模型对该河段的
运移过程进行数值模拟,以期为古运河水质和水生态的研究提供部分基础数据,以及为城市河流水质监测及污染物运移过程的数值模拟提供方法上的参考。
2. 材料与方法
2.1. 研究区概况与水质观测
选取古运河三湾风景区河段为研究区,在该河段干流的入口断面(P1:32˚22'20.37''N,119˚25'0.42''E,在化工厂排污口下游约200 m)与出口断面(P2:32˚21'20.75''N,119˚25'26.83''E)及两条支流的入口断面(二桥河P3:32˚21'39.94''N,119˚25'11.67''E;七里河P4:32˚21'48.56''N,119˚25'34.31''E)进行常规水质参数与离子浓度的观测(图1)。利用多参数水质分析仪(型号:YeoKal 615;产地:澳大利亚)对各断面的水温WT (℃)、pH、溶解氧浓度DO (mg/L)、电导率EC (μS/cm)进行一周2次的观测;每2周采集一次各断面的水样,利用多参数离子分析仪(型号:HydrionX;产地:荷兰)对水体中的
浓度进行测量,观测时段为2018年10月至2019年6月。
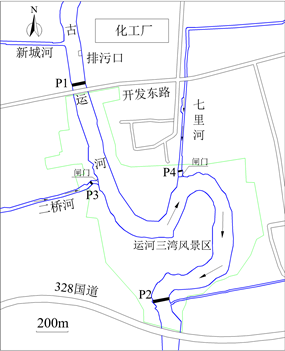
Figure 1. Sketch map of the study river reach and the observation sections
图1. 研究河段及观测断面示意图
2.2. 研究方法
2.2.1. 变异系数法
变异系数是衡量样本分布离散程度的参数,变异系数越大,样本分布越离散,波动程度越大。权重反映评价因子对水体污染的贡献,是评价结果是否合理的决定性因素之一 [11]。变异系数法根据指标数据求权重,是一种客观求权重的方法 [12]。变异系数及权重的计算公式如下:
(1)
(2)
式中S为某一水质指标的标准差,
为该水质指标的均值,V为该参数的变异系数,Ai为第i项指标的权重,Vi为该指标的变异系数。
2.2.2. 单因子水质标识指数法
由徐祖信提出的单因子水质标识指数法 [13],不仅可以完整地表示水质类别、水功能区目标等重要信息,还可以定量地评价水质状况,揭示水质的污染程度 [14]。溶解氧是衡量水体环境的重要指标之一,是维持健康的水生生态系统的关键因素 [15],因此选取DO作为单因子水质标识指数法的评价指标,其计算公式如下:
(3)
式中X1为以DO为指标的水质类别,根据《国家地面水环境质量标准》(GB3838-2002)中的水质类别划分标准,确定X1,若水质类别为I类,则X1为1,以此类推。
X2的计算公式为:
(4)
式中
为第k类水质的上边界值,
为第k类水质下边界值,
为DO的实测浓度。
当水质劣于Ⅴ类水时,计算公式为:
(5)
m为计算修正系数,一般取4。
X3为水质类别与功能区规划设定类别的比较结果,为一位或两位有效数字。若水质类别好于或达到水环境功能区类别,则X3取0;若水质类别比功能区类别差且X2不为0,则
(6)
若水质类别比功能区类别差且X2等于0,则
(7)
式中fi为水环境功能区类别。
2.2.3. 多元线性回归法
多元线性回归法利用线性拟合多个自变量与因变量的关系,确定多元线性回归方程的参数,通过回归方程预测因变量的趋势 [16]。DO与WT、pH、水生生物、悬浮物等因素有重要的关系 [17],因此本研究以DO为因变量(Y),研究自变量WT (X1)、pH (X2)对DO影响,计算过程如下:
建立多元线性回归方程
,其中Y、X1、X2分别为DO、WT和pH实测序列,回归方程以矩阵形式表示为Y = XB,其中
,
,
计算中间变量
(8)
(9)
(10)
(11)
(12)
建立矩阵方程
(13)
解得b1,b2值,根据公式
计算b0,最终获得DO与WT、pH的多元线性回归模型。采用R检验法对自变量与因变量的相关性进行检验,R值越接近1,相关性越显著,模型能更好地反映自变量与因变量之间的相关性。R检验法的计算公式如下:
(14)
2.2.4.
运移过程数值模拟
结合水流连续性方程(15)、河流污染物随流分散方程(16),构建研究河段一维河流水文水质模型,模型的主要方程式如下所示:
(15)
(16)
式中h为计算断面平均水深(m),q为断面单宽流量(m2/s);u为断面平均流速(m/s),C为污染物离子(NH4+)浓度(mg/L),Kx为河流纵向分散系数,K为污染物降解系数。
河流纵向分散系数Kx采用Fischer等 [18] 提出的经验公式进行计算:
(17)
(18)
式中h为断面平均水深(m),u*为断面的摩阻流速(m/s),W为断面的河宽(m),u为断面平均流速(m/s)。
对水流连续方程(15)与河流纵向分散方程(16)进行差分计算,计算公式如下:
(19)
(20)
(21)
计算过程基于Fortran语言编程实现。本研究利用该模型模拟研究河段
的随流扩散过程,并通过纳什效率系数(NSE)对模型的模拟精度进行评价,计算公式如下:
(22)
其中
为t时刻的实测值,
为t时刻的模拟值,
为实测值的均值。NSE值越接近1,模型的模拟精度越高;NSE越接近0,则模型模拟结果越接近观测值平均水平,模拟结果总体可信;若NSE远小于0,则模拟结果不可信。
3. 结果与分析
3.1. 观测结果
研究河段干流观测断面(P1、P2) WT与DO的观测结果如图2所示,pH与EC的观测结果如图3所示(2019年1月21日至2019年2月24日期间数据欠测):
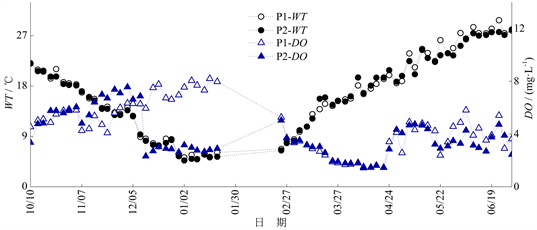
Figure 2. The change process of WT and DO in P1 and P2 sections (2018/10/10-2019/6/30, there was no observation in February, 2019)
图2. P1、P2断面WT和DO变化过程(2018/10/10~2019/6/30,2019年2月数据欠测)
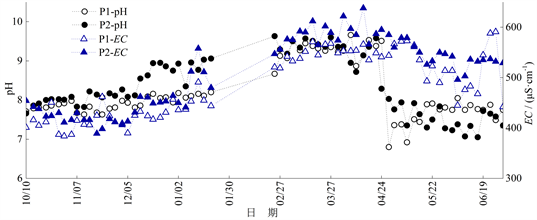
Figure 3. The change process of pH and EC in P1 and P2 sections (2018/10/10-2019/6/30, there was no observation in February, 2019)
图3. P1、P2断面pH与EC变化过程(2018/10/10~2019/6/30,2019年2月数据欠测)
如图2所示,2018年10月至2019年1月WT呈下降趋势,2019年3月至6月WT逐渐上升,最高为29.8℃ (2019年6月23日),最低为5.0℃ (2019年1月9日);2018年10月至11月P1、P2断面DO较为接近;2018年12月P2断面DO有较大幅度的下降,而P1断面的DO没有明显的变化,2018年12月至2019年1月P2断面DO明显低于同期的P1断面;2019年3月至4月P1、P2断面DO较为接近且均呈下降趋势;2019年5月至6月P1、P2断面DO有所上升,且在2 mg/L~6 mg/L之间波动。
由图3可知,2019年2月之前与2019年3月至4月P1、P2断面的pH和EC均呈上升趋势,由于P1断面不受河段支流(二桥河、七里河)排水的影响,说明该时段干流的pH和EC受化工厂排污的影响而升高;2019年5月至6月干流的pH与EC呈下降趋势,且图2显示该时段内P1、P2断面的DO有所上升,说明该时段内干流河段的水质状况有所好转;大部分时段内P2断面同期的pH和EC均高于P1断面。
支流观测断面(P3、P4)WT与DO的观测结果如图4所示,pH与EC的观测结果如图5所示(2019年1月21日至2019年2月24日期间数据欠测):
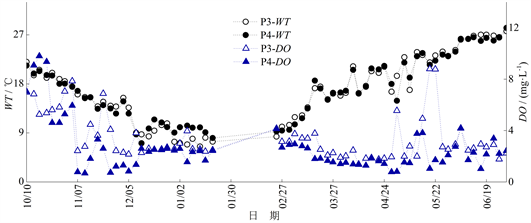
Figure 4. The change process of WT and DO in P3 and P4 sections (2018/10/10-2019/6/30, there was no observation in February, 2019)
图4. P3、P4断面WT和DO变化过程(2018/10/10~2019/6/30,2019年2月数据欠测)
由图2、图4可知,研究期间支流断面WT的变化过程与干流相似;2018年11月至2019年1月与2019年3月至4月,P3、P4断面的DO呈下降趋势;对比图2、图4的DO变化过程可知,2018年11月至2019年1月与2019年3月至4月P2断面DO变化趋势与P4断面较为接近,表明该时段内P2断面DO受P4断面排水的影响而降低;2019年5月至6月P3、P4断面DO在1 mg/L~4 mg/L之间波动;大部分时段P3断面同期的DO高于P4断面;研究期间支流(二桥河、七里河)水体颜色发黑,属于黑臭水体,其观测断面的DO大部分时段低于4 mg/L,水质类别劣于III类水。
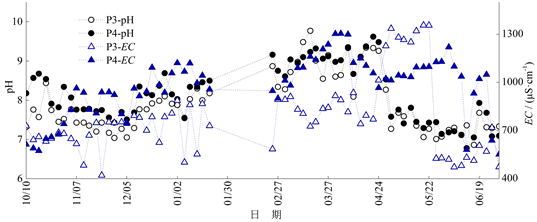
Figure 5. The change process of pH and EC in P3 and P4 sections (2018/10/10-2019/6/30, there was no observation in February, 2019)
图5. P3、P4断面pH与EC变化过程(2018/10/10~2019/6/30,2019年2月数据欠测)
由图5可知,2018年11月至2019年1月与2019年3月至4月P3、P4断面pH呈上升趋势,2019年5月至6月pH有所下降;2019年5月之前EC总体呈上升趋势,且大部分时段P4断面同期的pH与EC均高于P3断面;2019年6月P3断面EC有较大幅度的下降,其原因是该时段二桥河闸门打开,向干流排水,但由于二桥河流量较小,排水并未引起干流EC的明显变化;观测时段内EC波动程度较大,P3断面EC变化范围为421 μS/cm (2018年11月21日)~1227 μS/cm (2019年4月28日),P4断面EC变化范围为574 μS/cm (2018年10月17日)~1304 μS/cm (2019年4月3日),EC反映水中可溶性固体的总量,可作为水体盐度的度量指标 [19],由此可推断支流水体中溶解固体量较多。
3.2. 变异性分析
观测时段包含两个完整的季度(2018年10月至12月、2019年4月至6月),以季度为时段,计算各断面水质参数的季度变异系数、总变异系数及权重,结果如表1、表2所示。

Table 1. Quarterly coefficient of variation, overall coefficient of variation and weight of WT and EC in each section
表1. 各断面WT与EC季度变异系数、总体变异系数与权重
注:2019年2月无观测数据,未计算2019年1~3月的变异系数。

Table 2. Quarterly coefficient of variation, overall coefficient of variation and weight of DO and pH in each section
表2. 各断面DO与pH季度变异系数、总体变异系数与权重
注:2019年2月无观测数据,未计算2019年1~3月的变异系数。
由表1、表2可知,4个观测断面WT同期的变异系数相差不大,且2018年第四季度的变异系数较大,WT的总变异系数从大到小依次为P1 > P2 > P3 > P4;P1、P2断面的EC的季度变异系数均小于0.1,说明这两个季度干流断面的EC波动程度较小,而大部分时段P3、P4断面同期的EC的季度变异系数大于P1、P2断面,说明支流断面EC的波动程度大于干流断面,EC的总变异系数从大到小依次为P3 > P4 > P2 > P1;各断面DO不同时段的变异系数差异较大(0.173~0.796),P3、P4断面同一季度的变异系数均大于P1、P2断面,说明P3、P4断面DO的波动程度较高,DO的总变异系数从大到小依次为P4 > P3 > P2 > P1;各断面pH的季度变异系数较小(0.019~0.114),说明pH的波动程度较小,pH的总变异系数从大到小依次为P3 > P2 > P4 > P1;根据总变异系数推求的权重可知,研究期间各水质参数对水质变化的贡献从大到小依次为DO > WT > EC > pH。
3.3. 单因子水质标识指数分析
P1、P2断面以DO为指标的单因子水质标识指数计算结果如图6、图7所示。
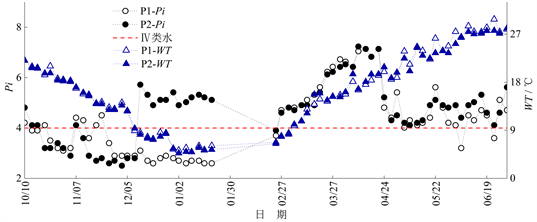
Figure 6. The change process of WT and single factor water quality identification index (Pi) in P1 and P2 sections (2018/10/10-2019/6/30, there was no observation in February, 2019)
图6. P1、P2断面WT与水质标识指数(Pi)变化过程(2018/10/10~2019/6/30,2019年2月数据欠测)
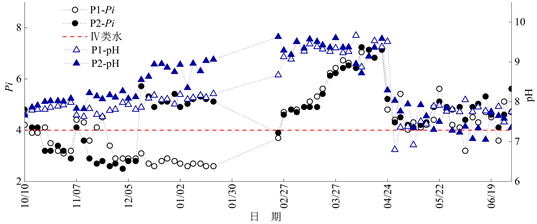
Figure 7. The change process of pH and single factor water quality identification index (Pi) in P1 and P2 sections (2018/10/10-2019/6/30, there was no observation in February, 2019)
图7. P1、P2断面pH与水质标识指数(Pi)变化过程(2018/10/10~2019/6/30,2019年2月数据欠测)
由图6、图7可知,在2018年10月至11月期间,P1、P2断面的水质标识指数Pi多小于4,即水质类别为I、II或III类水,满足扬州市古运河水功能区水质目标(III类水),且P2断面同期水质略好于P1断面;2018年12月至2019年1月,P2断面Pi明显上升,水质类别劣于Ⅲ类水,部分时刻甚至达到劣V类水,而P1断面水质类别未出现较大变化,由对P1、P2断面DO观测结果的分析可知,该时段内P2断面受支流排水影响导致DO下降,而P1断面未受支流排水影响,因此该时段内P1断面同期的水质类别优于P2断面;2019年3月至4月,P1、P2断面Pi较为接近且均呈上升趋势,水质类别多为V类或劣V类,其原因是支流闸门关闭后支流排水的影响逐渐消失,因此两断面的Pi逐渐接近同一水平,但该时段内两断面同时受到上游化工厂排污的影响,因此其Pi上升,水质变差;2019年5月至6月pH与Pi有所下降,P1、P2断面水质多为IV类水。
P3、P4断面以DO为指标的水质标识指数Pi变化过程如图8、图9所示。
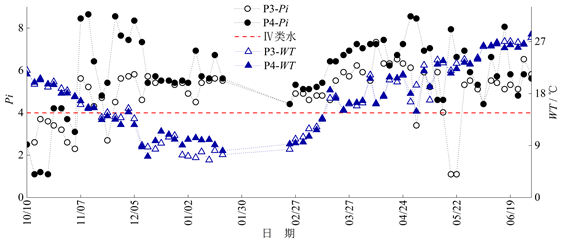
Figure 8. The change process of WT and single factor water quality identification index (Pi) in P3 and P4 sections (2018/10/10-2019/6/30, there was no observation in February, 2019)
图8. P3、P4断面WT与水质标识指数(Pi)变化过程(2018/10/10~2019/6/30,2019年2月数据欠测)
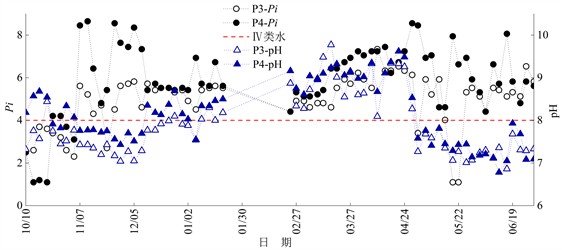
Figure 9. The change process of pH and single factor water quality identification index (Pi) in P3 and P4 sections (2018/10/10-2019/6/30, there was no observation in February, 2019)
图9. P3、P4断面pH与水质标识指数(Pi)变化过程(2018/10/10~2019/6/30,2019年2月数据欠测)
由图8、图9可知,2018年10月P3、P4断面水质基本达到III类水的水质目标,但2018年10月之后的时段P3、P4断面水质多为IV、V或劣V类水,其中P4断面水质为劣V类水的时段所占的比例最大(46.3%),2018年11月与2019年4月至6月的某些时段P4断面的Pi甚至达到8以上;大部分时段内P4断面同期的pH与Pi均高于P3断面,说明P4断面受污染程度更高,水质更差;对比P2、P4断面的Pi可知,2018年12月至2019年1月与2019年3月至4月两断面的Pi较为接近,其原因是P4断面排水对P2断面的Pi产生了影响;由于P3、P4断面的水体为黑臭水体,受沿河工业生活污水的随机排放的影响较大,因此其Pi与pH的变化随机性较强。
3.4. 多元线性回归分析结果
各断面的多元线性回归模型及其R检验结果如下所示:
P1:
(
)
P2:
(
)
P3:
(
)
P4:
(
)
由各断面的多元线性回归模型与R检验结果可知,P1、P2断面的R值均大于0.5,说明这两个多元线性回归模型中的因变量和自变量之间的相关性较好,模型能够较好地描述DO与WT、pH之间的线性关系;P3、P4断面的R值小于0.5,说明这两个模型因变量与自变量之间的线性关系较差,模型对这两个断面DO变化过程的模拟精度较低,其原因是P3、P4断面的DO受沿河工业生活污水排放的影响较大,因此仅考虑WT、pH两个因子的影响时,因变量与自变量的相关性较差;根据P1、P2断面的多元线性回归模型,WT与pH的系数均为负数,说明DO与WT、pH均呈负相关,且pH系数的绝对值均大于WT,说明在变化幅度相同的情况下pH对DO的影响大于WT;P1断面WT与pH的系数的绝对值均大于P2断面,说明P1断面DO与WT、pH的相关性高于P2断面。
3.5.
运移过程模拟结果
利用污染物剪切分散模型模拟P1、P2断面
浓度变化过程,选取每日上午10时(与观测时间相同)的模拟值与实测值进行比较,结果如图10所示。
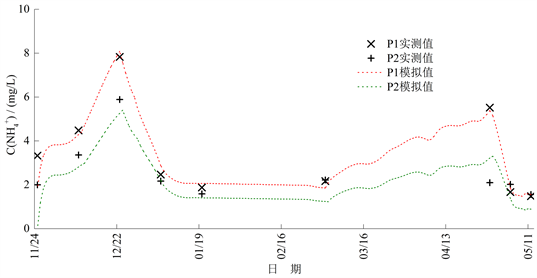
Figure 10. The simulated and measured value of concentration of
in P1 and P2 sections (2018/11/25-2019/5/12)
图10. P1,P2断面
模拟值与实测值(2018/11/25~2019/5/12)
由图10可知,2018年11月至2019年1月P1、P2断面
浓度模拟值与实测值较为接近,模拟精度较高;而2019年3月至5月P2断面模拟值与实测值之间差异较大,其原因是氨氮的降解系数K受WT、水文过程(流速、水深等)的影响 [20],2018年11月至2019年1月WT与水力条件变化较小,模拟精度较高,而2019年3、4月份WT有较大幅度的上升,对污染物降解系数K产生较大影响,但模型中的K取常数(0.095),因此2019年3、4月份P2断面
浓度模拟精度较低。
P1断面的纳什效率系数NSE为0.926,P2断面NSE为0.527。P1断面的模拟精度较高,非常接近实测结果,P2断面的模拟精度低于P1断面;大部分时刻P1断面的相对误差均小于10%;2018年12月至2019年1月P2断面相对误差小于20%,模拟精度较高,而2019年3月至5月相对误差均高于30%,最高达到53.5%,其原因是2019年3月至5月WT与河段的流速、水深等水力条件有较大变化,对污染物降解速率产生较大影响,且由于支流排水对P2断面
浓度的影响,导致P2断面模拟精度下降。
单日
浓度模拟值的变化过程如图11所示(以2018年12月9日与2018年12月23日为例):
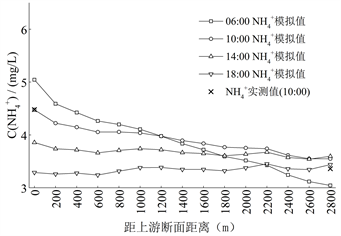 (a)
(a)  (b)
(b)
Figure 11. The simulation results of the distribution of
concentration at different times within one day
图11. 单日内不同时刻
浓度分布的模拟结果
如图11所示,单日内6:00与10:00各断面
浓度从上游到下游依次减小;从6:00至18:00上游断面的
浓度逐渐减小,下游断面逐渐增大,各断面的
浓度逐渐趋近于同一水平,其原因是该模型中污染物降解量只受降解系数K与断面污染物浓度影响,河段上游
浓度高,降解量大,河段下游
浓度较低,降解量较小,使得各断面
浓度最终趋近于同一水平。
综上所述,该模型对研究河段P1断面
浓度变化过程模拟的NSE为0.926,模拟精度高;P2断面的NSE为0.527,模拟精度低于P1断面。2018年11月至2019年1月P2断面的模拟精度较高,但之后的时段由于模型未考虑WT与水力要素(流速等)变化对降解系数K的影响,模拟精度有所降低。总体而言,模型对研究河段
运移过程的模拟精度较高,能够较好地反映河段
浓度的变化过程。
4. 结论
本研究基于扬州城区古运河三湾风景区河段2018年10月至2019年4月常规水质参数与污染物离子浓度的观测数据,采用变异系数法、单因子水质标识指数法与多元线性回归法对水质参数进行分析,并构建污染物随流分散模型对研究河段
运移过程进行数值模拟,得出主要结论如下:
1) 研究期间WT表现为季节性变化;2019年5月之前研究河段的pH与EC呈上升趋势,之后pH与EC呈下降趋势;大部分时段支流的DO低于干流,EC高于干流。
2) 研究期间各断面常规水质参数的总变异系数与权重从大到小依次为DO > WT > EC > pH;各断面的EC和pH的逐月变异系数基本小于0.1,波动程度较小;大部分时段内P3、P4断面同期的EC、DO、pH的逐月变异系数大于P1、P2。
3) 2018年10月至11月P1、P2断面水质类别多为Ⅲ类水;2018年12月至2019年1月P2断面受支流排水影响导致Pi升高,水质多为Ⅳ、Ⅴ类水;P3、P4断面除2018年10月,其余时段水质类别多为IV、V甚至劣V类水;支流受沿河工业生活污水随机排放影响,pH与Pi变化的随机性较强。
4) 根据P1、P2断面的多元线性回归模型,DO随WT、pH升高而减小,且pH的变化对DO的影响大于WT;P3、P4断面水质由于受沿河工业生活污水随机排放影响较大,因此仅考虑WT和pH这两个因子的多元线性回归模型不能较好地反映三者之间的线性关系。
5)
随流分散模型对研究河段2018年11月至2019年1月的
模拟精度较高,之后时段由于未考虑WT对降解系数K的影响,P2断面的模拟精度较低;单日内河段上游
浓度逐渐降低,河段下游
浓度逐渐增大,各断面
浓度逐渐趋于同一水平。
基金项目
国家自然科学基金项目(41271046),2018年扬州大学青蓝工程项目,2019年度扬州市科协软科学项目(2019059),2019年度扬州大运河研究院开放课题。
NOTES
*通讯作者。