1. 引言
半参数部分线性变系数模型是近几十年来发展起来的一种统计模型,既含有线性模型部分,又含有变系数模型部分,是线性模型与变系数模型的结合,因此其具有线性模型便于解释和非参数模型稳健的特征。部分线性变系数模型的形式如下:
(1.1)
其中Y是响应变量,X,Z和T为协变量,为了避免“维数祸根”,我们一般假设T为单变量,
是
维的未知参数向量,
是
维未知的系数函数向量,
为模型误差并且满足
,
。这个模型是一般的且包含许多重要
的统计模型,比如:当
,其中
是一个常数向量时,模型(1.1)就变成通常的线性回归模型,这个模型被用到实际生活的许多方面,现在已经研究的非常成熟;当
且
时,模型(1.1)就变成了部分线性回归模型,这个模型也用的相当广泛,Engle等 [1] 用此模型研究了气温与用电量关系之后,部分线性模型受到了统计学家的重点关注,在理论和应用中都得到了更深入的研究,并取得了一系列突破性成果;当
时,模型(1.1)就变成著名的变系数模型,由于其良好的解释能力,变系数模型得到了广泛的应用,被成功应用到非线性时间序列建模、函数型数据和纵向数据分析、空间分析以及金融计量分析等相关问题的研究中。针对此模型,Fan和Huang [2] 对参数分量提出了Profile最小二乘估计,并且基于广义似然比检验方法研究了该模型参数和非参数函数的假设检验问题;Huang和Zhang [3] 则利用经验似然方法研究了非参数分量
的统计推断问题。
在实际问题分析中经常会遇到数据缺失的现象。因此,在数据缺失下的研究是非常有必要的。随机缺失(MAR)的基本思想是观测到响应变量的概率仅仅依赖于其他观测变量的值,而不依赖于那些缺失值。例如,假设得到来自
的一个不完全观测样本
(1.2)
其中
为可完全观测到的协变量,
为响应变量且带有随机缺失(MAR),
为指示变量。即,如果
,则表示
缺失;如果
,则表示
不缺失。随机缺失机制意味着给定X的条件下Y和
是相对独立的,即
(1.3)
随机缺失是在分析缺失数据时的一种常用假设,这在许多实际情况下是较为合理的。针对缺失数据的研究和处理一直被统计学家所重视,对模型(1.1),Wei [4] 研究了在因变量随机缺失情形下参数的统计推断问题以及基于广义似然比检验方法研究了该模型参数的假设检验问题;Wei和Mei [5] 是基于广义似然比检验对参数部分X带测量误差和因变量Y随机缺失下考虑了参数的估计问题。
在许多实际应用中,我们往往无法得到协变量的精确值,只能采集到含有误差的观测值,比如在工程计算、经济学、生物医学和流行病学等领域,由于实验仪器的原因采集到的数据经常含有测量误差。在模型(1.1)中,非参数协变量Z是可精确观测的,我们所考虑的问题是
含有测量误差,即我们所观测到的是
而不是
,两者之间的关系满足
(1.4)
其中
是测量误差,且独立于
,其协方差阵为
。为了模型的可识别性,我们假设
是已知的,如果该协方差未知,则可以利用W的重复观测数据得到
的估计值。对于上述情况,Yang等 [6] 研究了带测量误差的部分线性模型参数的两步估计以及参数的经验似然置信域;针对模型(1.1),You和Chen [7] 研究了当协变量X含误差时参数的估计问题;Zhang和li等 [8] 研究了在约束条件下协变量X含误差时参数的统计推断问题;Fan和Liang等 [9] 基于经验似然方法研究了当自变量X含误差时参数的估计问题,构造了参数的经验似然置信域;Feng和Xue等 [10] 研究了在约束条件下协变量Z含误差时的参数的估计和假设检验问题;Fan和Xu等 [11] 考虑了协变量Z含误差时基于带辅助信息的经验似然的参数和非参数函数的估计问题,并证明了估计的渐近性质。本文则针对模型(1.1)同时考虑响应变量随机缺失和非参数部分带测量误差。
2. 模型与参数估计
我们首先基于完整数据给出模型(1.1)中系数函数
的估计,假设
为来自模型(1.1)的观测数据,则有
(2.1)
假定
已知,则模型变为如下形式的变系数模型
(2.2)
利用局部线性光滑的局部最小二乘法来估计未知系数函数。给定T领域内的一点t,对
利用Taylor展开有
(2.3)
其中
为
的一阶导数,对
,
极小化
(2.4)
其中
,
为核函数,h为带宽。为了表示方便,引入下面记号
,
,
,
,
,
,
,
,
则式(2.4)的解为
(2.5)
上面在估计时假定了数据Z可以精确观测。如果我们简单的用W来代替Z,而没有考虑测量误差的情况,可以证明这样得到的估计是不相合的,为了解决这个问题,我们需要对估计进行“校正衰减”,纠偏之后的估计为
(2.6)
其中
和
有相同的形式,仅仅用
替代
,并且
其中
为Kronecker乘积。因此当
已知时,纠偏后的系数函数
的估计为
(2.7)
其中
为q阶单位阵,
是
的0矩阵。令
。
,
,
,
,通过极小化下式
(2.8)
可以得到参数
的估计
(2.9)
参数
估计的矩阵形式为
其中
。
再由(2.7)式,我们可以得到系数函数
的估计为
(2.10)
3. 经验似然推断
下面我们给出模型(1.1)回归参数的经验似然比,由(2.9)式可知,
是下面方程的解
(3.1)
由此我们引进辅助随机变量
(3.2)
通过Qin和Lawless [12],基于经验似然方法,关于
的经验对数似然比函数可以定义为
(3.3)
使用Lagrange乘子法可以算出
(3.4)
其中
是下面方程的解
(3.5)
由上可知,经验对数似然比可以表示为
(3.6)
4. 模拟研究
本节通过数值模拟来研究所提方法的有限样本性质。考虑如下的部分线性变系数含误差模型
其中
,
,
,
,
,
,
,
,
分别取
和
两种情况。为了研究模型误差对结果的影响,我们设定误差
有以下形式:
。模拟中我们选取Epanechnikov核函数,即
。并采用“去一个体”交叉验证的方法来选择带宽
,使其满足下列式子达到最小
其中
和
分别为去掉第i个观测值后的
和
的估计。分别考虑如下两种形式的缺失机制:
Case I
,对所有的
;
Case II
,当
时,否则取0.88。
下面我们分别给出不带缺失数据和非参数分量含测量误差不纠偏的
的估计公式,以便于与本文得出的结果作对比。
1) 不含缺失数据:
上述两个公式可以在Feng和Xue [10] 这篇文章中找到。
2) 非参数分量含测量误差不纠偏:
上述两个公式可以在 [13] 中找到相似的结果。
在上述两种缺失情形下,数据Y的平均缺失概率为别为0.2和0.1。在模拟过程中,对于每种情况,样本容量分别取
,并进行1000次模拟,得到了
和
的均值、标准差和均方误差,结果如表1、表2、表3所示。在样本量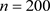 及响应变量Y的平均缺失概率为0.2和
的情形下,我们在图1中给出了模型中非参数函数的估计曲线。此外,在给定两种不同的缺失水平下,分别用经验似然方法(EL)和正态逼近方法(NA)给出参数
的置信水平为95%的置信区间,并计算出置信区间的平均长度及覆盖概率,结果如表4所示。
及响应变量Y的平均缺失概率为0.2和
的情形下,我们在图1中给出了模型中非参数函数的估计曲线。此外,在给定两种不同的缺失水平下,分别用经验似然方法(EL)和正态逼近方法(NA)给出参数
的置信水平为95%的置信区间,并计算出置信区间的平均长度及覆盖概率,结果如表4所示。

Table 1. Mean, SD and MSE of β ^ under different conditions
表1. 不同情况下
的均值(Mean)、标准差(SD)和均方误差(MSE)

Table 2. Mean, SD and MSE of β ¯ under different conditions
表2. 不同情况下
的均值(Mean)、标准差(SD)和均方误差(MSE)

Table 3. Mean, SD and MSE of β ˜ under different conditions
表3. 不同情况下
的均值(Mean)、标准差(SD)和均方误差(MSE)

Table 4. Average length and coverage probability of β confidence interval for 95% confidence level under different conditions
表4. 不同情形下置信水平为95%的
的置信区间的平均长度和覆盖概率
从表1中我们可以得到三个结论:
1) 在缺失概率和测量误差协方差给定的情况下,随着样本的增加,参数估计量的标准差和均方误差都逐渐减小;
2) 在缺失概率和样本量给定的情况下,测量误差协方差越小,参数估计量的标准差和均方误差越小;
3) 在测量误差协方差和样本量给定的情况下,缺失概率越小,参数估计量的标准差和均方误差越小。
通过对表1与表2对比可以得知:
本文所用的处理缺失数据的方法与无缺失数据的结果相差不大,很好地说明了本文所论述方法的优良性。
通过对表1与表3对比可以得知:
1) 在对含测量误差不做任何处理时,得到的结果偏差较大,不能使人满意。
2) 本文所提的方法对含有测量误差数据的处理有很好的效果。
从表4中我们可以得到如下四个结论:
1) EL (经验似然法)比NA (正态近似法)有更短的置信区间和更高的覆盖率;
2) 对给定的缺失概率,随着样本量的增加,经验似然和正态近似的置信区间均会缩短;
3) 对给定的样本量,随着缺失概率的增加,经验似然和正态近似的置信区间均会增长;
4) 对给定的样本量和缺失概率,误差方差越大,不论是经验似然还是正态近似的置信区间均会增长,且覆盖率会下降。
从图1可以看出我们所提出的非参数函数的估计量(虚线)与无缺失数据(点虚线)情形下是几乎重合的,非常接近于真实(实线)曲线,而不纠偏时估计(点线)的效果显然是较差的,这表明我们所提出的非参数部分的估计量是有效的。
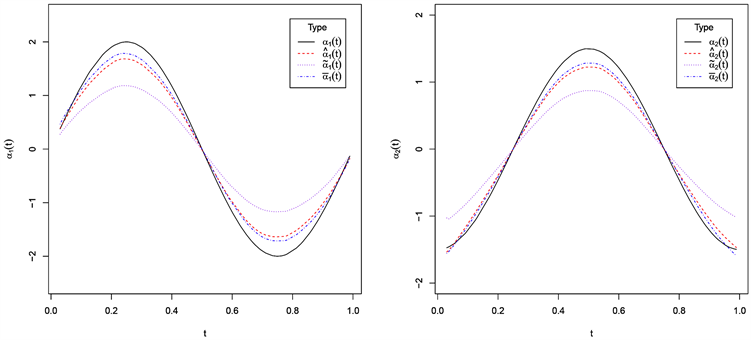
Figure 1. Real curve and all kinds of estimation curves of coefficient function (The left picture is
, right picture is
图1. 系数函数(左图为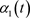 ,右图为
)的真实曲线和各类估计曲线
,右图为
)的真实曲线和各类估计曲线
5. 实例分析
下面通过分析超市生鲜产品销售量的数据进一步说明我们方法的有效性。数据源于日本某公司分析客流量、天气、产品价格等因素对超市生鲜产品销售量影响的工作。该数据集由生鲜产品销售量和客流量、生鲜产品价格、天气情况、是否是节假日一些变量构成,其中生鲜产品销售量为2017年11月至2019年7月店铺中生鲜产品每天的销售量(包含打折数量),九个感兴趣的协变量分别为:生鲜产品价格(PFP)、客流量(VOC)、恶劣天气程度(SWC)、平均气温(MT)、最高气温(MaxT)、平均湿度(MH)、平均降雨(MR)、最大风力(MWF)、是否是节假日(HD)。为了符号简单起见,协变量PFP,MT,MaxT,MH,MR,MWF,VOC,HD分别记为
。
取
为截距项,协变量
。研究讨论了
以及SWC对超市生鲜产品销售量的影响,并采用部分线性变系数模型
来拟合给定的数据。在进行分析之前,我们首先对协变量进行标准化变换,同时需要对变量SWC进行变换使其分布为
。为了证明我们所提方法的有效性,我们假定
带有测量误差,即
其中
,响应变量有5%的缺失值,模拟中
的产生是随机的,选取Epanechnikov核函数,即
,通过“去一个体”交叉验证的方法来选择带宽
,通过本章提出的方
法所得参数分量
的估计
的值为2.9711,置信区间为[2.7546, 3.1876];
的估计
的值为3.3058,置信区间为[−3.0865, −3.5251]。协变量客流量
和是否是节假日
的系数估计值
和
分别为2.9711和3.3058,说明随着客流量的增加或当天为节假日时,生鲜产品的销售量也是递增的,销售量与协变量之间有正相关关系。这也与实际情况相符合。
NOTES
*通讯作者。