1. 时间不一致问题及其数学模型
在本节主要阐述时间不一致问题的内涵及其数学模型。为此,我们首先借助一个例子来说明时间一致的内涵。考虑没有通货膨胀情形下的银行存款问题。让
表示初始存款,r表示年利率。在复利的意义下,在第t年年底的收益为
。进而,对任意给定的未来时间
,显然对
有
。这意味着
这表明:无论我们是在
时刻还是
时刻将钱存入银行,最终收益均相同。此问题本质是一个决策问题,表明我们的决策不受时间因素的影响。
事实上,在不同时空背景下,即使是同一个人决策心态也是完全不一样的。为此我们借用1988年诺贝尔经济学奖得主Maurice Allais在1953年的所做一个实验 [1],但为了叙述简明和通俗易懂,容许我们对数字作微小修改。对第一组实验:A、你有10%的机会赢1000万英镑,90%的机会分文不会赢;B、你一定赢100万英镑,Allais实验表明绝大多数人会选择B。但对第二组实验:A、你有10%的机会输1000万英镑,90%的机会分文不会输;B、你一定输100万英镑,Allais实验表明绝大多数人会选择A。如果我们按照通常的观点将人划分为保守型和风险型两类,一个自然有趣的问题是你自己是属于保守型还是风险性呢?这就是著名Allais悖论。
对比上述的银行存款问题和Allais悖论,我们给出时间不一致问题的定义。对于一个涉及决策的问题,如果在t时刻作出的最优决策,在任意时刻
来看此决策都是最优的,我们称这类问题是时间一致问题,否则称为时间不一致问题。这个定义最早是雍炯敏教授给出的。显而易见,假设决策者是理性的,如果问题是时间一致的,一旦我们做出最优决策,我们将永远不会后悔。如果整个世界是时间一致的,则事情将变得非常理想,生活也将变得轻松自在。但是,如果真是这样的话,我们的生活将可能变得有点无聊。幸运的是,生活并不是那么理想!因为,时间不一致问题几乎无处不在!例如著名的双曲贴现就是典型的时间不一致问题 [2]。又如2002诺贝尔奖得主Kahneman [3] 在1979年提出的前景理论(Prospect Theory)就是描述和预测人们在面临风险决策过程中表现与传统期望值理论和期望效用理论不一致的行为理论。他发现人们在面对得失时的风险偏好行为不一致,在面对“失”时变得风险追求,而面对“得”时却表现得风险规避。这表明参照点的设立和变化会影响人们的得失感受,并进而影响人们的决策。从数学角度看,我们认为引起时间不一致的根本原因有三方面:一是非指数贴现;二是非线性条件期望;三是记忆效应。
在本节结束之前,我们陈述时间不一致问题的数学模型。控制集(或策略集)表示为
受控系统为
问题就是极小化或极大化下列目标泛函
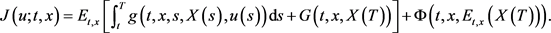
值得注意的是,在目标泛函中,期望及其函数
均依赖于初始状态
,这恰好是时间一致问题所不容许的。一言以蔽之,当期望及其函数
均不依赖于初始状态
时,问题是时间一致的,否则就是时间不一致的。
2. 时间不一致问题的发展历程
关于时间不一致问题的定性分析,至少可以追溯到1739年Hume [4] 和1759年Smith [5] 的工作。至此以后,越来越多的学者关注此问题。尽管如此,直到1955年,Strotz [6] 才首次对时间不一致问题进行公式化,不仅拓宽研究了视角,更为重要的是为数学施展手脚提供了新的场域。从数学角度看,自1955年到2010年,这段时间主要研究离散动力系统、简单的常微分方程和随机常微分方程支配的非指数贴现问题,如著名数学家Ekeland [7] [8] [9] 以及Basak、Chabakauri、Bjork、Murgoci等人的工作,获得一些有意义的成果。当然,也有不少学者从实证研究的角度考虑了时间不一致问题,诸如诺贝尔奖得主Edward C. Prescott教授和Richard Thaler教授等。这个领域主要是一些著名的行为经济学者开展了相关研究,成果也十分丰富。著名数学家雍炯敏教授也长期致力于时间不一致问题的研究。特别地,雍教授在2014年首尔召开的国际数学家大会上作了《时间不一致问题》的专题报告 [10],自此时间不一致问题成为数学与金融、经济的交叉前沿课题。
关于时间不一致问题的研究,主要包括实证研究(如2004年诺贝尔经济学家Edward C.Prescott的经济政策时间一致性理论 [11] 、2017年诺贝尔经济学家Richard Thaler的获奖工作的禀赋理论 [12] 等)和理论研究两个方面。特别是在理论研究方面,依据对时间不一致问题解的定义,主要包括三个方面,一是雍炯敏教授在2012年引进的时间一致均衡控制,二是周迅宇教授等人2013年引进的开环均衡控制,三是经济学家期望的闭环均衡控制。到目前为止,以雍炯敏教授为首的相关学者关于时间不一致问题的时间一致均衡控制的理论成果最为丰富,同时他们也研究了开环均衡控制。对时间不一致的闭环均衡控制的研究很长一段时间未取得进展,但近期彭云飞教授及其带领学生通过研究积微分Riccati方程组,建立了一类时间不一致LQ问题的闭环均衡控制的基本理论。同时,彭云飞与著名行为经济学家周迅宇教授合作,开展了一般时间不一致控制问题闭环均衡控制的研究,近期也取得了进展。
这里需要特别指出的是,雍炯敏教授也研究了闭环均衡控制(或称时间一致闭环均衡控制),但与经济学家期望的闭环均衡控制是有区别的。
3. 时间一致均衡控制
雍炯敏教授从非合作微分博弈的思想研究时间不一致问题,自2012年引进时间一致均衡控制以来并建立了一套理论。
雍教授在文章 [13] 中考虑了如下问题:控制集为
,受控系统为
问题是极小化下列目标泛函
为此,对时间区间
,引进分割
以及联系
的N人微分博弈,第k位玩家从
中选取控制。对任意的
定义控制
为
为了叙述方便,在不引起混淆的情况下,让
。对给定
,
下列方程的解
第k个玩家的支付函数定义如下
问题
寻找控制
得对每个
,
若上述问题
存在,则
为问题
的均衡控制。而关于问题
:对任意的
,寻找控制使
得对任意
,存在
,当区间
的任意分割
适合
有
(1)
如果控制
满足上述条件,则将之称为问题
的时间一致均衡控制。进而,在此基础上讨论了时间一致均衡控制的存在性。这个解法的核心思想是将时间不一致问题视为时间一致问题的极限。
雍炯敏教授在文章 [14] 中运用相同的思想,引进时间一致闭环均衡控制。受控系统为
目标泛函为
为了凸出思想和叙述简明,我们以对应的确定型的问题来陈述。引进问题(N)对任意给定初始对
寻找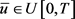 满足
满足

一个连续映射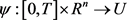 称为问题(N)的时间一致均衡控制,如果对任意
称为问题(N)的时间一致均衡控制,如果对任意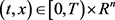 ,下列微分方程
,下列微分方程

存在唯一解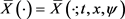 且对任意
且对任意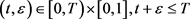 有
有
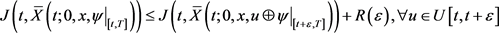
其中
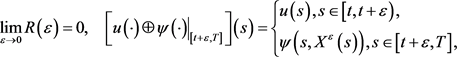
这里的 是下列方程的解
是下列方程的解

他也引进相应的均衡值函数函,建立均衡HJB方程,进而构造了时间一致均衡控制。
雍教授在2017年研究MF-SDE [15] 的控制问题时,引进了一类时间一致闭环控制,进而获得了此问题解的存在性。同样地,为了凸出思想和叙述简明,我们仅叙述对应的确定型的情形。受控系统为
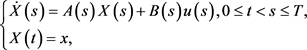
性能指标为
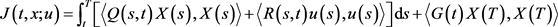
对区间 引进分割
引进分割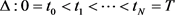 以及联系
以及联系 的
的 是某个映射,称
是某个映射,称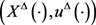 是一闭环对,如果
是一闭环对,如果

且对任意固定的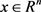 ,
,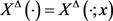 线性方程
线性方程

的解;对任意的 和任意的
和任意的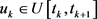 ,
,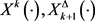 分别是下列方程
分别是下列方程
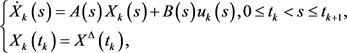
和
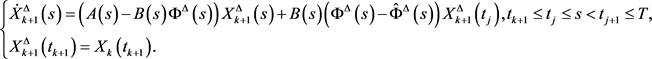
的解,引入记号
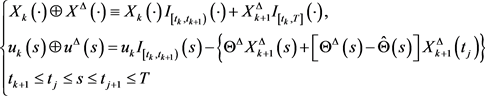
我们称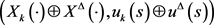 是
是 在
在 上的变分,如果成立
上的变分,如果成立
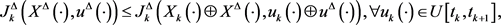
称 是闭环
是闭环 均衡策略,
均衡策略,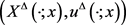 是给定初始状态x的闭环
是给定初始状态x的闭环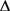 均衡对。
均衡对。
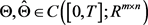 被称为闭环均衡策略,如果满足条件
被称为闭环均衡策略,如果满足条件

对任意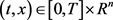 ,让
,让 是下列方程
是下列方程
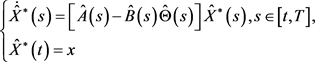
的解。进而定义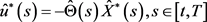 则分别称
则分别称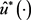 为闭环均衡控制。在此定义的基础上,雍教授讨论闭环均衡控制的存在性。
为闭环均衡控制。在此定义的基础上,雍教授讨论闭环均衡控制的存在性。
4. 开环均衡控制
周迅宇教授在2013年的文章 [16] 引进了开环均衡控制。同样的,为了简明,我们给出对应的有限维确定的情形,即控制系统为
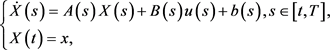
目标泛函为

给定控制 ,
,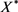 为对应的状态轨线。我们称
为对应的状态轨线。我们称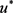 为开环均衡控制,如果满足
为开环均衡控制,如果满足
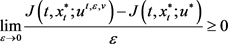 (2)
(2)
其中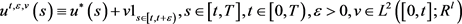 在此基础上,周迅宇等人获得了开环均衡控制存在的充分条件,他们进一步在文章 [17] 中讨论了开环均衡控制的唯一性。此外,雍炯敏教授在文章 [15] 中也考虑了在次意义下开环均衡控制。
在此基础上,周迅宇等人获得了开环均衡控制存在的充分条件,他们进一步在文章 [17] 中讨论了开环均衡控制的唯一性。此外,雍炯敏教授在文章 [15] 中也考虑了在次意义下开环均衡控制。
此外,彭云飞教授等人也讨论了一般常微分方程支配的时间不一致控制问题开环均衡控制的存在性。
5. 闭环均衡控制
时间不一致问题是数学与金融交叉的前沿课题,长期以来许多知名经济学家都十分关注该问题的求解。经济学家给出了时间不一致问题的闭环均衡控制的定义:函数 称闭环均衡控制,如果对任意的
称闭环均衡控制,如果对任意的 和对任意的
和对任意的 成立
成立
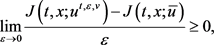 (3)
(3)
其中
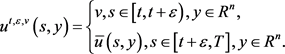
他们认为这样的解才能刻画实际问题。很显然,这与前面的(1)和(2)有本质区别。
但长期以来闭环均衡控制的存在性一直是未知的。Bjork等人在文章 [18] 中研究了一类系统为马尔科夫过程的时间不一致问题。他假设闭环均衡控制存在,定义了均衡值函数,和均衡值函数所满足的一个偏微分方程,他称之为拓展HJB方程。进一步,他证明了一个验证性定理:如果拓展HJB方程有解,则闭环均衡控制存在。
2014年周迅宇教授与彭云飞教授获得了刻画值函数的均衡原理,并由此导出了Bjork所得到的拓展HJB方程。2018年彭云飞教授等人证明了一类常微分方程系统支配的时间不一致问题闭环均衡控制的存在性 [19]。与此同时,他们也考虑了一类时间不一致LQ问题:其中控制集为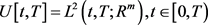 ,受控系统为
,受控系统为
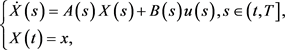
目标泛函为
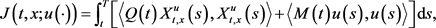
其中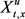 是系统在给定初始状态
是系统在给定初始状态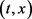 及控制u时所对应的解。彭云飞教授不仅获得(3)的意义下的闭环均衡控制的存在性,进一步还引进一类两点边值问题和一类耦合Riccati方程,讨论了上述时间不一致问题均衡控制的存在性等价于两点边值问题解的存在性,也等价于Riccati方程解的存在性。
及控制u时所对应的解。彭云飞教授不仅获得(3)的意义下的闭环均衡控制的存在性,进一步还引进一类两点边值问题和一类耦合Riccati方程,讨论了上述时间不一致问题均衡控制的存在性等价于两点边值问题解的存在性,也等价于Riccati方程解的存在性。
6. 展望
时间不一致问题历史悠久,运用广泛,目前已经取得许多进展。但依旧有许多问题亟待解决,如一般常微分方程系统支配的时间不一致问题,时间不一致控制的一般理论,无限时区上时间不一致LQ问题等诸多问题仍需有待进一步研究。
基金项目
本文获得国家自然科学基金项目(11661020)资助。