1. 引言
本文主要用于研究如下非线性无约束最优化问题
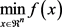 (1.1)
(1.1)
其中
是连续可微函数。本文的方法是通过更新迭代式
(1.2)
来解决问题(1.1),
是搜索方向,
是步长。
牛顿法是解无约束优化最经典也是最早的算法之一,作为最基本的求解无约束优化问题的方法,牛顿法及其各种改进方法一直受到广泛关注(见文献 [1] [2] [3] [4])。下面是牛顿法的原理:
假设
是当前迭代点,计算
处目标函数的梯度 和Hessian矩阵
。若
和Hessian矩阵
。若  ,则根据目标函数的二次可微性知,目标函数在
,则根据目标函数的二次可微性知,目标函数在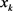 附近是严格凸函数。基于目标函数的二次泰勒展式,在当前迭代点
附近:
附近是严格凸函数。基于目标函数的二次泰勒展式,在当前迭代点
附近:
(1.3)
所以,考虑
(1.4)
假定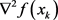 是正定的,则知该式的解是
是正定的,则知该式的解是
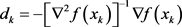 (1.5)
(1.5)
上式就是牛顿搜索方向。牛顿方向 被附加到(1.2)的搜索方向而不是直接替代主要基于以下几个考虑:首先(1.1)对于 [5] 中的问题,函数
的Hess矩阵可能不正定,即使我们假设f在
上连续可微,也可能初始点的选取没有足够靠近“极小点”,牛顿法的一些理想性质不在初始点附近,其次通过结合谱梯度法,能够避免求得的(1.1)式的解被困在局部最小值中。
被附加到(1.2)的搜索方向而不是直接替代主要基于以下几个考虑:首先(1.1)对于 [5] 中的问题,函数
的Hess矩阵可能不正定,即使我们假设f在
上连续可微,也可能初始点的选取没有足够靠近“极小点”,牛顿法的一些理想性质不在初始点附近,其次通过结合谱梯度法,能够避免求得的(1.1)式的解被困在局部最小值中。
BB步是由Barzilai和Barwein在1988年提出的两点步长梯度法 [6],其基本思想是利用迭代当前点以及前一点的信息来确定步长因子。1993年和2002年Raydan和Dai & Liao证明了广义n维严格凸二次型BB方法的全局收敛性和R-线性收敛性。随后,BB方法也扩展以解决一般的非线性优化问题。通过将Grippo等提出的非单调线搜索 [7] [8] [9] 结合起来,1997年Marcos Raydan在文献 [10] 中提出了一种加入全局策略的GBB算法,2018年Yu-Hong Dai在文章 [11] 中,提出了一族谱梯度法,并证明了此类算法在任意维情况下都具有R阶超线性收敛性。下面是该方法的原理:
他们是把迭代公式
看成是
(1.6)
其中
,
.为了使矩阵
具有“拟牛顿”性质,计算
使得
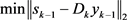 (1.7)
(1.7)
或者
(1.8)
其中
,
,由上两式分别求得
(1.9)
和
(1.10)
上面两式就是谱梯度步长。在一般的非二次情况下, ,
可以是令人无法接受的大或小(甚至对于非凸函数是负的),因此我们必须假设逐步计算出的
是通过对(1.10)或(1.11)进行修改,以满足形式的一个条件
,
可以是令人无法接受的大或小(甚至对于非凸函数是负的),因此我们必须假设逐步计算出的
是通过对(1.10)或(1.11)进行修改,以满足形式的一个条件
(1.11)
若不然,则令
。
现在我们给出一个简短的分析,形成了一个针对问题(1.1)的牛顿谱梯度法。对任意的 当
时,设
当
时,设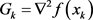 是目标函数的Hessian矩阵。由于目标函数f是连续可微的,所以如果下列方程
是目标函数的Hessian矩阵。由于目标函数f是连续可微的,所以如果下列方程
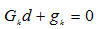 (1.12)
(1.12)
有解 ,则
在
,则
在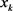 处的方向为下降方向,并称为f在
的牛顿方向。且由论文 [12] 得,序列
的任何极限点
都是f的稳定点,既
。
处的方向为下降方向,并称为f在
的牛顿方向。且由论文 [12] 得,序列
的任何极限点
都是f的稳定点,既
。
谱梯度法因其几乎对所有初始值都是成立的而得到广泛的应用。从而弥补了牛顿法对初始点的苛刻要求,并且该方法不需要求解目标函数f的Hessian矩阵。因此有如下谱梯度方向
(1.13)
在本文中,我们结合(1.6)和(1.12)引入牛顿方向和谱梯度方向的凸组合来最大化利用这两种方法的优势。对于任给的
设
(1.14)
其中谱梯度方向
有一个缺点是该方向不总是下降的。为了克服这一缺点,本文结合Grippo等提出的非单调线搜索,从而避免了谱梯度法不是单调下降的问题。
(1.15)
其中步长
。
文章剩下的部分组织如下:第二节给出了搜索方向的性质并描述了具体的牛顿谱梯度方法;第三节证明了算法的收敛性;第四节给出了数值实验,第五节进行了总结。
2. 搜索方向的性质及牛顿谱梯度法
算法2.1 (牛顿谱梯度算法)
步0 给定初始点
,终止误差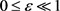 。令 k:=0
。令 k:=0
步1 计算 。若
,停算,输出
作为近似极小点。
。若
,停算,输出
作为近似极小点。
步2 由(1.10)或(1.11)给出满足条件(1.12)的
.
步3 计算
,解方程组
(2.1)
若(2.1)有解
,且满足
,转步3;否则,令
转步5。
步4
.
步5 由非单调线搜索技术确定步长因子 。(
是满足条件的最小非负整数)
。(
是满足条件的最小非负整数)
 (2.2)
(2.2)
步6 令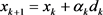 ,
,转步1。
,
,转步1。
首先,我们将研究
的一些性质,且我们假定目标函数f在
上总是二次连续可微的,且满足下列假设1:
假设1 目标函数
二次连续可微,对任意给定
,f在水平集
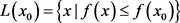 (2.3)
(2.3)
上有界的。
假设2 存在
的一个领域
,使得
在该邻域内Lipschitz连续,既存在一个常数
使得

假设3 存在 的一个领域
,使得
的一个领域
,使得 在该邻域内Lipschitz连续,既存在一个常数
在该邻域内Lipschitz连续,既存在一个常数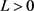 ,使得
,使得
为了证明收敛性定理,首先给出如下性质:下列性质证明该算法的方向是下降方向。
定理2.1 假设
不是(1.1)的稳定点,由式(2.1)计算得到的 存在且
。则存在
存在且
。则存在 使得,
使得,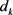 是f在x处的下降方向且满足(2.2)式。
是f在x处的下降方向且满足(2.2)式。
证明:因为f是连续可微的,对于给定的
通过(1.12)和(1.6)有
根据正定矩阵的逆矩阵仍然是正定矩阵的性质,显然有
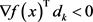 . (2.4)
. (2.4)
对任给的 ,有
,有
 (2.5)
(2.5)
且对任给的k都有
故有
结合(2.4),对任给的 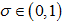 ,(2.2)成立。
,(2.2)成立。
目前为止,我们已经考虑了非稳定点
处的搜索方向 的一些全局性质,为了证明我们算法的超线性收敛性,我们接下来考虑解点周围的方向的性质。
的一些全局性质,为了证明我们算法的超线性收敛性,我们接下来考虑解点周围的方向的性质。
定理2.2 假设
是
的解,存在
一个常数
,对任给的 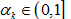 ,
,
且对于
,
,有
证明:详见参考文献 [13] 定理3.2。
3. 收敛性分析
针对我们的牛顿谱梯度法,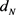 是通过求解线性系统(2.1)得到,如果(2.1)是不可解的或者矩阵
是高度病态的,则
,这意味着
是通过求解线性系统(2.1)得到,如果(2.1)是不可解的或者矩阵
是高度病态的,则
,这意味着 。其次,通过定理2.1,如果
。其次,通过定理2.1,如果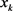 不是(1.1)的稳定点,且算法2.1的步骤5有很好的定义,则我们的算法要么停止在一个稳定点,要么生成一个无穷序列
。
不是(1.1)的稳定点,且算法2.1的步骤5有很好的定义,则我们的算法要么停止在一个稳定点,要么生成一个无穷序列
。
定理3.1 设
是由算法2.1生成的序列,且满足假设1,则下列性质成立:
(a) 序列
的任何极限点 都是f的稳定点,既满足
都是f的稳定点,既满足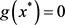 ;
;
(b)
的任何极限点
都不是f的极大值点;
(c) 如果
只有有限个稳定点,则序列
本身收敛。
证明:为了证明性质(a),我们结合定理2.1使用了( [7], p709)中的收敛性证明部分。
我们定义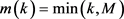 ,显然
,
,显然
, 对所有的
,另外,对任给的k有
,最后存在正数
对所有的
,另外,对任给的k有
,最后存在正数 和
使得搜索方向
和
使得搜索方向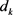 满足
满足
, 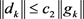
实际上,在牛顿谱梯度法中
,对于所有的
因为
正定,故
正定,即对一切 有
,而
,所以存在一个正数p,使得
有
,而
,所以存在一个正数p,使得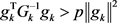 ,从而有
,另外,
,从而有
,另外,
由
的正定性及f二次连续可微可知,存在
的一个领域
,使得对任意的 ,都有
是一致正定的。特别的,
在上有界,既存在常数
,使得
,故而
。
,都有
是一致正定的。特别的,
在上有界,既存在常数
,使得
,故而
。
对任给的
,
,令
, 。
。
因此,根据( [9], p711)中的等式(14),我们得到
因为
,(a)式得证。
(b)和(c)的证明直接由 [9] 中的收敛性定理给出。
定理3.2设函数
二次连续可微,
由算法2.1产生的迭代序列,且满足假设2,设
聚点 是f的解。
是f的解。 正定,则
超线性收敛于f的全局极小点
。
正定,则
超线性收敛于f的全局极小点
。
证明:由
的正定性及f二次连续可微可知,存在
的一个领域
,使得对任意的
,都有
是一致正定的。特别的,
在上有界,既存在常数
,使得
。又由
的连续性知,存在邻域
,使得
因此,当
时,有

从而有
,既
超线性收敛于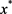 。
。
4. 数值实验
本文从文献 [5] 中取出38个标准测试问题进行数值实验,目的是比较本文算法与几种经典无约束优化算法的数值效果以及对本文不同M值的算法的试验效果。所有数值实验都是在WINDOWS10操作系统,CPU频率为2.0 GHz,内存为2 GB的个人计算机上进行。各参数选取如下: ,
,
,
。其中如果步2中
不满足(1.12),则参数
,
,
,
。其中如果步2中
不满足(1.12),则参数 由下列式子给出:
由下列式子给出:
(4.1)
表1中列出了各计算结果,其中各列的代表含义如下:k:迭代次数;flag:函数值的计算次数;
:算法求得的最优值。文中的初始点
采用文献 [5] 中给定的用来试验函数正确性的点作为初始点;终止条件采用
。
表1选取M = 1,M = 2,M = 5,M = 10对本文算法进行比较,计算出不同的M值函数的迭代次数k,函数值的计算次数flag和函数值
,并进行了比较。凸组合参数t的选取是通过比较t = 0.4, 0.5, 0.55,0.6,0.618这几个参数选取的,通过比较发现当
时,表现效果较佳,因此选择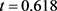 。其次从表中可以看出当M = 10时,该算法在最优函数值,函数值的计算次数以及迭代次数上对更多函数都是好的,因此选用M = 10时的函数计算效果与其他方法进行比较。表2中主要把共轭梯度法,BFGS拟牛顿法同本文中的算法进行比较。
。其次从表中可以看出当M = 10时,该算法在最优函数值,函数值的计算次数以及迭代次数上对更多函数都是好的,因此选用M = 10时的函数计算效果与其他方法进行比较。表2中主要把共轭梯度法,BFGS拟牛顿法同本文中的算法进行比较。


Table 1. Different algorithms with the comparison of this algorithm
表1. 不同算法同本文算法的比较

Table 2. Comparing different M value algorithm
表2. 不同M取值的算法比较
从表2中能明显地看出,本文的算法在很大一部分函数中都有很好的计算效果,在27个函数中,其中对最优函数值表现好的有20个,对迭代次数表现好的有14个,而从函数值的计算次数来看,几乎处处表现良好。因此我们得到了一个相对比较好的算法。
5. 总结
本文通过介绍牛顿法与谱梯度法的凸组合搜索方向提出一种求解无约束优化问题的牛顿–谱梯度法,该算法实现了好的数值实验结果,即使在牛顿方向奇异的情况。我们在数值试验过程中还发现该方法在某些情况下依然会带有牛顿法中无法达到最优点的问题,但是当添加适当的选择条件时可能会取得更好的实验结果。