1. 引言
神经元是生物神经系统的基本组成单位,通过复杂的放电节律,承担着信息编码、传递、解码的重要功能。由于神经元电生理行为的多样性,在大量数据的基础上建立理论模型进行非线性动力学分析的方法更具优越性。1952年,Hodgkin和Huxley通过对乌贼巨轴突进行电压钳实验,提出钠离子学说,继而建立了基于电导的四维非线性Hodgkin-Huxley模型 [1] 来刻画神经元放电的节律模式。在此基础上,FHN模型、ML模型、HR模型等各类与神经电生理学相关的理论模型纷纷被提出,应用于神经科学的研究。1985年,Chay提出了包含混合钠–钙离子通道、钾离子通道的多尺度三维非线性神经元模型,即Chay模型 [2]。相较于H-H模型,Chay模型新增加了钙离子通道的动力学变量,模拟了簇放电活动,通过慢变过程调节快变过程的放电尖峰,达到静息态和反复放电状态之间的转迁,展示了可兴奋细胞丰富的放电节律模式。
相较于峰放电,簇放电携带了大量的生物信息 [3],展现了丰富的非线性动力学行为。簇放电模式种类繁多,源于慢变量和快变量共同引起的静息状态和发放状态之间转迁模式的复杂性。Rinzel等人 [4] 运用快慢动力学分析将簇放电分为方波簇放电、椭圆簇放电、抛物线簇放电等不同类型的簇放电模式。文献 [5] 在此基础上进行了推广,并且增加了第4种簇放电类型。为了更细致地区分各类簇放电模式,Izhikevich [6] 将簇放电模式划分成不同的拓扑类型 [7],不同的簇放电类型和不同的分岔相对应。由于Chay模型丰富的簇放电模式,大量文献集中在放电节律和模式转迁 [8] [9] 等动力学分析领域,如运用动力学进行分岔分析 [10] [11] [12]:通过余维1分岔,得到神经元Chay模型的各种簇放电模式及发放状态的转迁;通过余维2分岔揭示静息状态和发放状态之间的转迁区域。除此之外,文献 [13] [14] 对神经元Chay模型添加噪声,得到随机神经元Chay模型进行节律编码、共振等探究。以上研究都是针对单个神经元Chay模型进行动力学分析,没有涉及到神经元模型间的联系以及复杂神经元实际放电活动的刻画,因此,本文基于螺旋神经节神经元的形态结构,针对房室化神经元Chay模型进行非线性动力学分析以及相关神经计算。
神经元具有丰富的空间形态和电生理特性,为了更好地研究生物信息在神经元各部分的传递、编码,神经元的时空变化多通过房室模型来描述。房室模型用离散的多个神经元房室逼近连续的单个神经元,更好地刻画了神经元的几何形态结构和生物电生理特征。本文以螺旋神经节神经元的空间形态为房室划分标准,构建了两类房室化神经元Chay模型,数值模拟了神经元模型的发放活动和信息编码,进行分岔分析、神经计算等方面的研究:1) 构建两房室神经元Chay模型,运用非线性动力学理论,研究分岔序列、簇发放模式及其转迁等放电节律。2) 构建15房室神经元Chay模型,模拟信息传递过程中的发放活动。揭示了外界刺激位点的搭配规律,髓鞘结构、脱髓鞘等现象。3) 构建131房室神经元Chay模型。研究内源和外源因素(如依赖于电位的K+离子通道电流的最大电导
和外界电流刺激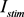 等)以及中枢突的形态结构对于神经冲动产生、传递的影响(包括第一动作电位潜伏期的大小,发放率的高低、最大电位的大小,同步差的大小等)。
等)以及中枢突的形态结构对于神经冲动产生、传递的影响(包括第一动作电位潜伏期的大小,发放率的高低、最大电位的大小,同步差的大小等)。
2. 模型描述
2.1. 神经元Chay模型
1985年,Chay提出了多尺度神经元Chay模型,展示了在静息状态和反复放电状态之间转迁的丰富簇放电模式,其中,不依赖电位而依赖Ca2+离子浓度的K+离子通道是很多可兴奋性细胞的重要特征,因此该模型常用来描述神经元、感觉末梢、心肌细胞等,模型描述如下:
(1)式表示神经元膜电位V的变化速率,右边分别是混合Na+-Ca2+离子通道电流、电导依赖于电位的K+离子通道电流、电导不依赖电位而依赖Ca2+离子浓度的K+离子通道电流和漏电流。(2)式为依赖于电位的K+离子通道打开概率n的变化速率。(3)式则为Ca2+离子浓度C的变化速率。其中,
和
分别是混合Na+-Ca2+离子通道激活和失活概率的稳态值,
、
、
、
分别代表各离子通道的最大电导,
、
、
、
、
为各离子通道的可逆电位,
是n的稳态值, 为弛豫时间,
为弛豫时间,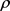 是比例常数,
是细胞内Ca2+离子流出的比率常数。并且
是比例常数,
是细胞内Ca2+离子流出的比率常数。并且
上式中各值分别为:
2.2. 房室模型描述
文献 [15] 中小鼠螺旋神经节神经元的中枢突几何形态结构存在大量中枢突分叉,生物信息经耳蜗核传递至中枢神经系统,本文通过文献 [15] [16] [17] 运用类比的方法重构了完整的小鼠I型螺旋神经节神经元拓扑结构,并基于其形态结构建立了房室化神经元Chay模型。不包裹髓鞘的房室可以进行细胞内外的离子交换,用Chay模型进行描述,如I型螺旋神经节神经元的郎飞结以及II型螺旋神经节神经元。而包裹髓鞘的房室,由于髓鞘的存在,阻碍了细胞内外的离子交换,如I型螺旋神经节神经元的结间节部分,本文用以下式子(此处仅写明主要结构,详细房室连接参照后文)来数值模拟这部分双电缆结构 [18] 房室:
并且,
其中,
是结点膜电容,
是髓鞘膜电容,
是髓鞘层数,
是结间节电导,
是依赖温度的髓鞘膜电阻,
是依赖温度的轴浆膜电阻 [19]。本文对以下各房室模型进行数值求解,所得结果已经过反复验证。
3. 两房室神经元Chay模型
基于重构的螺旋神经节神经元的形态结构,单个神经元房室用Chay模型进行描述,得到两房室神经元Chay模型:
(4)
(5)
(6)
(7)
(8)
(9)
其中,房室1受外加直流电刺激,用式(4)、(5)、(8)表示,房室2用式(6)、(7)、(9)表示,由于Chay模型的电生理参数取值较大,此处添加连接因子k调节房室间连接强度。
3.1. 参数的敏感性
数值模拟发现,两房室神经元Chay模型对于
等内源参数具有很强的敏感性,参数改变对于模型的放电模式、各房室间同步性等节律编码都会造成不同程度的影响。以钙离子通道的可逆电位
为例,通过研究内源参数
对两房室神经元Chay模型的影响,探索模型的不同放电模式。
本文中,如果簇发放的峰峰间距(ISI)为几个固定值,并且簇簇间距(IBI)始终保持不变,即判定膜电位的发放是周期性的簇发放。
3.1.1. 峰峰间距和簇簇间距
从图1(左)可以看到,随着内源参数
的递减,房室1和房室2的ISI序列出现加周期分岔现象,直至
时,出现复杂放电的混沌状态;图1(右)中,与左图相对应,随着
的减小,除了在
等分岔点处以及
的混沌情况下,簇簇间距(IBI)始终保持一固定值不变,即簇与簇之间的时间间隔始终维持恒定。由前述可知,除了在
等分岔点处,以及
所产生的混沌状态下,随着
的减小,房室1和房室2从周期1放电转变为周期性的簇放电,从周期1、2逐次递增直至出现混沌现象,展现了丰富的放电模式及其转化所出现的分岔现象。
3.1.2. 峰相位差和簇相位差
为了研究各房室之间放电模式的同步状态,本文引入峰相位差 [20]:
其中,
分别是两个房室峰值对应的时刻。定义:当
时,两房室是同相峰同步的;当
是几个不等于0和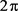 的固定值时,两房室是反相峰同步的;当
在
内任意取值时,两房室是峰异步的。其中,
即
。
的固定值时,两房室是反相峰同步的;当
在
内任意取值时,两房室是峰异步的。其中,
即
。
同理,为了研究各房室之间簇和簇的同步状态,比较簇同步和峰同步之间的区别,本文引入簇相位差 [20],定义如下:
其中,
分别是两房室的每个簇中第一个峰值对应的时刻。定义:当
时,两房室是同相簇同步的;当
是几个不等于0和
的固定值时,两房室是反相簇同步的。当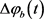 在
内任意取值时,两房室是簇异步的。其中,
即
。
在
内任意取值时,两房室是簇异步的。其中,
即
。
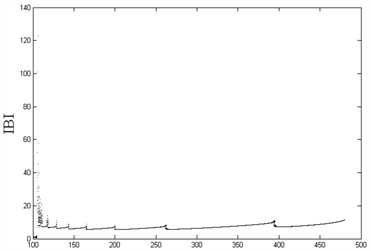
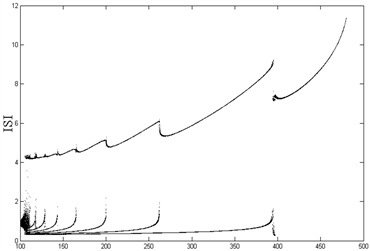
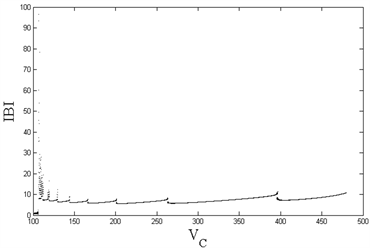
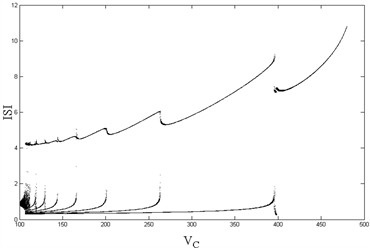
Figure 1. (Top left): Changes in ISI of compartment 1 with VC; (Top right): Changes in IBI of compartment 1 with VC; (Bottom left): Changes in ISI of compartment 2 with VC; (Bottom right): Changes in IBI of compartment 2 with VC
图1. (左上):房室1的ISI随VC的变化;(右上):房室1的IBI随VC的变化;(左下):房室2的ISI随VC的变化;(右下):房室2的IBI随VC的变化
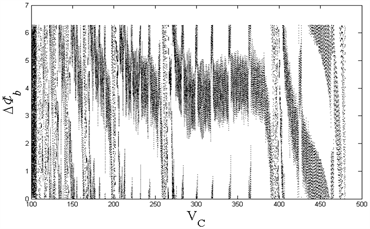
Figure 2. (Left): Phase difference of spikes between compartment 1 and compartment 2; (Right): Phase difference of bursts between compartment 1 and compartment 2
图2. (左):房室1和房室2的峰相位差;(右):房室1和房室2的簇相位差
由图2可知,随着
的递增,房室1和房室2的峰相位差和簇相位差虽然逐渐呈现周期性的规律分布,但是整体上较难达到同相同步的放电模式。基本呈现异步状态;在参数变化范围内取值时,两房室间簇相位差的数目基本不会超过峰相位差的数目,因此图2(左)的分布较图2(右)更为复杂凌乱。通过电生理参数
的调节,得到了两房室间峰同步和簇同步的变化规律,有利于了解整个神经元模型各房室间信息传递的基本节律特性。
3.2. 不同类型的簇放电模式及其转迁
为了进一步分析两房室神经元Chay模型的动力学行为以及复杂簇发放模式的多种类型,本文引入快慢动力学分岔理论 [21] 进行非线性动力学分析。由于式(8)~(9)的参数
一般取值很小,所以与其相关的Ca2+离子浓度的变化速率相较于其它变量的变化速率要小得多。因此,系统(4)~(7)构成快子系统,其中,
、
、
、
为快变量,
为分岔参数;系统(8)~(9)构成慢子系统,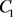 、
为慢变量。本文通过调节内源参数
、
的取值,依据Hopf点在分岔曲线上的不同位置,得到了两种不同类型的簇放电模式 [6] 及其转迁机制。
、
为慢变量。本文通过调节内源参数
、
的取值,依据Hopf点在分岔曲线上的不同位置,得到了两种不同类型的簇放电模式 [6] 及其转迁机制。
3.2.1. 经由“fold/homoclinic”滞后环的“fold/homoclinic”型簇放电
当 时,系统(4)~(9)中房室1的放电模式如图3(左)膜电位的时间历程图,快子系统(4)~(7)的平衡点分岔曲线以慢变量
作为分岔参数,并将两房室系统(4)~(9)的相平面图
附加其上,得到图3(右)快慢动力学分岔图。
时,系统(4)~(9)中房室1的放电模式如图3(左)膜电位的时间历程图,快子系统(4)~(7)的平衡点分岔曲线以慢变量
作为分岔参数,并将两房室系统(4)~(9)的相平面图
附加其上,得到图3(右)快慢动力学分岔图。
图3(右)包含一条“Z”型分岔曲线,分岔曲线上支存在一个Hopf分岔点,使得稳定焦点转变为不稳定平衡点,然后通过LP分岔点转至分岔曲线的中支出现鞍点,最后,通过第二个LP分岔点进入分岔曲线的下支,出现稳定结点。其中,分岔曲线中支的H点为中性鞍点,不是分岔点。由此可知,簇放电的静息状态通过第二个LP分岔点转变为放电状态,同时,放电状态通过分岔曲线中支的鞍点同宿分岔转变为静息状态,因此,此簇放电为“fold/homoclinic”型簇放电。而且,分岔曲线下支跃迁到分岔曲线上支也是通过第二个LP分岔点,而分岔曲线上支跃迁到分岔曲线下支则是通过分岔曲线中支的鞍点同宿分岔,因此,此簇放电为经由“fold/homoclinic”滞后环的“fold/homoclinic”型簇放电。
3.2.2. 经由“fold/homoclinic”滞后环的“Hopf/homoclinic”型簇放电
当
时,系统(4)~(9)中房室1的放电模式如图4(左)膜电位的时间历程图所示,快子系统(4)~(7)的平衡点分岔图以慢变量
为分岔参数,同时将系统的相平面图
附加其上,得到图4(右)快慢动力学分岔图。
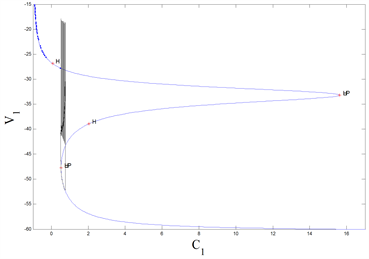
Figure 3. The “fold/homoclinic” bursting via the “fold/homoclinic” hysteresis loop in the system (4)~(9) when
. (Left): Time series of the membrane potential; (Right): Fast-slow dynamics bifurcation diagram
图3. 当
时,系统(4)~(9)中经由“fold/homoclinic”滞后环的“fold/homoclinic”型簇放电。(左):膜电位的时间历程图;(右):快慢动力学分岔图

Figure 4. The “Hopf/homoclinic” bursting via the “fold/homoclinic” hysteresis loop in the system (4)~(9) when
. (Left): Time series of the membrane potential; (Right): Fast-slow dynamics bifurcation diagram
图4. 当
时,系统(4)~(9)中经由“fold/homoclinic”滞后环的“Hopf/homoclinic”型簇放电。(左):膜电位的时间历程图;(右):快慢动力学分岔图
图4(右)展示了两条分岔曲线:L形分岔曲线构成了分岔曲线的上支,存在一个Hopf分岔点,随着分岔参数
的增加,由稳定焦点转变为不稳定平衡点;抛物线形分岔曲线构成了分岔曲线的中支和下支,并且该抛物线形平衡点分岔曲线包含一个LP分岔点,由构成分岔曲线中支的鞍点经过LP分岔点转变为构成分岔曲线下支的稳定结点。由此可见,上静息态经由分岔曲线上支的Hopf分岔点消失同时出现反复放电状态;放电状态碰到分岔曲线中支的鞍点同宿分岔跃迁到下静息态,因此,此簇放电为“Hopf/homoclinic”型簇放电。又知,分岔曲线下支通过LP分岔点处的鞍结分岔跃迁到分岔曲线上支,并且分岔曲线上支通过鞍点同宿分岔跃迁到分岔曲线下支,因此,此簇放电为经由“fold/homoclinic”滞后环的“Hopf/homoclinic”型簇放电。
4. 多房室神经元Chay模型
神经元的形态结构丰富多样,包含髓鞘等多种生理特征存在,因此,运用房室模型刻画这些不同的形态和特性,能够更精准地模拟大量的非线性特征和节律编码。基于螺旋神经节神经元的空间几何形态和组成结构,构建两种多房室神经元Chay模型,进行信息传递、退化机制等方面的数值模拟,并且探究中枢突结构对生物信息编码的影响。不仅对多房室神经元Chay模型进行了包括最大电位、频率编码等多方面的理论神经计算,同时,刻画了神经元模型在不同刺激、脱髓、中枢突结构缺失等多种情况下的放电模式,对退化机制、刺激位点的搭配等特性进行了解释和验证。
4.1. 15房室神经元Chay模型
I型螺旋神经节神经元占总数的90%以上,有髓鞘,而II型螺旋神经节神经元的占比不到10%,无髓鞘。因此,运用理论模型进行数值模拟,可以研究不同神经元模型信息传递的特点以及节律编码的丰富模式。如第2节所言,未包裹髓鞘的房室用Chay模型描述,包裹髓鞘的房室则为双电缆结构,据此,基于I型螺旋神经节神经元 [19] [22] 的形态结构,构建15房室神经元Chay模型,研究理论模型的信息传递特点、刺激位点搭配以及退化机制等规律。
4.1.1. 两类神经元模型放电模式的比较
神经冲动的时间编码和频率编码都是发放过程的重要载体,对于信息的识别和传递至关重要。为此,本文将信息的传递过程用第一动作电位潜伏期(first spike latency, FSL)、发放率(firing rate, FR)以及最大电位(
)来描述。FSL表示信息传递起始部分的特征,刻画了生成第一动作电位的持续时间,与神经元模型的信息表达密切相关,有助于各种异常发放的判断。FR和
体现了信息传递的整体情况,FR作为一种频率编码方式,反映了放电活动的强度,被普遍应用于脑科学研究中,
作为发放过程中膜电位的相关指标,是判断各种神经元模型发放状态的基本参考依据。
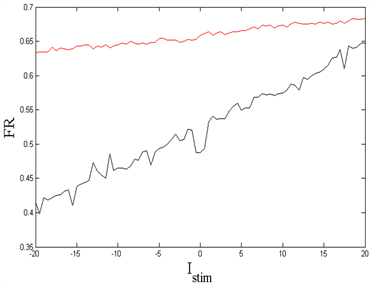
Figure 5. (Left): First spike latency (FSL) of two kinds of neuron models when
; (Right): Firing rate (FR) of two kinds of neuron models when
. Red: Model with myelin. Black: Model without myelin
图5. (左):当
时,两种神经元模型的第一动作电位潜伏期(FSL);(右):当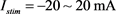 时,两种神经元模型的发放率(FR)。红色:髓鞘模型,黑色:非髓鞘模型
时,两种神经元模型的发放率(FR)。红色:髓鞘模型,黑色:非髓鞘模型
如图5(左),随着外界刺激
的增加,两类神经元理论模型的FSL均稳步下降,即外界刺激越大,第一动作电位生成越快。并且髓鞘模型比非髓鞘模型反应更加灵敏,尤其是当刺激增加时,髓鞘模型能够更快地辨别。如图5(右),整体上两类神经元理论模型的FR都随着刺激的增加而增大,并且髓鞘模型比非髓鞘模型的发放率大。
4.1.2. 外界刺激对不同房室的影响
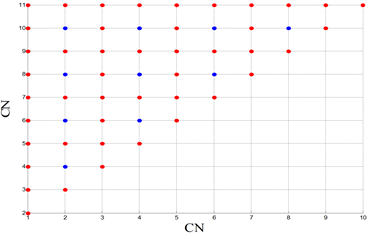
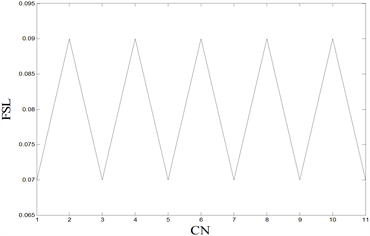
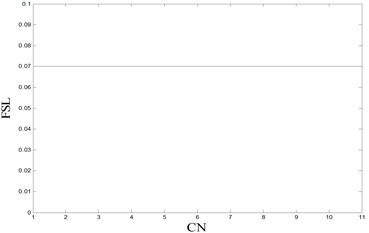
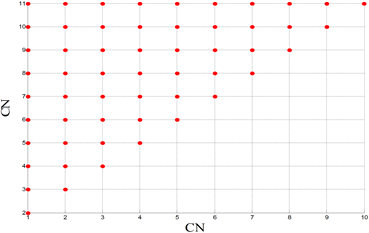
Figure 6. Comparisons of FSL under different stimulations. (Top left): Only one compartment is stimulated, and the abscissa is the compartment number (CN) for current stimulation. (Top right): Two compartments are stimulated at the same time. The abscissa and ordinate are the compartment number (CN) stimulated by the current. The FSL of the red dot is 0.07 s, and the FSL of the blue dot is 0.09 s. (Bottom left): Nine compartments are stimulated at the same time. The abscissa and ordinate are the compartment number (CN) without current stimulation, and the FSL of the red dot is 0.07 s. (Bottom right): Ten compartments are stimulated at the same time, and the abscissa is the compartment number (CN) without current stimulation
图6. 不同刺激情况下的FSL对比。(左上):只对一个房室进行刺激,横坐标为进行电流刺激的房室编号(CN)。(右上):同时对两个房间进行刺激,横、纵坐标均为受到电流刺激的房室编号(CN),红色点的FSL为0.07 s,蓝色点的FSL为0.09 s。(左下):同时对九个房间进行刺激,横、纵坐标均为没有受到电流刺激的房室编号(CN),红色点的FSL为0.07 s。(右下):同时对十个房室进行刺激,横坐标均为没有受到电流刺激的房室编号(CN)
为了探究不同房室对于外界刺激的敏感性,因此本文对周围突的不同房室进行直流正电刺激,得到各种情况下的第一动作电位潜伏期FSL的取值,如图6所示。从图6(上)可知,当进行单房室刺激时,如果对髓鞘房室进行外界直流电刺激,FSL会增加;当进行两房室刺激时,如果两房室均为髓鞘房室,FSL也会增加。因此,本文猜想:只要对非髓鞘房室进行刺激,FSL就会减小。为了证明这一猜想,本文分别进行了五房室刺激,以及六房室刺激,数值模拟发现:当进行五房室刺激时,只存在一种情况对五个髓鞘房室全刺激,FSL呈现较大值,在其他情况下,FSL均呈现较小值;当进行六房室刺激时,一定会刺激到非髓鞘房室,所以FSL都呈现较小值,猜想成立。同时,图6(左下)的九房室刺激以及图6(右下)的十房室刺激都验证了这一猜想,由于任何情况下,均存在刺激位点处于非髓鞘房室,因此,FSL都呈现较小值。
因此,本文能够确定,第一动作电位潜伏期FSL的大小与刺激郎飞结(非髓鞘房室)的有无相关,而与神经元房室的搭配无关,并且只要对郎飞结进行刺激,FSL就会呈现较小值,神经元模型生成第一动作电位的持续时间更短。
4.1.3. 神经元模型的退化模拟
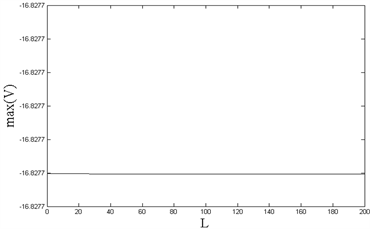
Figure 7. (Left): Changes of FSL with L (length of demyelination); (Right): Changes of the maximum potential of the soma with L (length of demyelination)
图7. (左):FSL随L(髓鞘脱落长度)的变化;(右):胞体的最大电位随L(髓鞘脱落长度)的变化
环境刺激或者自然衰老所带来的退化,表现形式有:髓鞘的逐步脱落以及周围突不同程度的消失 [19] [23] [24]。为了研究退化程度的影响机制,本文用髓鞘脱落长度来数值模拟退化程度,探究了脱髓鞘对神经元模型的FSL、最大电位等信息编码的影响。
由于周围突最短的一段髓鞘长度为210 μm,因此本文将髓鞘脱落的长度限制在0~200 μm的范围内。图7(左)中,FSL不随髓鞘的脱落而改变,始终保持一个定值;由图7(右)可知,胞体的最大电位随着髓鞘脱落程度的加剧,在小范围内呈现基本不变的趋势。因此可以推测得到,髓鞘脱落并非一定造成神经元模型内部信息编码能力的减弱。通过对脱髓鞘的研究,探讨了其对于信息传递编码的影响。
4.2. 131房室神经元Chay模型
螺旋神经节神经元具有复杂的空间形态结构以及大量中枢突分叉,不同中枢突组成部分传递的信息被耳蜗核的不同结构接收,并且表现出不同的反应。根据重构的小鼠Ⅰ型螺旋神经节神经元的几何形态将其划分成了131个房室,构建131房室模型结构,同时,以Chay模型模拟每个神经元房室的发放活动,研究内、外源参数和中枢突结构的改变对于模型节律编码的影响。
4.2.1. 不同参数的敏感性
为了研究不同电生理参数和外界刺激对于131房室神经元Chay模型放电节律的影响,选取FSL、FR、
作为信息编码的指标,进行如下数值计算。
如图8所示,神经元模型的FSL不随最大电导
而变化,始终保持定值0.09 s;但是FSL随着外界刺激
的增大出现阶段性的改变,当
时,FSL仍然保持0.09 s,直至
时,FSL减小至0.08 s,随后保持不变。因此,神经元模型的FSL不会受到内源参数
的影响,但是当外界刺激
超过某个正阈值时,神经元模型生成第一动作电位的速度更迅敏。
由图9可知,当外界刺激
变化时,胞体的发放率并不呈现较明显的变化规律,在小范围内无序地上下波动,而当外界刺激
接近0值时,中枢突末梢的发放率迅速降至最低值0.5667,当外界刺激
远离0值时,中枢突末梢的发放率在区间
内小范围波动。当最大电导
增加时,胞体和中枢突末梢的发放率整体上均呈现减小的趋势。因此可知,外界刺激
和内源参数
对神经元模型各房室会造成不同的影响:内源参数
对神经元模型各房室FR的影响具有相同倾向;而外界刺激
对于中枢突末梢的发放率影响更明显,并且在
时出现骤变。
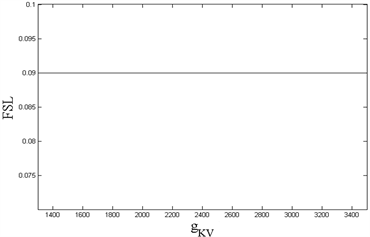
Figure 8. (Left): Changes of FSL with
. (Right): Changes of FSLwith
图8. (左):FSL随 的改变。(右):FSL随
的改变
的改变。(右):FSL随
的改变

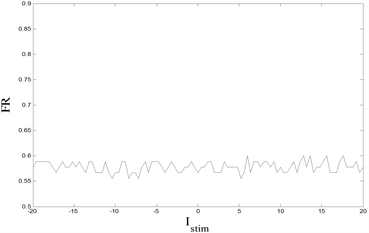
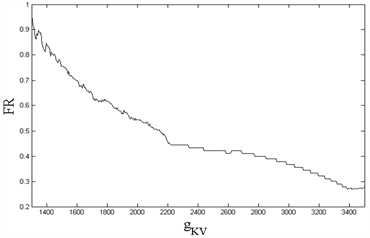
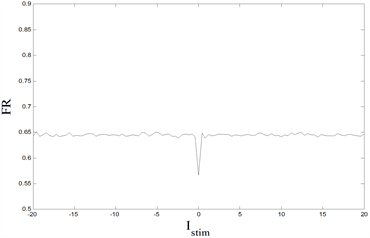
Figure 9. Changes of FR in various parts of neuron model with parameters. (Top left):
diagram of the soma; (Top right):
diagram of the soma; (Bottom left):
diagram of the terminal button of the central axon; (Bottom right):
diagram of the terminal button of the central axon
图9. 神经元模型各部位的FR随参数的改变。(左上):胞体的
图像;(右上):胞体的
图像;(左下):中枢突末梢的
图像;(右下):中枢突末梢的
图像
如图10所示,当外界刺激
增加时,房室1(首房室)的最大电位呈现局部抛物线、整体上升的趋势,房室2(胞体)的最大电位在小范围内呈抛物线型下降,房室6(中枢突主要分叉点)的最大电位对于
不敏感,始终保持不变。当内源参数
增加时,房室1、2、6的最大电位均呈现抛物线下降趋势,并且房室2、6的最大电位曲线几乎完全重合,房室1的最大电位始终高于另外两个房室。由此可知,外界刺激
对神经元模型各房室的最大电位造成不同影响,并且较前端房室的最大电位变化更明显,而各房室的最大电位受到内源参数
的影响具有相同倾向性,均抛物下降。
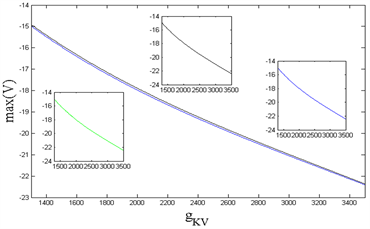
Figure 10. (Left): The variation of maximum potential of compartment 1, 2, and 6 with Istim; (Right): The variation of maximum potential of compartment 1, 2, and 6 with gKV. Among them, black: compartment 1, green: compartment 2, blue: compartment 6, and in the two figures, the blue and green curves partially overlap due to similar values
图10. (左):房室1、2、6的最大电位随着Istim的变化;(右):房室1、2、6的最大电位随着gKV的变化。其中,黑色:房室1,绿色:房室2,蓝色:房室6,且在两图中,由于取值相近,蓝、绿曲线部分重合
在神经冲动传递的过程中,内、外源参数的改变均会给生物信息编码带来丰富的变化,展现多种放电模式之间的转化:外界刺激
的改变给神经元模型带来的影响较大,但是不具有相同规律性,并且
的有无会给信息传递状态带来骤变;而内源参数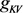 虽然对于神经元模型的FSL影响不大,但是对于各房室的发放率以及最大电位的影响较大并且各房室的变化具有相同倾向性。
虽然对于神经元模型的FSL影响不大,但是对于各房室的发放率以及最大电位的影响较大并且各房室的变化具有相同倾向性。
4.2.2. 同步差
为了定量地探讨生物信息传递过程中神经元模型的全局发放模式以及两参数的协同影响,本文引入了同步差 [25],定义如下:
其中,N为房室数。
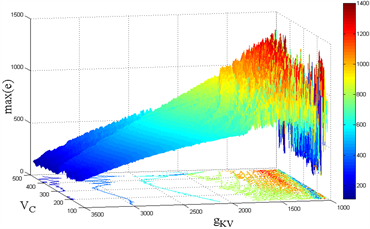
Figure 11. Changes of maximum synchronization error caused by different parameters. (Left):
diagram; (Right):
diagram
图11. 不同参数引起最大同步差的改变。(左):
图像;(右):
图像
如图11(左),当外界刺激接近
时,最大同步差(
)发生骤变,迅速降至最低点,当外界刺激
远离0值时,最大同步差均在小范围内波动;而可逆电位
对于最大同步差的影响亦在小范围内波动。如图11(右),相比较
的改变,
的变化会给最大同步差带来更规律的影响,随着
的减小,最大同步差先增大后减小。并且,
比
对于最大同步差的影响更大。
综合上述各种信息编码方式的研究,本文发现对于外界刺激
的有无,信息传递的起始部分以及整体过程都有强烈的变化;内源参数
的改变则对信息传递的整体过程产生影响,且由于是每个神经元房室都包含的生理因素,因此给各房室带来的变化具有相同的倾向性。
4.2.3. 中枢突结构对放电模式的影响
左右耳螺旋神经节神经元传递的神经冲动被两侧的耳蜗核接收,继而将接收的生物信息传递到中枢神经系统。耳蜗核这一神经核团由耳蜗前腹侧核(AVCN)、耳蜗后腹侧核(PVCN)和耳蜗背侧核(DCN)三部分共同组成,研究发现,耳蜗核不同区域对外界刺激的信息传递具有不同的反应。为了探究信息传递的影响,本小节对分别去掉不同中枢突结构的131房室神经元Chay模型进行信息编码的神经计算,考察这三部分结构对信息传递的重要性。
将分别去掉AVCN、PVCN、DCN对应的部分中枢突之后的神经元模型和正常神经元模型进行不同编码方式的比较,数值模拟发现,改变神经元模型的拓扑结构对于中枢突末梢FR的影响较为明显,得到图12。当最大电导
变化时,只有在区间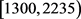 和
内,部分中枢突的去除才会对中枢突末梢的FR产生不同影响,在正常情况的取值周围上下波动。当调节外界刺激
时,去掉AVCN对应的部分中枢突之后,FR在正常情况的取值周围上下波动,而去掉DCN和PVCN对应的部分中枢突之后,中枢突末梢的FR普遍高于正常情况的取值。由模拟结果可知,当外界刺激
变化时,中枢突的结构变化会对中枢突末梢的FR产生显著影响,发放强度会改变;当内源参数
在特定区间
和
内变化时,中枢突结构的变化才会影响模型的发放强度。
和
内,部分中枢突的去除才会对中枢突末梢的FR产生不同影响,在正常情况的取值周围上下波动。当调节外界刺激
时,去掉AVCN对应的部分中枢突之后,FR在正常情况的取值周围上下波动,而去掉DCN和PVCN对应的部分中枢突之后,中枢突末梢的FR普遍高于正常情况的取值。由模拟结果可知,当外界刺激
变化时,中枢突的结构变化会对中枢突末梢的FR产生显著影响,发放强度会改变;当内源参数
在特定区间
和
内变化时,中枢突结构的变化才会影响模型的发放强度。
因此,当中枢突结构发生改变时,神经元模型结构的改变对于信息传递的过程产生了影响,同时,当外界刺激
变化时,PVCN和DCN对应的部分中枢突的去除,对于神经元模型的影响具有相同的倾向性。

Figure 12. (Left):
diagram of the terminal button of the central axon in four cases; (Right):
diagram of the terminal button of the central axon in four cases. Among them, black: normal case, green: remove parts of central axon corresponding to AVCN, blue: remove part of central axon corresponding to DCN, red: remove part of central axon corresponding to PVCN
图12. (左):四种情况下中枢突末梢的
图像;(右):四种情况下中枢突末梢的
图像。其中,黑色:正常状况,绿色:去掉AVCN对应的部分中枢突,蓝色:去掉DCN对应的部分中枢突,红色:去掉PVCN对应的部分中枢突
5. 讨论
为了研究房室化神经元Chay模型的非线性分岔现象和放电节律模式,本文基于螺旋神经节神经元的空间结构,构建了具有形态的两房室神经元Chay模型和多房室神经元Chay模型,进行动力学分析、神经计算。
在第3节中,构建两房室神经元Chay模型,进行非线性动力学分岔分析。首先,运用峰峰间距和簇簇间距得到了加周期分岔等分岔序列结构,判定:除了在
等分岔点处,以及
所产生的混沌状态下,两房室均是峰发放或周期性簇发放的。最后,将慢变量
作为分岔参数,通过快慢动力学分岔分析,得到了经由“fold/homoclinic”滞后环的“fold/homoclinic”型簇放电、经由“fold/homoclinic”滞后环的“Hopf/homoclinic”型簇放电这两种簇放电模式及其转迁机制。
在第4节中,构建了两种多房室神经元Chay模型:1) 对15房室神经元Chay模型进行数值分析。首先通过FSL、FR等编码节律证明了髓鞘对于产生和传递神经冲动的优越性。然后,证实了刺激非髓鞘房室有助于提高神经元模型的第一动作电位生成速度。最后,解释了脱髓鞘对神经元模型放电特性的影响。2) 探究131房室神经元Chay模型的放电节律模式。首先,对于FSL,胞体和中枢突末梢的FR,房室1、2、6的最大电位这三类编码方式,研究发现,内源参数
对各房室对应指标的影响具有相同倾向性,而外界刺激
的有无使得神经冲动的传递发生骤变。接着,考察了外源参数
和内源参数
对最大同步差的影响:随着内源参数
的减小,最大同步差先增大后减小;外界刺激
越接近0,最大同步差越小。最后,中枢突结构改变对于信息传递过程中中枢突末梢的FR造成更大影响,并且当外源参数
变化时,PVCN和DCN对应的部分中枢突缺失,具有相同倾向性的影响。
本文探讨了房室化神经元Chay模型的非线性动力学分析和神经计算,得到了两房室神经元Chay模型和多房室神经元Chay模型丰富的放电节律模式及其转迁机制。同时,用理论模型数值模拟发放模式和节律编码,验证并解释了神经元模型的信息传递特点和退化机制等。除此之外,还可以进一步考虑房室化神经元Chay模型的余维2分岔分析、分岔曲线和分岔点的动力学分析等。也可以向模型中添加噪声、时滞等因素,模拟更复杂环境下的神经元模型,对不同环境状态下的神经元模型进行动力学行为研究。
参考文献
附录