1. 引言
临界现象在各领域中广泛存在,它描述了复杂系统在演化过程中的突变行为。对于复杂系统,往往难以建立解析模型或进行重复实验;而系统的静态状态参量在突变前也难以观察到显著改变。所以前人建立起了一套基于系统的动态状态参量来预测系统突变的理论,即临界点理论 [1]。临界点理论背后的数学机理是微分方程的分叉,临界点理论给出的典型临界信号包括系统扰动的方差增大,自相关时间增长等等。
为了适应生物信息领域中的高通量表达技术的发展,由临界点理论演变而产生了动态网络生物标志物(DNB)理论 [2] [3] [4]。经典的临界点理论要求基于长时间序列来进行分析;相反地,在高通量表达数据集合中,每次测量取得大量变量值,而测量次数相对较少。一个典型的高通量表达数据集合,在几个时间点上各自进行数次重复,总共包含几十到几百次测量,而每次测量同时取得上万个变量值。
在DNB理论中,所有基因被视作节点来构成一个网络,基因表达水平之间的相关程度结合外部给出的先验信息确定网络的边。DNB理论认为如此大的一个网络不可能同步越过临界点,即总会有一个子网络率先越过临界点,而后带动整个网络翻转,这个子网络就称为DNB。可以通过识别DNB来探测网络的临界状态。DNB子网络在临界时刻表现出三项普遍特征:1) DNB中基因表达水平的波动普遍增大,理想情形中将会增大到无穷;2) DNB中基因表达水平的波动相关性普遍增强,理想情形中皮尔逊相关系数(PCC)的绝对值将趋近1;3) DNB中的节点与DNB之外节点间的波动相关性普遍减弱,理想情形中PCC将会减小为0。DNB在其它时刻不表现出显著特征。在DNB子网络的临界特征中,我们关注后两项描述相关性的特征。
PageRank是一个受到广泛研究的算法,在不同应用情景下有着多样的具体形式 [5]。基本地,PageRank算法就是求取如下迭代的平衡点:
(1)
其中
是向量,作为迭代变量,它的平衡点
就是PageRank算法的输出,称为PageRank向量;
是标准化之后的邻接矩阵,记标准化之前的邻接矩阵为
,它包含了网络信息,它的
元
表示了节点i到节点j之间的连接强度;
是悬挂向量,它是标准化邻接矩阵时的副产品,用于对全零行进行异常处理;
是个性化向量,没有约束,
除以它的各分量之和得到
,使
满足各分量之和为1;
是阻尼系数,传统上取0.85,本文也遵从该传统。
我们期望通过较高的PageRank值来识别DNB子网络。DNB中的节点两两紧密相关,这一特征有利于获得较高的PageRank值。另一方面,DNB子网络与网络剩余部分相关减弱,这一点不利于我们确定DNB,因为理论上我们不能从网络上定位一个脱离网络的小集团。综合这两点,我们的方法对DNB理论模型提出了一个额外要求:DNB节点的度大于全网络平均值。考虑理想的DNB,即DNB中节点两两连接,与DNB之外的节点没有连接;此时DNB中节点的度就是DNB的大小。这一要求等价于DNB在全网络的占比不能小于邻接矩阵密度。这意味着我们的算法受制于DNB的大小,无法定位过小的DNB。但在实际应用中,这一要求通常是得以满足的。
2. 方法
2.1. 从PCC矩阵提取邻接矩阵
在每一测量时间点,由此刻的数次重复测量,可以直接计算基因表达水平之间的PCC矩阵
。考虑两个正态分布的无关随机变量,它们之间的皮尔逊相关系数r具有如下分布:
(2)
这里n是重复数目,
是
维的T分布;我们取r的单边概率0.050分位点为
。
映射为邻接矩阵的过程中,
中绝对值小于
的元素归0,绝对值大于
的元素映射到[0,1]区间:
(3)
对于实验数据,我们引入STRING网络 [6] 为外部参考,只采用STRING网络中存在的边;即
中元素若在STRING网络中没有对应边,则令为0。
2.2. 抑制网络中的背景结构
由于DNB的特征仅在临界时刻表现出来,我们需要尝试排除网络中所有时间点均存在的背景结构的影响:
(4)
这里
是
在所有参考时间点上的平均值;如果数据包含对照组,参考时间点就是对照组中的所有时间点,如果数据没有给出对照组,参考时间点就是全体时间点;
以及
分别代替
以及
参与PageRank运算以及作为PageRank输出。取
为中间变量,这一调节可以分为两部分来看待;
用于抑制背景边:如果某一条边总是存在,那么对应的
比较大,此时我们降低它的强度;
以及
一起抑制背景中的中心节点:如果一个节点的度始终比较大,那么对应的
较大,此时我们降低它的PageRank值输出。
2.3. 弥合悬挂节点的不连续性
邻接矩阵
是按行归一化的。普遍的方法是,用每一行的元素之和去除该行所有元素,这样归一化之后矩阵的行和为1。作为异常处理,全0行保持不变,对应节点标记为悬挂节点。悬挂向量
中,对应悬挂节点的分量取1,其余取0。这样,当节点在是否悬挂的状态之间切换时,会导致PageRank向量出现不连续变动。针对这个问题,文献中提出了邻接矩阵的另一种归一化方法 [7] :取
为一个小的常数,用
去除
的第i行,对应的悬挂向量分量取为
。我们将采用后者,因为我们在连续变化的PCC上划定了一个阈值来提取邻接矩阵,故而希望弥合这一阈值带来的不连续性。我们取
为式(2)中分布的单边0.049分位点,再经式(3)映射得到的值。
2.4. DNB子网络中的PageRank值
根据DNB理论,非临界时刻,模型网络是一个大而稀疏的整体,而临界时刻的模型网络可以分为两部分:一部分是小而紧密相关的DNB网络,另一部分是稀疏的非DNB网络,两者间相对独立。所以我们所要做的就是把一个小而紧密相关的子网络从大而稀疏的背景网络之中识别出来。
考察一个子网络中各节点的PageRank值之和E,有如下关系 [8] :
(5)
是由个性化向量产生的PageRank值,
和
分别是通过边输入和输出的PageRank值,
和
分别是子网络中经由悬挂节点向全网逸散的PageRank值以及由全体悬挂节点逸散而来的PageRank值。对DNB子网络:由于内部紧密相关,所以
是0;又由于DNB相对独立,
和
都小,理想情况下是0。
实践中发现也不大,虽然
使得E增大,对我们的算法有利。这样
, 取遍DNB中所有节点。
我们希望DNB网络中的节点具有较高的PageRank值,从而可以将其挑选出来。因此,我们将个性化向量
取为
。一方面我们要求DNB中节点的度大于全网络平均值,另一方面DNB节点中相关性也较大。这样
中对应DNB的分量较大,从而使得DNB子网络中PageRank值的均值较全网络高。
2.5. 渐进PageRank方法
我们仍然不能简单地通过选取PageRank值最高的节点来确定DNB。对于较大的稀疏网络,一个普遍成立的经验规律是,PageRank值分布在高端有幂次衰减的长尾 [9]。这意味着尽管DNB节点具有高于平均的PageRank值,但是仍会被非DNB网络的PageRank值分布的长尾所淹没,因为DNB只占全网络的一小部分。因此,我们采取了另一种思路:循环地运行PageRank算法,不断舍去PageRank值低的节点来最终确定DNB。DNB节点的PageRank值总体偏大,虽然不足以直接选出,但是可以保证在筛选中幸存。DNB中的节点,
中对应分量较大,相邻节点的PageRank值也较大,所以具有较高PageRank值。非DNB网络中PageRank值较高的节点,来源于同时与大量低PageRank值节点的偶然连接。所以,当低PageRank值节点不断被舍去时,前者PageRank值依然较高,而后者不再具有较高的PageRank值。这样最终剩下来的节点就是DNB。
最为稳妥的方式是,每次丢掉PageRank值最低的一个节点。但是出于计算上的实践,我们选取了一个阈值
。每次运行PageRank算法后舍去PageRank值低于
的节点;这里n是当前剩余节点数目,
是为了确保循环过程能够停下来而设定的停止阈值,取为最初节点数目的0.05。
的作用是:当n小于
后逐渐放松筛选条件,直到没有节点被舍去时终止运算。
2.6. DNB评价指标
通过上面的渐进PageRank算法,我们在每个时刻挑选出了一个DNB。而后,我们需要建立一个DNB评价指标来选出最显著的DNB作为有效DNB。我们选择DNB子网络中边的平均强度作为DNB评价指标:
(6)
这里n是DNB的节点数目。有效DNB所对应的时刻就是我们所探测到的临界时刻。
3. 结果
3.1. 数值模拟
我们首先用数值模拟来检验我们的方法。一般的动力学系统可以表述为
;假设它初始收敛于0,而后在参数
逐渐改变时失稳。考虑它在奇点0附近的稳定性,我们只需要讨论它在奇点0处的线性化系统
:当
负定时系统稳定;当最大特征值接近0时,系统逐渐失稳。考虑一个有限的时间间隔,令为1,有
;差分方程的形式便于生成模拟数据。再假设
可以对角化为
。其中
是随机生成的稀疏矩阵,与
无关。而对角矩阵
中也仅有第一个元素
依赖于
;其余元素取随机生成的不太接近0的负值。在数值模拟的一系列时间点中,
逐渐趋近于0。这样,在临界点时,
是主特征值,它无限趋近于0;
的第一列是主特征向量,它的非零元对应DNB。我们通过如下迭代来生成模拟数据集合:
(7)
是迭代变量,初值为全0;
是随机向量,各分量独立服从高斯分布,用于在迭代过程中引入随机性。在模拟数据集合中,我们的渐进PageRank算法成功定位了DNB并给出了临界预警信号。在图1中我们展示了DNB评价指标随主特征值 的变化;在绝大多数模拟数据中,DNB评价指标在
趋于0时趋近于1,成功地指示了临界点。
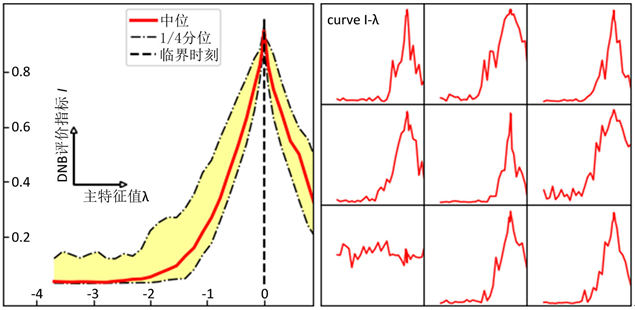
Figure 1. DNB indication for simulations (left: a synthesis result, right: specific curves)
图1. 数值模拟的DNB评价指标曲线(左:综合展示,右:部分具体曲线)
3.2. 实验数据
接下来,我们将算法应用于两组实验数据中,复现了文献中报道的方法给出的结果 [2] [3] [4]。第一个数据集合来源于光气引起小鼠肺部损伤的实验(GEO accession number: gse2565) [10]。在实验中,小鼠首先在光气中暴露20分钟,然后每间隔一段时间进行高通量表达测量。12 h时刻观察到小鼠的死亡率在50%~60%之间,24 h时刻观察到小鼠的死亡率在60%~70%之间,这意味着绝大多数死亡事件发生在前12 h。我们的渐进PageRank算法确定的临界时刻是8 h,见图2。我们的结果与实验现象相符。
第二组数据源于HRG诱导MCF-7人体乳腺癌细胞分化的实验(GEO accession number: gse13009) [11] [12]。HRG诱导的分化过程,与EGF诱导的增殖过程,在前90 m很相似,在90 m之后表现出显著不同。我们确定的临界时刻是90 m,与实验现象相符,见图3。
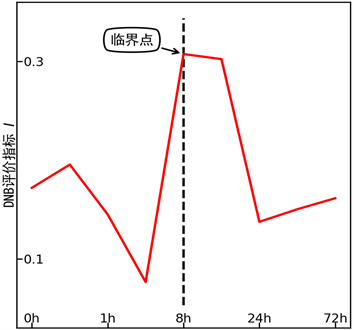
Figure 2. DNB indication for the experiment of mouse lung injury
图2. 小鼠肺部损伤实验的DNB评价指标曲线
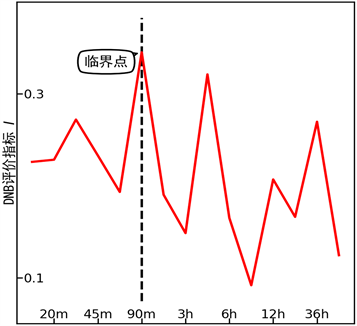
Figure 3. DNB indication for the experiment of HRG induced differentiation on MCF-7 human breast cancer cells
图3. HRG诱导MCF-7人体乳腺癌细胞分化实验的DNB评价指标曲线
4. 讨论
相比于文献中报道的基于DNB理论的临界点探测方法:在提取DNB的步骤中,我们用渐进PageRank算法替代了聚类算法;在评价DNB有效性的步骤中,我们用单纯基于波动相关性的指标,替代了同时基于波动相关性以及波动幅度的指标。因而在算法性能上,我们取得了三点显著改进。
首先是在DNB识别能力上的改进。DNB理论中并没有对DNB的大小做具体规定,但是DNB占整个网络比值太小以至于不能识别,是实践中不得不面对的问题。文献中的解决方案是,在应用DNB模型之前,先依据差异表达以及波动幅度增大倍数等非网络方法来对高通量表达数据中的基因表达水平进行预筛选,以使得DNB模型涵盖的节点数目适合。文献中的预筛选非常激进,基因芯片给出的数目超过一万的基因表达水平,经过预筛选后剩余不足一千,这意味着信息的大量流失。文献中DNB占模型网络比值普遍超过百分之二十,这意味着聚类方法的识别能力很弱。在我们的渐进PageRank方法中,DNB占模型网络比值小于百分之十,这意味着我们在预筛选步骤中保留了更多的节点。这是相当大的进步,虽然距离我们舍去预筛选步骤,直接应用网络算法的目标还有相当大的距离。
第二方面的改进在于DNB评价指标中排除了对波动幅度的依赖。文献中的DNB评价指标是:
。其中,SD是DNB中所节点波动标准差的均值,
是DNB中节点两两PCC的均值,
是DNB中的节点与DNB之外节点PCC的平均,
是一个防止分母为0的小量。由于每个基因本身的背景波动幅度不同;一个高通量表达数据中的基因表达水平x,在参与运算之前,往往要经过一个
形式的标准化,然后用
代替x参与后续运算,a和b是随基因而异的。显然这样的标准化会直接影响SD的取值,但是不会影响PCC的取值,所以我们认为在DNB评价指标中排除了对波动幅度的依赖是一项改进。
第三,DNB的特征只会在临界时刻表现出来;该文的方法对DNB网络中各个时间点都存在的固有结构进行了抑制;而在文献中基于聚类的方法中,每个时刻的数据是独立参与运算的。
基金项目
本文受广东省基础与应用基础研究基金资助(No. 2019B151502062)。