1. 引言及主要结果
假设读者熟悉亚纯函数Nevanlinna值分布理论的基本内容及相关标准符号(见参考文献 [1] [2] [3])。特别的,
表示整函数f的级,当
时,称f为有穷级整函数。
设 是复平面上的整函数,定义其差分算子为
是复平面上的整函数,定义其差分算子为
,
.
2018年,王琼、扈培础 [4] 研究了杨重俊提出的如下猜想:
猜想1:如果
是超越整函数,对某个正整数k,如果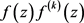 是周期函数,则
也是周期函数。
是周期函数,则
也是周期函数。
王琼、扈培础 [4] 证明了以下特殊情形,猜想1是正确的,他们证明了:
定理1:如果 是超越整函数,对某个正整数k,如果
是周期函数,则
是超越整函数,对某个正整数k,如果
是周期函数,则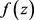 也是周期
也是周期
函数。
注1:显然
,即定理1说明猜想1当
时是正确的。
2019年,刘凯等人 [5] 研究了在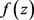 有非零Picard例外值的情形,猜想1是正确的。
有非零Picard例外值的情形,猜想1是正确的。
定理2:如果
是超越整函数,
是
的一个Picard例外值,对某个正整数k,如果
是周期函数,则
也是周期函数。
对于定理2,要求
,自然会问,当
时,定理2结论是否成立?本文研究了该问题,证明了以下结论。
定理3:如果
是有穷级超越整函数,0是
的一个Picard例外值,对某个正整数k,如果 是以c为周期的函数,则
是以c为周期的函数,则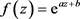 ,其中
是两个常数,并且
,即
是以
,其中
是两个常数,并且
,即
是以
2c周期的周期函数。
另外,我们将定理2中的导数替换成差分,证明了如下结论。
定理4:如果 是有穷级超越整函数,d是
是有穷级超越整函数,d是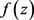 的一个Picard例外值,如果
是周期函数,则
也是周期函数。
的一个Picard例外值,如果
是周期函数,则
也是周期函数。
2. 一些引理
引理2.1 ( [6])设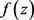 是一个有穷级亚纯函数,c是非零常数,则有
是一个有穷级亚纯函数,c是非零常数,则有
 .
.
引理2.2 ( [2])设
除
之外是非常值亚纯函数,并且满足 ,和存在一个常数
,对任意的,
时,均有
,和存在一个常数
,对任意的,
时,均有
,  ,
,
,
,
其中
是测度有穷的集合。
则
。
3. 定理3的证明
由0是
的Picard例外值,且
是有穷级超越整函数,因此存在非常数多项式
,使得
,显然
。经简单计算,可得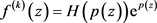 ,其中
,其中 是关于
是关于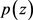 的微分多项式。显然
,否则
,得
是一个次数不超过
的多项式,这与
是超越整函数矛盾。引理2.1可得
,
的微分多项式。显然
,否则
,得
是一个次数不超过
的多项式,这与
是超越整函数矛盾。引理2.1可得
, 。
。
另外,因为
是周期函数,不妨设其周期为c,则有
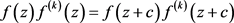 .(1)
.(1)
将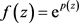 ,
,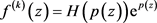 代入(1)式,可得
代入(1)式,可得
.
从而有
.
当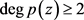 时,
.
时,
.
,
矛盾。
所以
,令
,其中
. 则
,
,代入(1)式,可得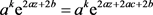 ,所以
,即得
,所以
,即得 。
。
定理3证明完毕。
4. 定理4的证明
由d是  的Picard例外值,且
的Picard例外值,且 是有穷级超越整函数,因此存在非常数多项式
,使得
,显然
。经简单计算,可得
,若
,则显然
是以c为周期的周期函数,以下考虑
的情形。
是有穷级超越整函数,因此存在非常数多项式
,使得
,显然
。经简单计算,可得
,若
,则显然
是以c为周期的周期函数,以下考虑
的情形。
另一方面,因为
是周期函数,不访设其周期为
,则有
.(2)
将
,
代入(2)式,
当
时,有
. (3)
可断言:
, (4)
 . (5)
. (5)
若不然,由(3)式及引理2.1,引理2.2,可得
.
矛盾。
令
,
,
。
情形1。
。则
,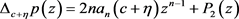 。其中
。其中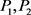 是次数不超过
是次数不超过 的多项式。可知
均是次数为
的多项式。由(5)式及引理2.2,可得
,或者
,或者
,矛盾。
的多项式。可知
均是次数为
的多项式。由(5)式及引理2.2,可得
,或者
,或者
,矛盾。
情形2。
。则
, ,
,代入(5)式,可得
,
,代入(5)式,可得
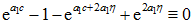 ,即
解方程,有
,或
。即
是以c或
为周期的周期函数。进一步的,若
,结合(4)式,可得
,即
解方程,有
,或
。即
是以c或
为周期的周期函数。进一步的,若
,结合(4)式,可得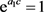 ,或
,即
是以c或
为周期的周期函数。
,或
,即
是以c或
为周期的周期函数。
当
时,有
. (6)
与上述讨论类似,可得
是以c或
为周期的周期函数。
定理4证明完毕。
基金项目
国家自然科学基金青年资助项目(11901119, 11701188);广东教育厅科研项目(2017KTECX130)。