1. 引言
国家电网省级通信管理系统(Transportation Management System, TMS)在资源管理、实时监控、运行管理方面发挥了巨大作用,同时也积累了大量数据,其中蕴藏价值亟待挖掘。由于数据规模的膨胀,TMS系统中的数据具有分散存储、多个字段缺乏相应解释、数据噪声较多、空值较多等特点,使得数据分析变得异常困难。因此需要在原数据集的基础上进行数据整理与特征选择,为后续深度处理做好准备。决策树(decision tree)模型 [1] 是机器学习中一种较为常见的分类模型,不仅适用于分类问题,同时也适用于回归问题,其基本实现方法包括CART [2] 、ID3 [3] 、C4.5 [4] 等。特征选择是一个对所有数据中包含的属性进行择优的一个过程,最终获取到所有特征的相对重要排名并进行选择。决策树模型具有很多优点,包括模型学习代价低、时间效率高、实现方式多样且易于改进、能对离散数据或连续数据都有特定的处理能力等。然而,决策树模型也包含了决策效果单一、对数据样本的依赖程度很高、无法避免陷入局部最优效果中等等。Adaboost算法 [5] 和Bagging算法 [6] 都是决策树模型的改进算法。为完善Bagging算法,LEO Breiman提出了随机森林(Random Forest) [7];在采样过程中,使用有放回的boostrapping技术 [8],同时改进了决策节点特征选择的集合。与Bagging中将所有数据的属性作为可选特征集合不同,随机森林则随机选取所有数据属性的一个非空子集作为候选特征集合。因此,随机森林可以巧妙地避免过拟合的问题。
针对TMS系统数据进行特征选择目前没有通用方法,本文尝试在TMS系统条件下,使用多棵决策树集成的随机森林来对数据进行特征选择,以不同的度量标准与结果评判进行比对,从而择优选出适合 TMS系统大数据的特征选择方法,并通过实验进行分析验证。
2. 随机森林模型
2.1. 特征划分选择
在进行特征划分时,需要考虑每一个特征的重要程度,因此往往需要对每一个特征进行重要性度量。一般使用信息增益 [9] 和基尼指数 [10] 两种方法对特征进行重要性度量。
给定样本集
,属性集
。假设当前样本集合D中第k类样本所占的比例为
,其中|𝑌|为当前样本集合的分类标签数目。同时,假定离散属性a有V个可能的取值
,若使用a来对样本集D进行划分,则会产生V个分支节点,其中第v个分支节点包含了D中所有在属性a上取值为
的样本,记为
。用
表示样本集中样本数目,
表示D中所有在属性a上取值为
的样本数目 [11]。
1) 基于信息增益度量的特征划分选择 信息增益的计算过程:
信息增益的计算过程:
计算当前样本集D的信息熵。
(1)
计算属性a对样本集D进行划分所获得的信息增益。
(2)
这里,
越小,表示样本集D的纯度越高;
越大,表示用属性a来划分样本集D所获得的纯度提升越大,属性a的重要性越高。
2) 基于基尼指数度量的特征划分选择
基尼指数的计算过程:
计算当前样本集D的基尼值。
(3)
计算属性a对样本集D进行划分后的基尼指数。
(4)
其中,
越小,表示数据集的纯度越高,选择使得划分后基尼指数最小的属性作为最优划分属性,即
(5)
2.2. Bagging算法
Bagging算法是基于自助采样法(boostrap sampling)的一种集成学习方法。给定一个包含n个样本数据的样本集,从中随机取出一个样本放入采样集,之后再把该样本放入原样本集,这样便使得该样本在下一次采样过程中仍有被选中的可能性。重复n次上述采样过程,便获得一个包含n个样本的采样集,且原数据集中的部分样本可能多次出现在采样集中,部分样本可能从未出现。样本在n次采样过程中始终不被采到的概率为
,取极限可以得到:
(6)
通过自助采样,原样本集中约有36.8%的样本从未出现在采样集中,可以将这部分样本用作测试集。
2.3. 随机森林
随机森林(Random Forest)是由多棵决策树集成的组合分类器,本质上是Bagging的一个扩展。随机森林模型采用了双重随机法,一是使用Bagging方法随机获取每棵决策树的训练子集,二是随机选择一定数量的划分属性进行特征分裂,使得最终集成的学习器泛化性能大大提升。
给定由k棵决策树
构成的随机森林以及两个随机向量X,Y,则有:
带外(Out Of Band, OOB)数据,原样本集中约有36.8%的样本从未出现在自助采样集中出现,可以将这部分样本用作测试集,即用作验证集来对泛化性能进行“带外估计”。用
来表示决策模型
中实际用到的训练样本集,用
来表示对样本X的“带外预测”分类标签,有
(7)
随机森林泛化误差的带外估计为
(8)
随机森林模型的建立过程:
① 确定原数据样本集中的样本个数N。
② 确定原数据样本集中的样本特征数目M。
③ 从原数据样本集中随机采样得到T个训练样本子集。
④ 确定决策树的节点属性划分时需要使用的特征个数m,且
。
⑤ 使用T个训练样本子集,根据确定的划分使用特征个数m,用信息增益、基尼指数等特征重要性度量方法,生成T棵决策树。
⑥ 将T棵决策树进行集成,对预测结果采用简单投票法来得出最终分类结果。
3. 随机森林模型在TMS特征选择中的应用
TMS系统数据具有较高维度,且存在噪声,在进行分类任务之前,必须进行特征选择,否则分类器的精度以及学习效率会异常低下。目前针对TMS系统数据尚需通过人工对照标记来选择学习任务的特征,具有强烈的主观性,缺乏科学的理解与支撑。在此背景下,针对TMS系统数据的特点,用随机森林模型进行特征选择,并分析基于决策树数目、基于特征划分标准、基于特征划分候选子集中的最大特征数等多个参数对模型结果的影响,提出优化的TMS系统数据的随机森林特征选择方法。
经过对TMS系统数据的提取与存取发现,其累积了大量半结构化数据和非结构化数据,例如值班记录、方式信息、方式单附件、故障报告、“三措一案”等,但是缺少非结构化数据处理与分析能力,其中蕴含价值无法挖掘。同时,TMS系统基于传统数据库构建,主要用于实时事务处理,强调及时、安全地将用户操作记录保存下来(处理事务次数多,但每次涉及数据量都比较大),明显存在不足。
TMS系统数据可大致分为实时告警类、维护管理类、资源管理类、设备画像类及外部数据源五类 [12]。由于数据规模的膨胀,TMS系统中的数据具有不同省份分散存储、多个字段缺乏相应解释、数据噪声较多、空值较多等特点。基于上述数据特点,需要对TMS系统的数据进行收集与预处理,并选择适合的模型与方法进行训练,最后进行可视化展现。对于大数据的数据分析关键技术,需要基于其数据类型、数据规模的特点,可以从三个方面着手:
① 从大数据的清洗、整理、抽样以及特征选择的角度入手,将大数据小数据化。
② 开展大数据下各种分类聚类算法的研究,根据具体问题选取特定的机器学习算法。
③ 开展大数据的并行算法,将传统的数据挖掘、数据分析算法用分布式并行实现,提高效率。
3.1. 基于决策树数目
随机森林的模型越好,其特征重要性排名越为准确,但是时间代价和空间代价也会变大。为了在满足一定性能的前提下选取最为合适的决策树数目,可遵照如下原则执行:
① 在决策树数目较少的范畴,进行迭代测试,观察决策树数目与随机森林模型准确率的关系。
② 在决策树数目达到一定高度后,进行以一定步长的迭代测试,观察决策树数目与随机森林模型准确率的关系。
③ 衡量决策树数目与随机森林模型准确率的关系,择优选择在满足一定准确率的条件下,决策树数目最为合适的大小。
3.2. 基于特征划分标准
决策树模型内部节点进行特征划分时,需要考虑每一个特征的重要程度,因此往往需要对每一个特征进行重要性度量。决策树模型常常使用信息增益和基尼指数来对特征进行重要性度量 [13]。为了选取最适合于TMS系统的特征划分标准,可遵照如下原则执行:
① 使用信息增益的特征划分准则,进行随机森林的建模,得到特征重要性程度的排名,以及该模型的准确率。
② 使用基尼指数的特征划分准则,进行随机森林的建模,得到特征重要性程度的排名,以及该模型的准确率 [14]。
③ 对比信息增益与基尼指数所进行特征划分对TMS系统随机森林模型的准确率影响,选取较之更适合于TMS系统的特征划分方法。
3.3. 基于特征划分候选子集中的最大特征数
随机森林较于Bagging的最大优点,就是在进行节点划分时随机选取特征划分候选子集,在大数理论的支持下,很大程度上非常巧妙地避开了“过拟合”的问题。因此需要确定节点划分候选子集中的最大特征数。当划分候选子集中的最大特征数为1时,无法进行特征重要性度量;当划分候选子集中的最大特征数等于所有特征数目时,随机森林模型的基决策树的构建过程与传统决策树的构建过程无异 [15]。
为了选取最适合于TMS系统的特征划分候选子集中的最大特征数,可遵照如下原则执行:
① 在随机森林模型构建时,选取的特征划分候选子集中的最大特征数,从1到n进行迭代测试,其中n为数据样本集的所有特征数目。
② 对比在特征划分候选子集中的最大特征数不同的情况下,随机森林模型的准确率以及该模型下的特征重要性排名,从而选取最适合于TMS系统的特征划分候选子集中最大特征数。
3.4. 基于特征重排后模型的准确率变化
OOB样本对评估模型准确率有着重要的作用,因此可以通过将OOB样本中的每一个特征的所有特征值进行重排,来影响重排后的随机森林模型准确率。通过衡量重排前后模型准确率的变化幅度,就可以获得该特征对于随机森林模型的重要程度。如果是相对重要的特征,则该特征的特征值顺序变动后,会大幅度降低原模型的准确率;如果是相对不重要的特征,则该特征的特征值顺序变动后,对原模型的准确率不会产生较大的影响。
为了衡量特征重排后对模型的准确率变化指标所产生的特征重要性排名,本文遵照如下原则执行:
① 使用原始数据样本集训练得到随机森林模型,记录其模型准确率。
② 使用OOB样本对每一个特征进行所有特征值重排,通过对比重排前后随机森林模型准确率的变化大小,得到新的特征重要性排名。
进行特征选择后,TMS系统需要进行的后续学习任务多为分类问题,于是大部分情况下可以直接使用训练出来的随机森林模型作为分类模型。通过分析基于决策树数目、基于特征划分标准、基于特征划分候选子集中的最大特征数、基于特征重排后模型的准确率变化等多个参数对随机森林模型应用于TMS特征选择模型结果的影响,可以训练得到一组最适合于TMS系统的特征重要性排名。为了对该排名进一步完善,并得到一个准确率更高的随机森林模型,将选取特征重要性排名中靠前的特征,重新训练得到一个新的随机森林模型以及新的一组特征重要性排名。具体流程为:
① 使用基于决策树数目、基于特征划分标准、基于特征划分候选子集中的最大特征数、基于特征重排后模型的准确率变化的参数,得到一个随机森林模型和一组特征重要性排名。
② 对得到的特征重要性排名进行截枝,得到最为重要的前几个特征。
③ 使用新的特征重新训练随机森林模型,并得到一个新的随机森林模型和一组新的特征重要性排名。
④ 可以使用新的随机森林模型对后续的分类任务进行分类。
4. 实验与分析
4.1. 实验数据
本文实验数据来自于依托某项目获得的某省电网TMS系统数据,为了实验方便,抽取了其中的业务类型汇总表进行实验分析,其表结构如表1所示。


Table 1. Summary of business types
表1. TMS业务类型汇总表
4.2. TMS系统数据预处理
通过业务类型汇总表的225,506条数据,对EquipmentType字段进行分类预测。为了实现分类任务,首先通过对表字段以及表数据分析,人工去除了一些无用字段,如ObjectID、ObjectDispidx、WholeName、Name等;考察到有一些大量为空的字段,如END_DATE、BuyDate、DispObj、END_DATE等,将之去除;最后去除隐藏字段,包括TEST1、TEST2、TEST3、TEST4。最终,剩下用于模型训练属性集为{A_SITE_ID,Z_SITE_ID,PAR_SYS,DISP_ORGA,PAR_ZONE,IS_FIBER_BUZ,BUZ_TYPE, DISPATCH_ LEVEL,SERVICE_STATE,CHANNEL_CAPACITY,BUZ_RATE},由27个字段压缩为11个字段,标签集为{EquipmentType}。
4.3. 实验分析
实验包括决策树数目对比、特征划分标准对比、特征划分候选子集中的最大特征数对比、特征重排的留出法验证以及特征截枝前后对比,并由此得到了每种参数指标中最适合于TMS系统数据进行特征选择的值;最后形成了最适合于TMS系统特征选择的随机森林模型,并通过实验得到了最终的特征选择结果。所有出现的参数score代表随机森林模型的全样本集标签分类预测准确率,参数oob_score_代表随机森林模型的OOB样本标签分类预测准确率。
4.3.1. 决策树数目对比
小数目集使用了1~10棵决策树进行迭代测试,大数目集使用了10~200以步长为10棵决策树进行了迭代测试。当考虑随机森林模型的OOB样本标签分类预测准确率oob_score_时,发现其随着决策树的增大,变化明显程度大大高于score,进一步说明oob_score_对随机森林准确率的分析具有重要的作用,见图1。

Figure 1. The influence of decision tree number on score and oob_score_
图1. 决策树数目对score和oob_score_的影响
当决策树数目以步长为10棵在10~200之间变化时,随机森林模型准确率有一定的上升趋势,当决策树数目大于70棵时,模型准确率的上升已趋近于0,如图2所示。
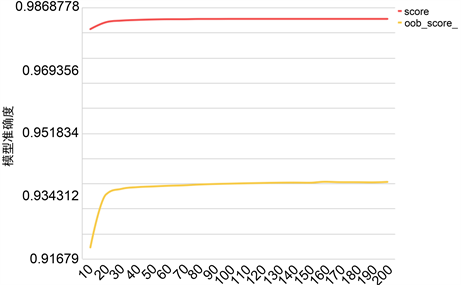
Figure 2. Effect of decision tree number on accuracy of random forest model in large data sets
图2. 决策树数目在大数据集时对随机森林模型准确率的影响
因此,决定使用决策树数目为70棵的随机森林作为最终模型。当决策树数目为70棵时,得到的特征重要性程度如图3所示,其中BUZ_TYPE最为重要,而BUZ_RATE重要程度为0。

Figure 3. The importance degree of features when the number of decision trees is 70
图3. 决策树数目为70棵时的特征重要性程度
4.3.2. 特征划分标准对比
在决策树数目以步长为10棵在10~200之间变化时,分别使用基于信息增益和基于基尼指数对节点进行特征划分完成随机森林的建模。
如图4所示,当选取决策树数目为70棵时,基于信息增益与基于基尼指数的特征划分标准所产生的最终特征重要性程度,在分布上基本一致,在数值上略有差别,如关于特征BUZ_TYPE的重要程度,基于信息增益所得到的值为0.26,而基于基尼指数所得到的值为0.24。这也说明,无论采用哪种特征划分标准,对最终分类模型的构建具有重要性的特征占比始终较大;反之,一些不重要的特征占比始终较小,如BUZ_RATE,对模型的重要程度始终为0。

Figure 4. The importance of characteristics of different criteria
图4. 不同划分标准的特征重要性程度
4.3.3. 特征划分候选子集中的最大特征数对比
在TMS系统数据的业务类型汇总表中,去除一些冗余或无用的字段后,剩余11个字段。因此,在随机森林的基决策树进行节点划分时,可以考虑使用1~11个特征作为特征划分候选子集。
如图5所示,当最大特征数从1到11变化时,随机森林模型的准确率先上升后下降,这是由于当特征数较少时,基决策树无法选择最为合适的特征来进行划分;但当特征数过多时,随机森林模型的基决策树与传统决策树越来越相近,当最大特征数等于所有特征数时,随机森林模型的基决策树与传统决策树无异,因此,其模型准确率会有所下降。
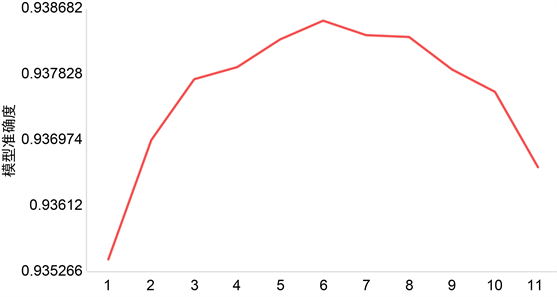
Figure 5. Effect of maximum characteristic number on model accuracy
图5. 最大特征数对模型准确率的影响
对于TMS系统数据,当特征划分子集中的最大特征数为6时,所得到的随机森林模型准确率最高。因此,针对TMS系统的数据,我们选取6为特征划分候选子集中的最大特征数。
当特征划分候选子集中的最大特征数为6棵时,得到的特征重要性程度如图6所示,其中特征重要性排在前三的分别是BUZ_TYPE、DISP_ORGA和PAR_SYS。

Figure 6. The degree of feature importance when the maximum feature number is 6
图6. 最大特征数为6时的特征重要性程度
4.3.4. 特征重排的留出法验证
通过衡量特征重排前后模型准确率的变化幅度,可以获得该特征对于模型的重要程度。模型准确率的变化幅度越大,则特征越重要,反之若模型准确率变化幅度越小,则特征越不重要。
采用留出法进行实验,即每次留出30%的数据作为测试样本。当进行了100次留出法验证后,得到的特征重要性程度如图7所示。本次排名中,特征BUZ_RATE和特征SERVICE_STATE的重要性程度都为0,而基于前三个参数所得到的特征重要性排名中只有特征BUZ_RATE为0;同时,最重要的特征BUZ_TYPE的重要程度已经超过了0.3,而基于前三个参数所得到的特征重要性排名中特征BUZ_TYPE的重要程度均在0.25左右。由此可以得到,使用特征重排前后模型准确率的变化幅度来衡量特征重要性程度,能够让重要的特征变得更为重要,让不重要的特征变得更为不重要,因此该方法略优于其他特征衡量方法。
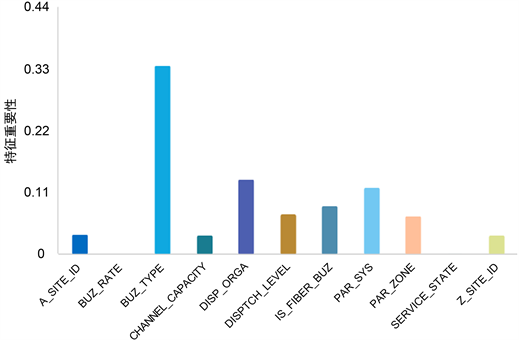
Figure 7. Importance degree of feature based on feature rearrangement
图7. 基于特征重排的特征重要性程度
4.3.5. 特征截枝前后对比
对随机森林模型训练后得到的特征重要性排名进行截枝,取得最为重要的几个特征,再次进行随机森林模型的训练,最终得到一组更为优化的特征重要性排名和一个可直接用于分类任务的随机森林模型。用基于信息增益、基于基尼指数、基于特征重排后模型准确率变化三个维度来对特征截枝,得到截枝前后随机森林模型的准确率变化。采用的截枝策略为:当特征的重要性程度小于0.1时,将其截取去除。基于信息增益、基于基尼指数、基于特征重排后模型准确率变化来对特征进行截枝,所截取的特征不一样,参见表2。

Table 2. Three-dimensional characteristic truncation results
表2. 三个维度的特征截枝结果
如果使用随机森林模型的oob_score_来衡量其准确率,可以看出无论是基于信息增益、基于基尼指数还是基于特征重排后模型准确率变化进行特征截枝,随机森林模型的oob_score_均变大,但基于特征重排后模型准确率变化进行特征截枝后,其模型准确率提升更为明显,参见图8。
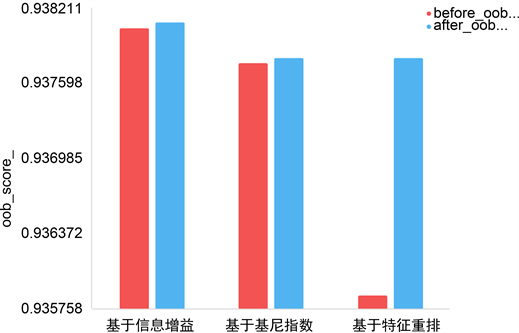
Figure 8. Comparison of oob models before and after feature truncation in three dimensions
图8. 三个维度的特征截枝前后模型oob_score_对比
通过对TMS系统数据预处理后,针对随机森林应用于TMS特征选择的不同方法进行了实验对比与分析,最终选择出来的最适合TMS系统数据的随机森林特征选择模型如下:
① 随机森林模型的决策树数目取值为70。
② 对于随机森林模型中的每一棵基决策树,使用信息增益的方法来对节点进行特征划分。
③ 在基决策树的每一个节点进行特征划分时,随机选取的特征划分子集中的最大特征数为6。
④ 在对特征的重要性程度进行排名时,采用特征重排后随机森林模型准确率变化程度作为衡量标准。
⑤ 对得到的特征重要性排名进行截枝,去除特征重要性程度小于0.1的特征,并用剩余的特征重新进行①至④的过程,最终得到优化过的特征重要性排名和一个可以直接用于分类任务的随机森林模型。
对该模型进行实验后,得到特征重要性排名,参见表3。因此,在使用随机森林模型对TMS系统进行特征选择后,得到的三个重要特征为:BUZ_TYPE、DISP_ORGA和PAR_SYS。

Table 3. Importance ranking of features
表3. 特征重要性排名
同时,我们进行实验后得到新的随机森林模型的score为0.983598327673,oob_score_为0.937970145976,可以直接用于后续的分类任务。
5. 结语
本文在对TMS系统的数据特点进行分析后,对其进行数据预处理操作,并将随机森林模型应用于特征选择。为了训练得到适合于TMS系统的特征选择模型,本文对决策树数目、特征划分标准、特征划分候选子集中的特征数、特征重排的留出法、特征截枝进行了重点分析,衡量了这些参数对模型结果的影响,从而择优选择出最适合于TMS系统数据的特征选择方法,并对该方法进行了验证。