Steiner对称化下双变量凸体算子stH(·+·)的性质

doi:10.12677/PM.2020.102017

期刊菜单

Steiner对称化下双变量凸体算子st_H(·+·)的性质
The Properties of the Bivariate Convex Body Operator st_H(·+·) under Steiner Symmetrization

DOI: 10.12677/PM.2020.102017, PDF, HTML, XML, 下载: 584 浏览: 3,245
作者: 姜亦芳：陕西师范大学，数学与信息科学学院，陕西西安
关键词: 凸体；Steiner对称；Minkowski加法；Convex Bodies； Steiner Symmetrization； Minkowski Addition

摘要: 本文利用凸体的Steiner对称化的性质，结合Minkowski加法刻画了一个双变量凸体算子，并研究了该算子的相关性质。给凸体关于给定的Rⁿ中的超平面H作Steiner对称可以得到一条很重要的性质，即设C和D是n维欧式空间Rⁿ中的两个凸体，有包含关系：st_H(C+D)⊆st_HC+st_HD。该性质在利用Steiner对称化方法得到经典的Brunn-Minkowski不等式和经典的等周不等式的简洁证明中起到了关键作用。本文就是在该性质的基础之上刻画了双变量凸体算子st_H(·+·)及其性质。

Abstract: In this paper, a bivariate convex body operator and its properties will be characterized by using Steiner symmetrization method and Minkowski addition. Steiner symmetrization of convex bodies with respect to a given hyperplane H in Rⁿ has a very important property that if the sets C and D are two convex bodies of Euclidean n-space Rⁿ, there is a inclusion relation: st_H(C+D)⊆st_HC+st_HD. This property plays a key role in the concise proof of the classical Brunn-Minkowski inequality and the classical isoperimetric inequality by using the Steiner symmetrization method. In this paper, on the basis of this property, we further characterize the bivariate convex body operator st_H(·+·) and its properties.

文章引用：姜亦芳. Steiner对称化下双变量凸体算子st_H(·+·)的性质[J]. 理论数学, 2020, 10(2): 106-110. https://doi.org/10.12677/PM.2020.102017

1. 引言

在凸几何分析中，一个更对称的凸体在许多情况下具有更好的几何或分析性质。因此，研究将凸体转化为更对称的凸体的对称化方法是非常有意义的，比如文献 [1] 中对Steiner，Minkowski，Schwarz和中心对称进行了研究。而在众多凸体的对称化方法中，Steiner对称化可能是解决凸几何领域中的问题最为强大的对称化方法，比如，利用Steiner对称化方法可以得到经典的Brunn-Minkowski不等式和经典的等周不等式的简洁证明 [2]，其他相关的应用可以查阅文献 [1] [3] - [9]。这是因为Steiner对称化方法具有很多优良性质，比如，保凸性、保体积性、表面积不增性、周长不增性等。在Brunn-Minkowski理论中，Minkowski加法是其重要的组成部分，比如经典的Brunn-Minkowski不等式就是建立在Minkowski加法的基础之上。

Steiner对称化关于Minkowski加法有一条非常重要的性质：设凸体 $C, D \in K^{n}$ ，对于给定 $R^{n}$ 中的超平面H，有以下的包含关系(即命题2.1 ii))：

$s t_{H} (C + D) \subseteq s t_{H} C + s t_{H} D,$

这条性质在利用Steiner对称化方法得到的经典的Brunn-Minkowski不等式和经典的等周不等式的简洁证明中都起到了至关重要的作用。本文就是以此为切入点，刻画了由该性质衍生出的双变量凸体算子 $s t_{H} (\cdot + \cdot)$ 及其相关性质，例如连续性、单调性等。

上述出现的概念和符号在下文中有详尽的说明。

2. 预备知识

本文首先回顾Steiner对称和Minkowski加法的定义和相关性质。我们以下的讨论基于n维实欧几里德向量空间 $R^{n}$ ，以o为原点， $〈 \cdot, \cdot 〉$ 为欧几里得空间的标准内积， $| \cdot |$ 为该内积诱导的范数。

设 $K^{n}$ 为 $R^{n}$ 上全体凸体(紧凸集)组成的集合(简称凸体空间)， $C^{n}$ 为 $R^{n}$ 上所有非空紧子集组成的集合(简称真凸体空间)，H为 $R^{n}$ 中的任意超平面。令 $C \in K^{n}$ ，则C关于超平面H的Steiner 对称化为 $s t_{H} C$ 的定义 [1] 为：对于每一条垂直于H的直线L，并且满足 $C \cap L \neq \emptyset$ ，将线段 $C \cap L$ 沿着L移动，直到 $C \cap L$ 的中点落在H上，这样得到的所有线段的并就是 $s t_{H} C$ 。显然， $s t_{H} C$ 关于超平面H(镜面)对称。

给定一个凸体 $C \in K^{n}$ ，我们给出一些刻画凸体的几何量的概念，直径 $d i a m (C) = \sup {| x - y | : x, y \in C}$ ，外接圆半径 $R (C) = \inf {R \in R : x + R B^{n} \supseteq C, x \in C}$ ，内切圆半径 $r (C) = \sup {r \in R : x + r B^{n} \subseteq C, x \in C}$ 。其中 $B^{n} = B (o, 1) = {x \in R : | x | \leq 1}$ 为 $R^{n}$ 中的实心单位球。

下面我们列出有关Steiner对称的性质定理，这些性质会在后文的证明中用到。

命题 2.1 [2] 凸体 $C, D \in K^{n}$ ，关于给定的超平面H的Steiner对称化具有以下的性质：

i) $s t_{H} C \in K^{n}$ ；

ii) $s t_{H} (C + D) \subseteq s t_{H} C + s t_{H} D$ ；

iii) 若 $C \subseteq D$ ，则有 $s t_{H} C \subseteq s t_{H} D$ ；

iv) 映射 $s t_{H} : C^{n} \to C^{n}$ 是连续的；

v) $d i a m (s t_{H} C) \leq d i a m (C)$ ；

vi) $R (s t_{H} C) \leq R (C)$ ；

vii) $r (s t_{H} C) \geq r (C)$ 。

现在叙述Minkowski加法的定义和性质。Minkowski加法和数乘的定义为：

$C + D = {x + y : x \in C, y \in D}$ ,

$λ C = {λ x : x \in C}$ ,

其中 $C, D \in K^{n}$ ， $λ$ 为一个实数。设 $x \in R^{n}$ ，集合 $x + D (= {x + y : y \in D})$ 可以看作D沿向量x的平移，则Minkowski加法的另外一种定义：

$C + D = \underset{x \in C}{\cup} (x + D) = \underset{y \in D}{\cup} (C + y) .$

下面我们列出有关Minkowski加法的性质定理，这些性质将在后文定理的证明中用到。

命题 2.2 [10] 关于集合的Minkowski加法有以下的性质：

i) 若 $C, D \in K^{n}$ ，则 $C + D \in K^{n}$ ；

ii) Minkowski加法作为 $C^{n} \times C^{n}$ 到 $C^{n}$ 的映射是连续的；

iii) 集合 $K^{n}$ 和 $C^{n}$ 关于Minkowski加法构成了交换半群，其单位元为{o}；

iv) 集合 $K^{n}$ 满足消去律，即：若 $C, D, K \in K^{n}$ 并且 $C + K = D + K$ ，则有 $C = D$ ；

v) 集合 $K^{n}$ 满足顺序消去律，即：若 $C, D, K \in K^{n}$ 并且 $C + K \subseteq D + K$ ，则有 $C \subseteq D$ ；

vi) 若 $C \in K^{n}$ ， $\forall λ, μ \in R$ 并且 $λ, μ \geq 0$ ，有 $λ C + μ C = (λ + μ) C$ 。

命题 2.3设 $C_{1}, C_{2}, D_{1}, D_{2} \in C^{n}$ ，并且满足 $C_{1} \subseteq C_{2}, D_{1} \subseteq D_{2}$ ，则有 $C_{1} + D_{1} \subseteq C_{2} + D_{2}$ 。

3. 主要结果

设 $C, D \in C^{n}$ ，H为 $R^{n}$ 中给定的超平面，我们定义如下的算子：

$ϕ (C, D) = s t_{H} (C + D),$

则 $ϕ$ 为 $C^{n} \times C^{n}$ 到 $C^{n}$ 的双变量凸体算子。

定理 3.1在 $ϕ (\cdot, \cdot)$ 在 $C^{n} \times C^{n}$ 上是连续的。

证明考虑 $C^{n}$ 中的收敛序列 ${C_{n}}, {D_{n}}$ 。假设当 $n \to \infty$ 时，两个序列分别收敛于C、D，其中 $C, D \in C^{n}$ 。由Minkowski加法的性质，即命题2.2 i)、ii)，我们可以得到当 $n \to \infty$ 时，有 $C_{n} + D_{n} \to C + D$ 。结合Steiner 对称的连续性，即命题2.1 ii)，可得当 $n \to \infty$ 时，有 $s t_{H} (C_{n} + D_{n}) \to s t_{H} (C + D)$ ，定理得证。

从上面的证明中，我们可以知道该双变量凸体算子 $ϕ (\cdot, \cdot) = s t_{H} (\cdot + \cdot)$ 是具有连续性的，此外，我们也可以证明其同时具有单调性，即在 $C^{n} \times C^{n}$ 上是不减的。

定理 3.2设 $C_{1}, C_{2}, D_{1}, D_{2} \in C^{n}$ ，并且满足 $C_{1} \subseteq C_{2}, D_{1} \subseteq D_{2}$ ，则有 $s t_{H} (C_{1} + D_{1}) \subseteq s t_{H} (C_{2} + D_{2})$ 。

证明由于 $C_{1}, C_{2}, D_{1}, D_{2} \in C^{n}$ ，以及 $C_{1} \subseteq C_{2}, D_{1} \subseteq D_{2}$ ，根据Minkowski加法的性质，即命题2.2 i)和命题2.3，我们可以得到 $C_{1} + D_{1}, C_{2} + D_{2} \in C^{n}$ ，并且 $C_{1} + D_{1} \subseteq C_{2} + D_{2}$ 。结合Steiner对称的性质，即命题2.1 iii)，可得：

$s t_{H} (C_{1} + D_{1}) \subseteq s t_{H} (C_{2} + D_{2}),$

即定理得证。

我们要注意该算子不为线性算子，为此我们举出如下例子：

例3.1设 $R^{2}$ 中的两个凸体 $C = {(x, y) \in R^{2} : 0 \leq x \leq 1, 0 \leq y \leq 1 - x}$ ， $D = {(x, y) \in R^{2} : 0 \leq x, y \leq 1}$ ，令 $H = {(x, 0) \in R^{2} : x \in R}$ ，我们可以证明 $s t_{H} (λ C + D) = λ s t_{H} (C + D)$ ( $λ$ 任意常数)不成立。为此我们可以只需证明当 $λ = 2$ 时，该等式不成立。根据Steiner对称和Minkowski加法的定义，可得： $s t_{H} (2 C + D) = {(x, y) \in R^{2} : y_{2} (x) \leq y \leq y_{1} (x), 0 \leq x \leq 3}$ ，其中

$y_{1} (x) = {\begin{cases} \frac{3}{2}, 0 \leq x \leq 1 \\ - \frac{x}{2} + 2, 1 \leq x \leq 3 \end{cases}$ $y_{2} (x) = {\begin{cases} - \frac{3}{2}, 0 \leq x \leq 1 \\ \frac{x}{2} - 2, 1 \leq x \leq 3 \end{cases}$

同样可得 $2 s t_{H} (C + D) = {(x, y) \in R^{2} : {y^{'}}_{2} (x) \leq y \leq {y^{'}}_{1} (x), 0 \leq x \leq 4}$ ，其中

${y^{'}}_{1} (x) = {\begin{cases} 2, 0 \leq x \leq 2 \\ - \frac{x}{2} + 3, 2 < x \leq 4 \end{cases}$ ${y^{'}}_{2} (x) = {\begin{cases} - 2, 0 \leq x \leq 2 \\ \frac{x}{2} - 3, 2 < x \leq 4 \end{cases}$

显然， $s t_{H} (2 C + D) \neq 2 s t_{H} (C + D)$ ，故而等式 $s t_{H} (λ C + D) = λ s t_{H} (C + D)$ ( $λ$ 任意常数)不成立，即该算子不为线性算子。

下面我们用一些几何量来进一步刻画该双变量凸体算子。

定理 3.3 设 $C, D \in C^{n}$ ，则以下命题是成立的：

i) $d i a m (s t_{H} (C + D)) \leq d i a m (C) + d i a m (D)$ ；

ii) $R (s t_{H} (C + D)) \leq R (C) + R (D)$ ；

iii) $r (s t_{H} (C + D)) \geq r (C) + r (D)$ 。

证明

i) 由直径的定义可得：

$\begin{matrix} d i a m (C + D) = \sup {| x_{1} + y_{1} - (x_{2} + y_{2}) | : x_{1}, x_{2} \in C, y_{1}, y_{2} \in D} \\ \leq \sup {| x_{1} - x_{2} | : x_{1}, x_{2} \in C} + \sup {| y_{1} - y_{2} | : y_{1}, y_{2} \in D} \\ = d i a m (C) + d i a m (D), \end{matrix}$

结合Steiner对称的性质，即命题2.1 v)可得：

$d i a m (s t_{H} (C + D)) \leq d i a m (C + D) \leq d i a m (C) + d i a m (D) .$

ii) 由外接圆的定义，我们可设 $x + R (C) B^{n} \supseteq C, y + R (D) B^{n} \supseteq D$ ，其中 $x \in C, y \in D$ 。根据Minkowski 加法的性质，即命题2.3，可得：

$x + y + (R (C) + R (D)) B^{n} \supseteq C + D .$

进而 $R (C) + R (D) \geq R (C + D)$ 。结合Steiner对称的性质，即命题2.1 vi)可得：

$R (s t_{H} (C + D)) \leq R (C + D) \leq R (C) + R (D) .$

iii) 由内切圆的定义，我们可设 $x + r (C)) B^{n} \subseteq C, y + r (D) B^{n} \subseteq D$ ，其中 $x \in C, y \in D$ 。根据Minkowski 加法的性质，即命题2.3，可得：

$x + y + (r (C) + r (D)) B^{n} \subseteq C + D .$

进而 $r (C) + r (D) \leq r (C + D)$ 。结合Steiner对称的性质，即命题2.1 vii)可得：

$r (s t_{H} (C + D)) \geq r (C + D) \geq r (C) + r (D) .$

证毕。

4. 结语

本文在研究Steiner对称性质的基础之上，结合Minkowski加法，得到了一个双变量凸体算子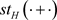，并对其性质展开研究。首先，我们证明了其具有连续性和单调性这样良好的代数性质；其次，我们用直径、内切圆和外接圆这些几何量去刻画该算子，也得到了相应的良好性质。

致谢

本论文是在我导师王拓教授的悉心指导下完成的，从基础知识的学习到论文的选题、参考资料的收集以及论文的修改，每一步都是在王老师的指导下完成的，在此我向我的导师王拓教授表示深切的谢意与祝福。

参考文献

[1]	Bianchi, G., Gardner, R.J. and Gronchi, P. (2017) Symmetrization in Geometry. Advances in Mathematics, 306, 51-88. https://doi.org/10.1016/j.aim.2016.10.003
[2]	Gruber, P.M. (2007) Convex and Discrete Geometry. Springer-Verlag, Berlin Heidelberg, 168-187.
[3]	Klain, D.A. (2011) Steiner Symmetrization Using a Finite Set of Directions. Advances in Applied Mathematics, 48, 340-353. https://doi.org/10.1016/j.aam.2011.09.004
[4]	Leichtweiss, K. (2008) On Steiner’s Symmetrization of Convex Bodies in Non-Euclidean Geometry. Results in Mathematics, 52, 339-346. https://doi.org/10.1007/s00025-008-0315-3
[5]	Mcnabb, A. (1967) Partial Steiner Symmetrization and Some Condition Problems. Journal of Mathematical Analysis and Applications, 17, 221-227. https://doi.org/10.1016/0022-247X(67)90147-3
[6]	Bourgain, J., Lindenstrauss, J. and Milman, V.D. (1989) Estimates Related to Steiner Symmetrizations. Lecture Notes in Mathematics, 1376, 264-273. https://doi.org/10.1007/BFb0090060
[7]	Chlebík, M., Cianchi, A. and Fusco, N. (2005) The Perimeter Inequality under Steiner Symmetrization: Cases of Equality. Annals of Mathematics, 162, 525-555. https://doi.org/10.4007/annals.2005.162.525
[8]	戴进. 凸体的两个几何量在Steiner对称化下的变化及其应用[J]. 数学进展, 2018, 47(5): 767-772.
[9]	孙丽英. 凸体的Steiner对称化的两个定理[J]. 理论数学, 2017, 7(5): 368-372.
[10]	Schneider, R. (2014) Convex Bodies: The Brunn-Minkowski Theory. Cambridge University Press, Cambridge, 139-150.

为你推荐

友情链接