1. 引言
贷款是银行或其他金融机构按一定利率和必须归还等条件出借货币资金的一种信用活动形式,也是金融市场的一种重要活动。对于一份贷款,有很多种还款方式,目前市场上对贷款的主要还款方式有等额本息还款法,等额本金还款法,到期一次还本付息法等。关于借贷以及还款方式的研究有陈悦对贷款的三种主要还款方式进行了简单分析 [1]。王顺等对等额本息和等额本金两种还款方式进行了比较 [2]。吴森等对抵押贷款进行了定价和分析 [3] [4]。Scott与Larry构建了贷款分析系统,对信用风险进行了动态定价 [5]。Christine的文章给出了衡量贷款预期收益的模型,银行之间的竞争迫使银行需要在更大范围内考虑其与客户的整体关系 [6]。Michael与Larry综合考虑了贷款抵押、质押品和期限情况,发展了商业贷款定价模型 [7]。Edward构建的贷款定价模型将贷款价值的评估与借款人信用级别相联系,对贷款现金流进行了估计 [8]。Indra等通过实证观察贷款方法–效率关系,在区域范围内检验了最佳贷款方法 [9]。
但现有的还款方式大都是只依赖于贷款本身,很少考虑还款人自身状态的变化。对于自身资产或者收入波动比较大的借贷者,例如一些收入不确定的中小企业,常规的还款方式往往隐含较大的违约风险。为此我们设计了一种新的灵活的贷款还款方式,其还款强度依赖于借贷人资产,还款额按借贷人还款当时资产的一定比例。即俗称的“有多少还多少”方式。这种还款方式大大减少了借贷人违约的可能性,因此对借方有很强的吸引力,对贷款人来说也有好处,从而具有实际和应用意义。但对于放贷人来说这样的还款方式带来了清款时间的不确定性。至于不确定的借贷人应付部分,贷款人可以通过税收记录等方式进行计算和索还。所以这项设计作为贷款方式的一个补充,具有可行性。而作为会计入账和未来收益的计算,对于贷款的剩余和期望清款时间,我们建立了一个关于剩余贷款的数学模型,在假设借贷方资产满足几何布朗运动的随机过程,运用结构化方法的思想,将贷款的剩余价值看成借款人资产的未定权益,推出公司剩余贷款的期望价值所满足的偏微分方程组,并求解其终值问题得到了解析表达式,然后通过解析表达式分析计算了借贷人期望还清贷款所需时间,并进行数值模拟与分析。
2. 模型的建立
2.1. 模型假设
1) 借贷人连续还付贷款,在t时刻的还款额为 ,
,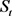 为t时刻借贷人的资产,
为t时刻借贷人的资产,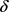 为还款强度,它表示t时刻的还款额占借贷人资产的比例,是一个常数。
为还款强度,它表示t时刻的还款额占借贷人资产的比例,是一个常数。
2) 借贷人资产 的变化满足几何布朗运动:
的变化满足几何布朗运动:
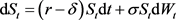 (1)
(1)
其中r为无风险利率, 为公司资产的波动率,
为公司资产的波动率,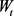 为标准布朗运动。
为标准布朗运动。
3) 借贷人不会违约,在T时刻还清贷款,q为贷款利率,则借贷人的全部负债Q可以表示为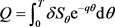 。
。
4) 贷款利率q大于无风险利率r,当贷款利率不为零时,要求借贷人的初始资产大于贷款额度。
5) 用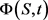 表示t时刻剩余货款的期望价值,满足
表示t时刻剩余货款的期望价值,满足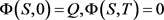 。
。
注:通过数学期望,这里贷款的期望还清时间T是确定的,它是依赖于所求函数,但满足附加条件 ,所以是一个简单的自由边界,可以通过计算求得。
,所以是一个简单的自由边界,可以通过计算求得。
2.2. 贷款的现金流分析
考虑到借贷人自身状态和收入波动的变化,借贷人资产不是一成不变的,具有不可预见性。这里假设借贷人资产的变化满足上述假设2中的随机微分方程 [10]。在还款方式为还款额依赖于借贷人资产的连续还款方式下,t时刻的还款额为 ,与借贷人的资产
,与借贷人的资产 及时间t有关,是不确定的。因此借贷人剩余贷款的价值也与借贷人资产及时间有关,这就带来了还清贷款所需时间的不确定性。根据上述分析,在时间段
及时间t有关,是不确定的。因此借贷人剩余贷款的价值也与借贷人资产及时间有关,这就带来了还清贷款所需时间的不确定性。根据上述分析,在时间段 内,借贷人偿还了部分贷款,即
内,借贷人偿还了部分贷款,即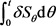 ,考虑到贷款利息,则在t时刻,借贷人剩余贷款本金的期望价值可以用条件期望表示为:
,考虑到贷款利息,则在t时刻,借贷人剩余贷款本金的期望价值可以用条件期望表示为:
 (2)
(2)
2.3. 模型满足的偏微分方程
根据得到的借贷人剩余贷款期望价值的数学表达式(2),利用Feynman-Kac定理 [11],可以得到t时刻借贷人剩余货款的期望价值 满足的偏微分方程:
满足的偏微分方程:
 (3)
(3)
根据偏微分方程理论,问题(3)的解由终值条件即可确定,这是的初值条件是为了求解自由边界T。
3. 模型的求解
3.1. 剩余贷款期望价值的方程解
上述定解问题(3)是一个变系数倒向抛物型偏微分方程的终值问题,仿照Black-Scholes方程的求解方法 [12],先作自变数代换:

转化为常系数抛物型方程的初值问题:
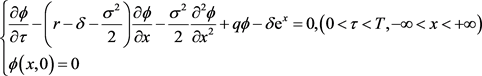 (4)
(4)
根据偏微分方程理论 [13],可求得(4)的解为:
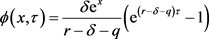 (5)
(5)
代回原来的自变量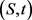 有
有
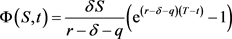 (6)
(6)
这样我们就得到了借贷人剩余贷款期望价值的方程解,其中T为参数。
3.2. 期望还清贷款时间的表达式
根据已知,借贷人全部贷款额为Q,满足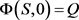 ,代入上述求得的方程解(6)式,可解得期望还清贷款所需时间T的表达式:
,代入上述求得的方程解(6)式,可解得期望还清贷款所需时间T的表达式:
 (7)
(7)
由(7)式,当贷款额度大于初始资产时,期望还清贷款的时间将趋于正无穷,由模型假设借贷人不违
约,因此有 。
。
虽然本文设计的还款方式带来了还清贷款所需时间的不确定性,但是在模型假设及期望意义下,仍然可以通过计算求得期望还清贷款的时间满足的显式表达式。
4. 参数分析
期望还清贷款时间T的表达式(7)中包含S,Q,q,r, 五个参数,其中T与S和Q的关系比较明显:T关与S单调递减,关与Q单调递增。但是T与q,r和
五个参数,其中T与S和Q的关系比较明显:T关与S单调递减,关与Q单调递增。但是T与q,r和 之间的关系则不明显,在下面几小节里我们分别讨论。
之间的关系则不明显,在下面几小节里我们分别讨论。
4.1. T关于q与r的性质分析
命题4.1:当固定参数S,Q,r,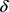 时,T关于q单调递增,即贷款利率越高,期望还清贷款所需的时间越长。
时,T关于q单调递增,即贷款利率越高,期望还清贷款所需的时间越长。
证明:要证明T关于q单调递增,即证明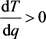 。由(7)式,
。由(7)式,
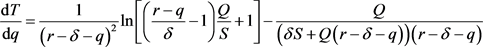 (8)
(8)
不妨令 ,
, ,则有
,则有
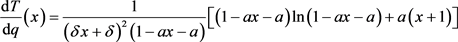 (9)
(9)
因为 ,所以
,所以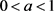 ,
,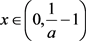 ,此时有
,此时有 ,令
,令
 (10)
(10)
故只需要证明 在定义域内的值恒大于零。计算可得
在定义域内的值恒大于零。计算可得
 (11)
(11)
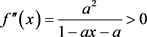 (12)
(12)
且 所以
所以 ,
,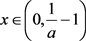 。又因为
。又因为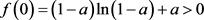 ,
,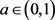 ,所以
,所以 ,
,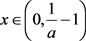 。因此
。因此 ,即T关于q单调递增。
,即T关于q单调递增。
推论4.1:当固定参数S,Q,q,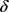 时,T关于r单调递减,即无风险利率越高,期望还清贷款所需的时间越短。
时,T关于r单调递减,即无风险利率越高,期望还清贷款所需的时间越短。
现在我们已经证明了T关于q单调递增,关于r单调递减。但是T与还款强度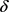 的关系比较复杂,
的关系比较复杂,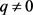 时与
时与 时情况不同,所以下面我们先分析
时情况不同,所以下面我们先分析 时T与
时T与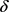 的关系,再讨论
的关系,再讨论 时的情况。
时的情况。
4.2. 时T关于
时T关于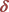 的性质分析
的性质分析
当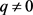 时,模型是一个有息贷款模型。由模型假设,此时借贷人初始资产大于贷款额度,并且还款强度越大,期望还清贷款所需要的时间越短。
时,模型是一个有息贷款模型。由模型假设,此时借贷人初始资产大于贷款额度,并且还款强度越大,期望还清贷款所需要的时间越短。
命题4.2:当固定参数S, Q, r, q时,T关于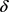 单调递减,即还款强度越大,期望还清贷款所需要的时间越短。
单调递减,即还款强度越大,期望还清贷款所需要的时间越短。
证明:要证明T关于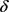 单调递减,即证明
单调递减,即证明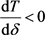 。由(7)式,
。由(7)式,
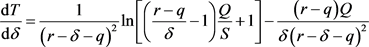 (13)
(13)
不妨令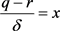 ,
,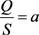 ,则有
,则有
 (14)
(14)
因为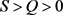 ,所以
,所以 ,
,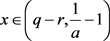 ,此时有
,此时有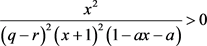 ,令
,令
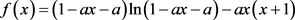 (15)
(15)
故只需要证明 在定义域内的最大值小于零。计算可得
在定义域内的最大值小于零。计算可得
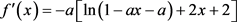 (16)
(16)
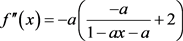 (17)
(17)
令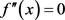 ,可得
,可得 。
。
当 时,对
时,对 的符号进行分析,可得表1。
的符号进行分析,可得表1。
此时, 的符号可统计与表2。
的符号可统计与表2。
因此,当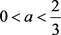 时,
时,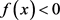 ,即
,即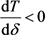 ,即T关于
,即T关于 单调递减。
单调递减。
当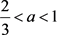 时,同理可证明当
时,同理可证明当 时,
时,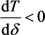 ,即T关于
,即T关于 单调递减。
单调递减。
综上即证明了当固定参数S,Q,r,q (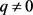 )时,T关于
)时,T关于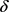 单调递减。
单调递减。
4.3. 时T关于
时T关于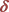 的性质分析
的性质分析
当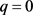 时,模型简化为一个无息贷款模型。由于还款额依赖于还款强度,此时T与
时,模型简化为一个无息贷款模型。由于还款额依赖于还款强度,此时T与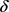 的关系需要分两种情况讨论:当
的关系需要分两种情况讨论:当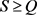 时,T关于
时,T关于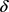 单调递减(见命题4.3);当
单调递减(见命题4.3);当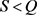 时,T关于
时,T关于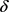 先减后增,T存在最小值(见命题4.4)。
先减后增,T存在最小值(见命题4.4)。
由(7)式,当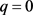 ,借贷人期望还清贷款所需时间可化为:
,借贷人期望还清贷款所需时间可化为:
 (18)
(18)
S为借贷人初始时刻的资产,由模型假设,借贷人不违约,因此,根据(18)式有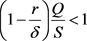 ,且T
,且T
在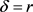 处是连续可导。
处是连续可导。
命题4.3:当固定参数S,Q,r,且 时,T关于
时,T关于 单调递减,即当借贷人初始资产大于贷款额度时,还款强度越大,期望还清贷款所需要的时间越短。
单调递减,即当借贷人初始资产大于贷款额度时,还款强度越大,期望还清贷款所需要的时间越短。
证明:要证明T关于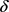 单调递减,即证明
单调递减,即证明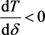 。由(18)式,
。由(18)式,
 (19)
(19)
不妨令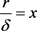 ,
, ,则有
,则有
 (20)
(20)
因为 ,所以
,所以 ,
, ,此时有
,此时有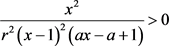 ,令
,令
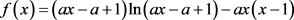 (21)
(21)
故只需要证明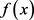 在定义域内的最大值小于零。计算可得
在定义域内的最大值小于零。计算可得
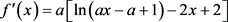 (22)
(22)
 (23)
(23)
令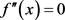 ,可得
,可得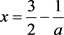 。通过分析可得,存在唯一一点
。通过分析可得,存在唯一一点 ,使得
,使得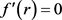 ,且当
,且当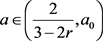 时,
时, ;当
;当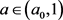 时,
时,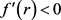 。
。
当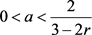 时,对
时,对 的符号进行分析,可得表3。
的符号进行分析,可得表3。
由表3可得,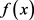 在定义域内的最大值小于零。且当
在定义域内的最大值小于零。且当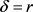 时,
时,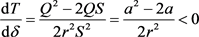 ,因此,当
,因此,当 时,
时, ,即T关于
,即T关于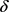 单调递减。
单调递减。
当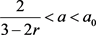 时,经分析可得表4。
时,经分析可得表4。
由表4可得, 在定义域内的值恒小于零。且当
在定义域内的值恒小于零。且当 时,
时, ,因此,当
,因此,当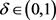 时,
时,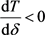 ,即T关于
,即T关于 单调递减。
单调递减。
当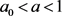 时,同理可证明当
时,同理可证明当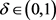 时,
时,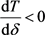 ,即T关于
,即T关于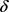 单调递减。
单调递减。
综上即证明了当固定参数S,Q,r,且 时,T关于
时,T关于 单调递减。
单调递减。
命题4.4:当固定参数S,Q,r,且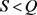 时,T关于
时,T关于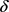 先减后增,此时存在某一
先减后增,此时存在某一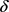 使得T有最小值。
使得T有最小值。
证明:要证明T关于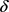 的单调性,即对
的单调性,即对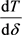 的符号进行分析。仿照命题4.3的证明,令
的符号进行分析。仿照命题4.3的证明,令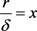 ,
, ,
,
由(20)式可得
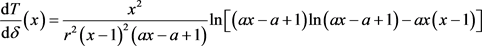 (24)
(24)
因为 ,所以
,所以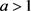 ,
,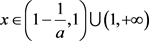 ,此时有
,此时有 ,仍令
,仍令
 (25)
(25)
故只需要证明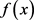 在定义域内的最大值小于零。由(23) (22)式,对
在定义域内的最大值小于零。由(23) (22)式,对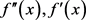 的符号进行分析。
的符号进行分析。
当 时,对
时,对 的符号进行分析,可得表5。
的符号进行分析,可得表5。
由表5的结果可将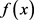 的符号统计于表6。
的符号统计于表6。
由表6可得,当 时,
时,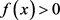 ;
; 时,
时, 。即当
。即当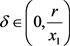 时,
时,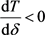 ,T关于
,T关于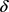 单调递减;当
单调递减;当 时,
时,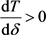 ,T关于
,T关于 单调递增;当
单调递增;当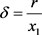 时,
时,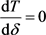 。因此,存
。因此,存
在某一 使得T有最小值。
使得T有最小值。
当 时,同理可证明存在某一
时,同理可证明存在某一 使得T有最小值。
使得T有最小值。
综上,当固定参数S,Q,r且 时,存在某一
时,存在某一 使得T有最小值。这说明当借贷人资产减少到某一域值时,由于初始时刻的资产小于贷款额度,若再增加还款强度,还款速率将大于借贷人资产的增长速率,使得借贷人最终无法还清贷款,还款期限趋于正无穷。
使得T有最小值。这说明当借贷人资产减少到某一域值时,由于初始时刻的资产小于贷款额度,若再增加还款强度,还款速率将大于借贷人资产的增长速率,使得借贷人最终无法还清贷款,还款期限趋于正无穷。
5. 数值计算与作图
经过以上的分析和计算,得到了借贷人期望还清贷款所需时间T的表达式。下面通过选取适当的参数,利用数值求解方法 [14],求解期望还清贷款时间T的数值解,并作出各个参数与T的关系图,从图中分析各个参数对T的影响。这里借贷人初始时刻资产S与贷款额度Q的单位为元,时间T的单位为年。
5.1. 时T的性质分析
时T的性质分析
图1是期望还清贷款的时间T与借贷人贷款额度Q的关系曲线。取参数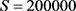 ,
, ,
, ,
, ,自变量Q的变化区间为[100000, 150000]。当固定参数S,r,q,
,自变量Q的变化区间为[100000, 150000]。当固定参数S,r,q, 时,T关于Q单调递增,见图1。这与前面参数分析的结果是一致的。在其他条件不变的情况下,借贷人的贷款额度越大,还清贷款所需要的时间就越长,这与实际是相符的。
时,T关于Q单调递增,见图1。这与前面参数分析的结果是一致的。在其他条件不变的情况下,借贷人的贷款额度越大,还清贷款所需要的时间就越长,这与实际是相符的。
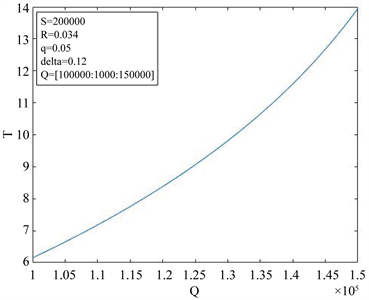
Figure 1. The influence of loan amount on loan repayment time loan repayment time
图1. 贷款额度对贷款还清时间的影响
图2是借贷人初始时刻资产S与贷款还清时间T的关系曲线。取参数 ,
, ,
,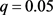 ,
, ,自变量S的变化区间为[150000, 250000],取步长为1000。当固定参数Q,r,q,
,自变量S的变化区间为[150000, 250000],取步长为1000。当固定参数Q,r,q, 时,T关于S单调递减,见图2。这与前面参数分析的结果是一致的。当还款比例一定时,借贷人资产越多,每次的还款额就越多,还清贷款所需要的时间就越短。
时,T关于S单调递减,见图2。这与前面参数分析的结果是一致的。当还款比例一定时,借贷人资产越多,每次的还款额就越多,还清贷款所需要的时间就越短。
图3是当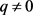 时还款强度与贷款还清时间的关系曲线。取参数
时还款强度与贷款还清时间的关系曲线。取参数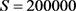 ,
, ,
, ,
, ,自变量
,自变量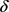 的变化区间为[0.1, 0.9],步长为0.01。当固定参数S,Q,r,q且
的变化区间为[0.1, 0.9],步长为0.01。当固定参数S,Q,r,q且 时,T关于
时,T关于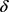 单调递减,见图3。这与前面参数分析的结果是一致的。若初始时刻的资产大于贷款额度,随着还款强度的增大,还清贷款所需要的时间就越短。
单调递减,见图3。这与前面参数分析的结果是一致的。若初始时刻的资产大于贷款额度,随着还款强度的增大,还清贷款所需要的时间就越短。
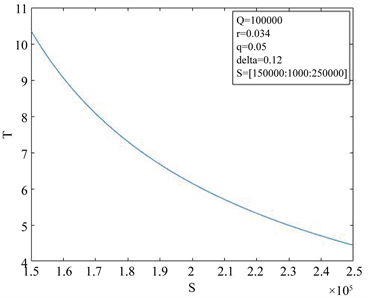
Figure 2. The influence of initial assets on loan repayment time loan repayment time
图2. 初始资产对贷款还清时间的影响
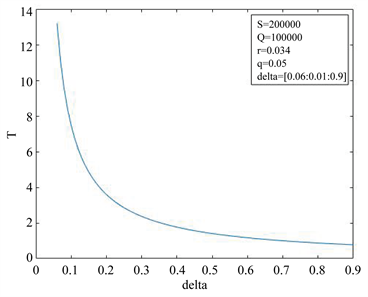
Figure 3. The influence of repayment intensity on loan repayment time on loan repayment time
图3. 还款强度对贷款还清时间的影响
图4是期望还清贷款的时间T与借贷人贷款利率q的关系曲线.取参数 ,
,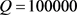 ,
,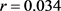 ,
, ,自变量q的变化区间为[0.035, 0.2]。当固定参数S,Q,r,
,自变量q的变化区间为[0.035, 0.2]。当固定参数S,Q,r, 时,T关于q单调递增,见图4。这与前面参数分析的结果是一致的。在其他条件不变的情况下,贷款利率越大,还清贷款所需要的时间就越长,这与实际是相符的。
时,T关于q单调递增,见图4。这与前面参数分析的结果是一致的。在其他条件不变的情况下,贷款利率越大,还清贷款所需要的时间就越长,这与实际是相符的。
5.2. q = 0时T的性质分析
图5是期望还清贷款所需时间T与借贷人贷款额度Q的关系曲线。取参数 ,
,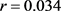 ,
, 。自变量Q的变化区间为[100000, 150000]。当固定参数S,r,
。自变量Q的变化区间为[100000, 150000]。当固定参数S,r,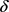 时,T关于Q单调递增,见图5。这与前面参数分析的结果是一致的。在其他条件不变的情况下,借贷人的贷款额度越大,还清贷款所需要的时间就越长,这与实际是相符的。
时,T关于Q单调递增,见图5。这与前面参数分析的结果是一致的。在其他条件不变的情况下,借贷人的贷款额度越大,还清贷款所需要的时间就越长,这与实际是相符的。
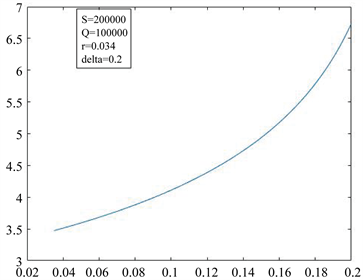
Figure 4. The influence of loan interest rate on loan repayment time on loan repayment time
图4. 贷款利率对贷款还清时间的影响
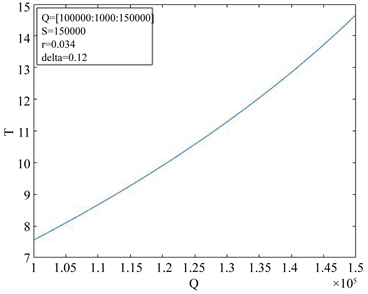
Figure 5. The influence of loan amount on loan repayment time loan repayment time
图5. 贷款额度对贷款还清时间的影响
图6是借贷人初始时刻资产S与贷款还清时间T的关系曲线。取参数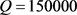 ,
,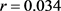 ,
,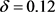 ,自变量S的变化区间为[150000, 250000],取步长为1000。当固定参数Q,r,
,自变量S的变化区间为[150000, 250000],取步长为1000。当固定参数Q,r, 时,T关于S单调递减,见图6。这与前面参数分析的结果是一致的。当还款比例一定时,借贷人资产越多,每次的还款额就越大,还清贷款所需要的时间就越短。
时,T关于S单调递减,见图6。这与前面参数分析的结果是一致的。当还款比例一定时,借贷人资产越多,每次的还款额就越大,还清贷款所需要的时间就越短。
图7是当 时还款强度与贷款还清时间的关系曲线。取参数
时还款强度与贷款还清时间的关系曲线。取参数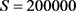 ,
,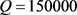 ,
,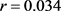 。自变量
。自变量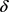 的变化区间为[0.01, 0.9],取步长为0.001。当固定参数S,Q,r且
的变化区间为[0.01, 0.9],取步长为0.001。当固定参数S,Q,r且 时,T关于
时,T关于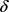 单调递减,见图7。这与前面参数分析的结果是一致的。若初始时刻的借贷人资产大于贷款额度,随着还款强度的增大,还清贷款所需要的时间就越短,这与实际也是相符的。
单调递减,见图7。这与前面参数分析的结果是一致的。若初始时刻的借贷人资产大于贷款额度,随着还款强度的增大,还清贷款所需要的时间就越短,这与实际也是相符的。
图8是当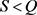 时还款强度与贷款还清时间的关系曲线。取参数
时还款强度与贷款还清时间的关系曲线。取参数 ,
, ,
,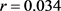 ,
,

Figure 6. The influence of initial assets on loan repayment time loan repayment time
图6. 初始资产对贷款还清时间的影响
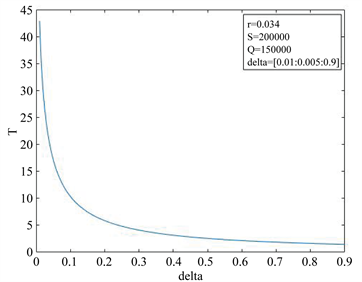
Figure 7. The influence of repayment intensity on loan repayment time when S > Q
图7. S > Q时还款强度对贷款还清时间的影响

Figure 8. The influence of repayment intensity on loan repayment time when S < Q
图8. S < Q时还款强度对贷款还清时间的影响
自变量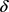 的变化区间为[0.01, 0.135],取步长为0.001。当固定参数S,Q,r且
的变化区间为[0.01, 0.135],取步长为0.001。当固定参数S,Q,r且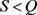 时,T关于
时,T关于 先减后增,见图8。这与前面参数分析的结果是一致的。若初始时刻借贷人资产小于贷款额度,则当借贷人资产减少到某一域值时,再增加还款强度,会导致还款速率大于资产的增长速率,使得借贷人最终无法还清贷款,还款期限趋于无穷。此时,存在某一
先减后增,见图8。这与前面参数分析的结果是一致的。若初始时刻借贷人资产小于贷款额度,则当借贷人资产减少到某一域值时,再增加还款强度,会导致还款速率大于资产的增长速率,使得借贷人最终无法还清贷款,还款期限趋于无穷。此时,存在某一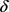 使得T有最小值,这与实际是相符的。
使得T有最小值,这与实际是相符的。
6. 总结
在本文中,针对一类具有随机性的资产或收益的借贷人,我们设计了一种新的贷款还款方式,该贷款的还款强度依赖于借贷人的资产变动,带来了还清贷款所需时间的不确定性。对于这类贷款的价值,我们建立了数学模型,得到了剩余贷款的期望价值和期望还清贷款所需时间的表达式。
期望还清贷款所需时间与贷款额度,借贷人初始资产,贷款利率,无风险利率以及还款强度有关。贷款额度越大,期望还清贷款所需的时间越长;初始时刻借贷人资产越多,期望还清贷款所需的时间越短;贷款利率越高,期望还清贷款所需的时间越长;无风险利率越高,期望还清贷款所需的时间越短;期望还清贷款所需时间与还款强度的关系则需要分情况讨论,当初始资产大于贷款额度时,还款强度越大,期望还清贷款所需要的时间越短;当初始资产小于贷款额度时,存在一种还款方式,使还清贷款所需要的时间最短。结果如表7:

Table 7. T relationship with parameters
表7. T与各参数的关系
最后进行了数值求解与作图,从图中分析了各个参数对期望还清贷款所需时间的影响。
基金项目
国家自然科学基金(11671301)。