1. 引言
计算机视觉系统在雾霾天气进行工作时,由于空气中的颗粒导致光线散射,颗粒对光线的吸收导致光线的衰减,大量信息丢失,使得系统不能正常的工作。这也使图像处理算法无法正常的处理,因此对雾天图像清晰化和减少设备对环境的依赖具有较高的研究意义。
对于雾天清晰化处理的图像去雾方法主要可分为以下两类:一类是对图像进行增强:包括全局、局部化增强。这两种增强都是基于直方图均衡化算法:将图中像素总个数少的像素进行灰度压缩,使图像中像素总个数多的灰度进行拉宽,再把这种非线性拉伸后的灰度级通过直方图均匀分布以达到去雾的效果 [1]。一类是图像复原:包括偏微分方程方法,先验信息方法,深度关系方法。先验信息方法研究人员取得了很好的成果 [2] [3] [4],包括Tan等通过基于晴朗天气下和有雾天气下大气光的变化基于目标和视觉系统的距离建立物理模型,提高有雾图像的局部对比度,在一定程度上达到将有雾图像恢复到原图像 [5]。Fattal等假定约束条件为:透射率和表面投影与介质局部统计无关,利用独立成分分析和马尔可夫随机场进行图像复原 [6] [7]。He等是对户外无雾图像大量的研究与统计,提出了暗通道算法达到去雾效果,即这些图像都会存在一些像素值很低的像素,取得了很好的去雾效果,但图像中有大面积明亮区域时得到的大气光强度A不准确导致恢复图像有问题 [8]。
本文研究基于先验信息方法中He提出的暗原色先验原理进行改进。提出对天空区域进行割据的算法:基于最大类间方差法进行形态学膨胀的改进对天空区域和非天空区域准确分割,然后对不同区域采用不同的方法获取大气光强度A,通过导向滤波算法获取细化的透射率,最后采用融合方式将处理后的天空域与非天空域进行白边消除。
2. 基于暗原色先验模型
2.1. 大气散射函数
不同的物体对光的反射能力具有不同的特性,与光在不同的介质穿过时散射作用也会增加 [9] [10],描述有雾环境下图像的物理模型应该包括两个方面:1. 光的衰减项,2. 光透过大气的散射。衰减公式为:
(式1-1)
其中d表示场景深度,
表示光强度,
表示光衰减项,
表示大气的散射系数。
散射公式为:
(式1-2)
其中
表示大气增强项,
表示原始大气光的总强度。
所以有雾环境下图像的物理模型为:
(式1-5)
将式1-1,式1-2带入得:
(式1-6)
令
,
,
,
式得
(式1-7)
这就是在机器视觉以及计算机图像处理领域的常用方程 [11]。其中,
表示有雾的待处理图像,
表示无雾的目标图像,A表示大气光强度;
表示透射率。去雾简单地说就是从
来推算出
。从式1-7看出若假设估计出A和t,代入便可得到
即去雾图像。
2.2. 暗原色先验原理
He等 [8] 基于对无雾图像的大量统计发现对于绝大多数非天空区域,至少存在一个颜色通道值很低的像素,且接近于0。提出暗通道先验模型,对于任何一个无雾图像J可以表示为:
(式1-8)
其中,
表示表示彩色图像J的各个色彩(RGB)通道,
表示以x为中心的局部窗口邻域。且
接近于0。
这里假定大气光强度A已知,且在窗口邻域内的透射率
为某一固定值。则公式1-8可以变形为:
(式1-9)
对式1-9最小化得:
(式1-10)
即:
(式1-11)
由于
接近于0即
所以式1-11得:
(式1-12)
其中为保留图像深度感,有必要保留一定程度的雾,w系数为
,一般值为0.95。
此时I、A和t都已知,即可求出J。公式为:
(式1-13)
从式1-13看出当
太小式,导致无雾图像J偏大所以
将设置下限为
(程序中值取0.1)最终获取无雾图像公式为:
。 (式1-14)
3. 改进的去雾方法
3.1. 透射率的获取
采用He提出的导向滤波算法对粗透射率再次细化处理获取 [12] :将要处理的带雾图像作为引导图,先对透射率进行粗估计滤波处理,获取细节信息,以此再次优化透射率图来获取更好的去雾效果。
导向滤波模型公式:
(式2-1)
其中p,q为输入图像与输出图像,i,j代表像素的坐标位置,I是改滤波的引导图,
是滤波核。
假设该滤波输出与引导图像为线性变化即:
(式2-2)
其中
为局部窗口邻域,k为像素中心。
是一对线性系数,若输入输出图像的差异最低则满足:
(式2-3)
其中
是正则化参数,
得到滤波结果:
(式2-5)
该滤波核系数为:
(式2-6)
其中
是引导图,
为
在
窗口的方差,
在
窗口的均值为
,
窗口中的像素数目为
。
程序首先获取原估计透射率,将获取的原估计透射率作为引导图,利用导向滤波在此细化获取更加准确的透射率,最后将小于
下限的用
代替。
3.2. 获取最优分割阈值及改进
这里基于图像的灰度直方图分类,将图像分为远景与背景,以类间的最大或类内的最小方差作为阈值的选取准则 [13] [14],按照阈值对图像进行割据。
假定某副图像的灰度级为(
),处在灰度级为i的像素点总个数为
,像素点的总个数为N,
故
。同时灰度级为i在图中出现的概率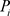 ,则满足
,则满足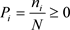 ,
, 。按照阈
。按照阈
值k对图像进行分类则有:
 ,
,
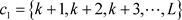 。
。
这时两类灰度出现的概率为:
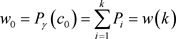 (式2-7)
(式2-7)
 (式2-8)
(式2-8)
两类的灰度平均值为:
 (式2-9)
(式2-9)
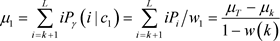 (式2-10)
(式2-10)
其中 ,
, 。对于任意k都有
。对于任意k都有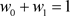 ,
, 。
。
两类的灰度方差:
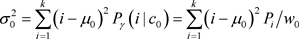 (式2-11)
(式2-11)
 (式2-12)
(式2-12)
令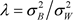 ,
, ,
, 。分别表示总体,类内,类间方差。即:
。分别表示总体,类内,类间方差。即:
 (式2-12)
(式2-12)
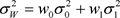 (式2-13)
(式2-13)
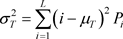 (式2-14)
(式2-14)
选取最优阈值k使得三个判定函数最大。由于 时有:
时有:
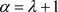 (式2-15)
(式2-15)
 (式2-16)
(式2-16)
上面可以看出 ,
, ,
, 单调性一致,又因为图像的总体方差为常量,与
单调性一致,又因为图像的总体方差为常量,与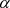 无关,所以选择最简单的
无关,所以选择最简单的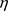 最为判定函数可得:
最为判定函数可得:
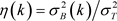 (式2-18)
(式2-18)
用类间方差作为分类性能的高低函数为:
 (式2-19)
(式2-19)
得出最佳阈值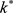 满足:
满足:
 (式2-20)
(式2-20)
计算出最优分割阈值后对图像进行分割。避免交界处噪声对分割的影响,采用多次形态学膨胀操作,获得二值图像,从中提取出天空区域和非天空区域来对单一分割进行改进。具体方法为:
循环将上面分割的结果用最大值替代卷积求和,用加法替代卷积的乘积即 [15] :
 (式2-21)
(式2-21)
其中, 表示图像f的定义域,
表示图像f的定义域, 表示结构元素b的定义域,
表示结构元素b的定义域, 都应满足图像f的定义域,
都应满足图像f的定义域, 应满足结构元素
应满足结构元素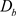 的定义域内。当最小值大于0是将值赋值为1,其他为0,进行多次循环。程序中结构元素b为3 × 3零矩阵,进行多次循环。
的定义域内。当最小值大于0是将值赋值为1,其他为0,进行多次循环。程序中结构元素b为3 × 3零矩阵,进行多次循环。
然后再将膨胀后的图像与有雾图像叠加运算,再将此时的天空区域按照式2-22判断:
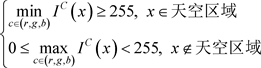 (式2-22)
(式2-22)
程序中将满足条件的天空取0,非天空区域的置1,最后得到准确分割后的天空区域与非天空区域。
3.3. 大气强度A的获取
根据He提出的算法,对暗通道图的亮度值进行排序,取最大亮度值得前0.1%的像素,将这些像素在有雾的原始图像中的最大值作为A。避免A值受到白色亮点影响A的计算结果,采用以下算法:
1. 非天空区域:统计非天空区域最大亮度的1%像素的平均值为大气光强度A的值 [16]。
2. 天空区域:将有雾图像按上述分割后天空区域均匀分成四块区域,计算平均值和标准值的最大差值与设定的阈值比较,大于阈值的继续均分成四块计算平均值和标准值的差值,当小于设定阈值时,计算选定区域的平均亮度值作为大气光强度的A值。
3.4. 优化白边效应
为了消除拼接后的分界处的白边效应公式为:
 (式2-23)
(式2-23)
其中 是按照上述非天空区域大气光强度进行暗原色先验处理后的图像,将天空区域设置0,
是按照上述非天空区域大气光强度进行暗原色先验处理后的图像,将天空区域设置0,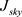 是经过上述改进后处理的天空区域,非天空区域设置成0,最后获取
是经过上述改进后处理的天空区域,非天空区域设置成0,最后获取 为去雾图像。
为去雾图像。
4. 试验结果与分析
试验运行环境为win10家庭版,matlab版本为2014b,图像为选取带雾图片。
最大类间方差法进行单一阈值分割与阈值分割进行形态膨胀改进后的阈值分割图像对比,分割处理后的天空区域与非天空区域结果为图1。从图1的试验结果看出本文改进的阈值分割能够很好的分割出天空域与非天空域,验证了本文对阈值分割算法的改进。基于导向滤波的改进获取透射率结果为图2。从图2看出基于导向滤波改进后来获取的透射率更加细化,更符合实际。最后原图像与去雾后的图像对比结果为图3,试验图3结果表明还原后的图像在雾浓度较小时能够达到良好的去雾效果且对于天空区域没有明显的色块,去雾后图像更加自然清晰。

Figure 1. Single threshold segmentation and improved threshold segmentation
图1. 单一阈值分割与改进后阈值分割

Figure 2. Original transmittance and improved transmittance
图2. 原透射率与改进后的透射率

Figure 3. Original image and image after defogging
图3. 原图像与去雾后的图像
5. 结语
通过对暗原色先验不适合用于天空域的去雾处理研究与分析,提出对天空区域进行割据的去雾算法:以最大类间方差法算法进行阈值分割图像,然后对其进行形态学膨胀处理,改进膨胀算法,能够更有效的分割出天空区域。通过对研究导向滤波,获取更加细致的透射率并提出给其设置下限使得复原的图像误差更低。但试验结果中选取图像中雾的浓度较大时,复原的图像出现日晕现象,复原图像效果不理想,这也是进一步研究的内容。