1. 引言
本文考虑如下玻尔兹曼方程的不可压缩极限:
,
,
,
, (1)
.
其中
是
上有界区域,
,
,
,
。定义
,
。
表示给定的外力,F是稀薄
气体分子的分布函数,
表示气体分子的平均自由程。
文献 [2] [3] 在一些先验假设下研究了玻尔兹曼方程的不可压缩的Navier-Stokes-Fourier (简称INFS)极限。对于重整化解的收敛极限,完整证明由 [4] 给出。对于稳态Boltzmann的研究则比较少,正如文献 [5] 所指出,尽管稳态Navier-Stokes-Fourier方程在应用中很重要,但从稳态Boltzmann推导出稳态Navier-Stokes-Fourier方程一直是一个待解决的重要问题。最近文献 [6] 通过L2-L∞方法结合L6估计证明了三维稳态玻尔兹曼方程的不可压缩极限。在此基础上我们研究二维稳态玻尔兹曼方程的不可压缩极限。需要指出,相比于三维情形,对于二维稳态玻尔兹曼方程,我们需要L2-L∞方法结合新的L4估计来研究,由此导致了不同估计和困难。
本文主要结果如下:
定理1.1:设
是
中的有界开集,边界
属于
,若
,且
,则
对于
,(1)存在唯一解
,f满足
,在
上,
,在
上,
并且
,
其中
,
,
。
最后,当
,f在
上弱收敛于
,而
是具有狄利克雷边界条件以及外力场
的稳态INFS方程的唯一弱解:
,
,在
上,
,在
上,
,在
上,其中
。
2. 预备知识和主要引理
首先引进一些基本记号:
我们定义下列范数:
;
,
;
表示
范数或者
范数;
表示
范数或者
范数。
等价于
,C是与
无关的常数;定义
。
定义2.1:记
的边界为
,我们将
分为以下三种情况:
,
,
.
定义2.2:设
是任意一点,且
,令
,我们有如下定义:
,
,
其中,对于
,
,
。
引理2.3:假设
,存在
使得
, (2)
且f是下述方程在分布意义下的解:
,在
上,(3)
,在
上,
则对足够小的
以及趋于1的
,
,(4)
且
, (5)
, (6)
其中
,
。
证明:(4),(5)的证明见参考文献 [6],下面证明(6)。
令
,根据格林公式(见参考文献 [6]),得
.
结合上式以及
,由(3)得到
. (7)
令
,则
,分以下三步证明。
第一步 估计c,对于足够小的
,我们将证明如下结论:
. (8)
这里择测试函数
,其中
,
,
是一待定常数。
估计(7)的右边需要下列Sobolev-Gagliardo-Nirenberg不等式:
对于
和有界
区域
,若
,则对任意的
,有
, 并且
连续嵌入
(见文献 [7])。
当
时,我们想要
,所以由
,得
,这里我们取
,则对于任意的
,
,
因此由标准椭圆估计(见参考文献 [8]),得到
,(9)
那么
(7)的右边
。 (10)
将
代入(7),则(7)的左边可以写成如下形式:
(11)
(12)
(13)
. (14)
我们对每一项进行估计。
对f进行分解得到:
,在
上, (15)
,在
上。 (16)
取
使得
,则由奇函数性质,(13)表达式变成如下形式:
(17)
. (18)
计算可得
,则由
得
. (19)
. (20)
当
时,由(
的奇性可得
.
且当
是
上的
区域时,我们有下述估计
.
当
且
时,
。
令
,由(9)得
,所以
. (21)
由(9)以及Holder不等式可得
, (22)
其中,我们令
。
最后,将(15)代入(14),通过计算以及奇函数性质可得
. (23)
由(10),(19),(20),(21),(22),(23)得
.
第三步 估计b。我们将得到,对足够小的
,有
. (24)
我们通过估计
和
来估计b。
对固定
,为了估计
,我们选择测试函数
, (25)
其中
是一个待定常数且
。
与前面类似,将测试函数(25)代入(7)右边得
(7)右边
。 (26)
下面我们将(15)和(16)代入(7)左边,通过计算化简得到
(27)
(28)
(29)
(30)
与前面类似,
. (31)
. (32)
将(15)代入(29),由函数的奇性得
. (33)
选择
使得对
,
,计算得
(33)中第一项
, (34)
(33)中第二项
。 (35)
. (36)
由(26),(31),(32),(34),(35),(36)得,对足够小的ε,
. (37)
下面估计
,选择
。与(26)类似,
(7)右边
。
同样地,将(15),(16)代入(7)左边,由奇函数性质可知
. (38)
(38)中第一项
。
其余项估计与前面类似,所以我们得到
的估计,结合(37)得到(24)。
第四步 估计a,我们将证明对于足够小的
,
. (39)
这里选择测试函数 ,
,
其中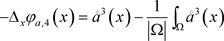 ,
, 。
。
选择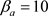 ,使得
,使得 ,则将
,则将 代入(7)右边得
代入(7)右边得
(7)右边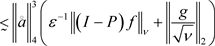 。
。
将(15),(16)代入(7)左边,包含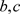 的项积分为0。对a的估计,处理方法同
的项积分为0。对a的估计,处理方法同 ,只需验证:
,只需验证:
 .
.
因为
 ,
,
所以 ,
,
从而(6)成立。证毕。
引理2.4:令f满足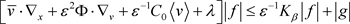 ,
,
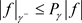 ,
,
其中 ,
, 。对于
。对于 ,
,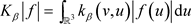 ,
,
 .
.
如果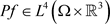 ,
, ,那么,对于
,那么,对于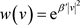 ,
, ,
,
 . (40)
. (40)
证明:要证明引理2.4,只需要证明
 . (41)
. (41)
二维区域上的变量替换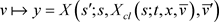 ,对于
,对于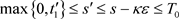 ,
,
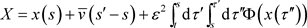 .
.
由计算可得
 .
.
由下界 ,得
,得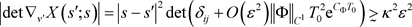 。
。
对于二维区域,由参考文献 [6] 可知,要证明(41)只需证明下面两个不等式,其他计算同三维。
 ,
,
 .
.
结论成立。证毕。
引理2.5:假设(2)仍然成立,则对于充分小的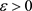 ,下式存在唯一的解,
,下式存在唯一的解,
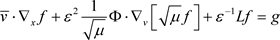 ,在
,在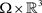 上,
上,
 ,
,
并且
 , (42)
, (42)
 . (43)
. (43)
证明:(42)的证明见参考文献 [6]。 ,所以(43)可由引理2.3的(6)得到。
,所以(43)可由引理2.3的(6)得到。
3. 定理1.1的证明
本节将给出定理1.1的证明。为此,我们定义一个范数:
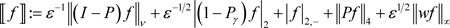 .
.
我们有如下结论。
定理3.1:假设 使得
使得
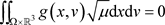 ,
,
则对于足够小的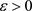 ,下式存在唯一解
,下式存在唯一解
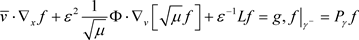 ,
,
且有
 ,
,
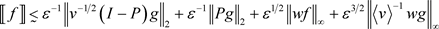 .(44)
.(44)
证明:根据引理2.5,要证定理3.1,只需要证明(44)。首先用引理2.4中的(40)估计(43)中的 ,得到对于足够小的
,得到对于足够小的 ,有
,有
 . (45)
. (45)
由(40),(42),(45)可以得到(44)。
引理3.2:对于 ,
,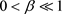 ,我们有
,我们有
 , (46)
, (46)
其中 。
。
证明:由参考文献 [6] 可以得到
 .
.
要证明(46),只需要估计最后一项,其余证明同参考文献 [6]。
由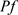 关于v的强衰减性,可以得到,对于任意的
关于v的强衰减性,可以得到,对于任意的 ,
,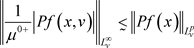 ,其中
,其中 表示
表示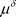 ,
, 。对于固定v,由
。对于固定v,由 ,我们有
,我们有
 .
.
由此可以得到(46)。证毕。
定理1.1的证明:根据上述结果,按照文献 [1] 的推导可得f的存在唯一性,并且它的弱极限点
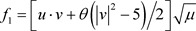 的系数
的系数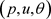 满足INSF方程和边界。由于
满足INSF方程和边界。由于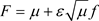 ,F的存在唯一性
,F的存在唯一性
可以直接得到。证毕。