1. 引言
高等数学课程是高等院校针对人才培养指向而开设的基础课程,内容具有一定的抽象性、概括性、缜密的逻辑性,其与现实岗位思维能力需求紧密联系,直接关系到学生的未来岗位工作能力。案例教学,是一种开放式、互动式的新型教学方式,通常要针对理论指定案例,提前指导学生阅读并组织学生开展讨论,形成反复的互动与交流,通过各种信息、知识、经验、观点的碰撞来达到启示理论和启迪思维的目的。案例教学能够最大限度地提供岗位工作的经验和感受,促进工作能力的生成和提高。因此,根据高等数学课程特点,探索案例教学的特点与规律,以及如何适应高等数学教学改革需要,是值得进一步研究和思考的。
近些年,国内很多专家教授在这方面做了大量工作。王树林(2004年)指出高校教育中存在着将事例教学等同于案例教学,以战例教学、想定教学代替案例教学等认识误区,探讨案例教学中存在的问题,找到解决良策,对积极推进现代教学深入发展,具有重要的意义 [1]。杨宗佑和李彦明强调要深入研究高校案例教学,必须坚持以培养决策能力为主,与其他方法紧密结合,扎实抓好应用案例教材编写和提高教员案例教学能力 [2]。王森华等阐述了如何将计算思维引入应用案例设计中,并根据程序设计中的抽象模型解决复杂现实问题,将计算机程序设计课程引入到应用案例分析中 [3]。
基于上述研究,本文通过分析高等数学案例教学实施现状,提出了构建新型案例教学模式的方式方法,并且以实际教学案例进行分析。
2. 高等数学案例教学实施现状
高等数学是高校学生入学后的第一门数学课程,是众多基础课、专业基础课及专业课的先行课程,是学生掌握数学工具,提高数学素养的主要课程。然而,在目前的高等数学教学过程中,案例教学往往没能引起足够的重视。在高等数学的案例教学过程中,主要存在着以下问题:
(1) 高等数学案例教材缺乏针对性
高等数学课程多选择知名大学编写的经典教材,其编排一般按照“定义–定理–证明–习题”的顺序,课程内容侧重于理论推导证明和知识的系统完整,涉及高等数学理论知识在实际中应用的内容很少。针对各知识点,目前还没有可应用的针对性强和教学可操作性强的案例教材,解决实际问题的数学实验也不多,能够展示数学建模过程,达到理论与实际相结合的教材更是凤毛麟角。
(2) 高等数学案例教学未列入高等数学教学计划
高等数学案例教学必须有一定的教学条件来支持。将案例教学列入高等数学教学计划,并作为高等数学教学的一个重要环节,专门安排课时进行教学并开展教学检查,是考核评价高等数学案例教学实施成效的重要前提和手段 [4]。从目前情况来看,大多数高校并未把案例教学的课时安排和教学检查考核列入高等数学的教学计划中,只是在个别课程的教学中,要求讲解案例。
(3) 高等数学教师在案例教学能力方面未达到一定高度
案例教学是一种交互式的探索过程,虽然我们强调“主角”是学生,以学生为中心,但“配角”——教师的指点、引导作用是不可低估的,这也是决定高等数学案例教学成败的关键。教师须把案例教学引向深入,从而达到培养学生思考问题、分析解决实际问题能力的效果。目前,虽然大多数高等数学教师理论水平较高,但由于接触相关实际问题少,不能将高等数学理论与实际问题相结合,这是很难保证教学质量的。
基于以上现状,在高等数学教学改革如火如荼的当下,对于案例教学模式的改进也迫在眉睫。
3. 构建案例教学在高等数学教学中的新模式
针对高等数学案例教学存在的主要问题,要使高等数学案例教学在高校素质教育中真正发挥作用,应主要采取以下措施。
(1) 通过数学发展史、数学建模和调研充实案例库
高等数学是一门产生于实际应用的学科,其每一个概念都是为了解决一类问题而产生的,而这一类问题就是进行案例教学的素材;同时,每年举行的数学建模竞赛题目本身就是案例,其往往来源于目前比较热门的实际问题。这些素材恰好弥补了现有高等数学案例教材针对性不强的缺陷。另外,还应鼓励教师进行走访和调研,搜集相关教学案例,将高等数学的教学内容与学生的实际专业背景和工程情景联系起来。将高等数学的教学内容与数学发展史、数学建模和调研成果相互融合,有助于丰富学生的学习内容,吸引学生在课堂上的注意力,提高课堂的学习效率。以此同时,通过调研和建模竞赛辅导,高等数学教师的案例储备量也得到提升,进而案例教学水平也得到相应提高。
(2) 将案例教学引入高等数学日常教学计划
高等数学课程内容多且课时量有限,需要将应用案例适时的引入章节讲授过程中。比如,在习题课讲解时对该章节涉及应用案例进行具体讲解。课前将具体的案例问题发送给学生,安排学生了解和搜集相关资料,让学生带着问题参与到教学中。在课中教员以“为什么–是什么–怎么办”为主线,通过简述相关理论知识,引导学生利用数学理论去解决应用案例中的问题 [5]。在课后学生可以总结相关基础理论和相关应用案例,逐步提升实际应用能力,并且提高应用案例教学中的论文或作业在学生综合考核成绩中的比例。通过课前、课中和课后三阶段的教学任务安排,提高学生运用高等数学知识分析应用案例并解决相关问题的实际应用能力。
(3) 借助数学软件实施高等数学案例教学
利用Matlab、Mathematica、Python和SPSS等现代数学软件工具,将应用案例与高等数学教学相结合,已成为教学改革的趋势。利用数学软件强大的图像和数据处理功能,通过直观图形、动画演示进行理论验证与数据分析,使得应用案例和高等数学的教学课程更生动、直观、形象,也将抽象复杂的概念形象化、简单化,弥补传统教学直接讲授的抽象与乏味,提高学生的兴趣。此外,还能更好地促进师生之间的互动,改善传统教学的弊端,同时提高学生的数学软件应用能力。
(4) 合理组建安排学习小组
按照“组间同质、组内异质”的原则组建各学习小组是教员参与、指导学生的学习过程,也是促进学生合作学习顺利开展的基础。可以各学生队小班为单位组建,明确“应用案例学习”的目标和责任分工,根据案例教学的任务和主题,留给学生充足的自主探索空间,在独立思考的基础上进行,与自主探索有机结合,尤其是高等数学中的教学重点、难点、疑点问题或发展性、开放性、研究性的问题,可以安排小组学习。这样可以适度调整训练点,富有挑战性,易激发学生的求知欲,帮助学生提高合作技巧,顺利完成学习任务。
通过融合数学史、数学软件和建模竞赛辅导等建立的案例教学新模式,可以逐步提升高等数学教师的案例教学能力,拓展学生的视野,提升数学软件应用能力,进一步推动高等数学的教学改革。
4. 案例:从追踪信号源问题到傅里叶级数
信号追踪过程中有诸多追击问题,当追击者追踪一个运动的信号源时,需要不断地改变其搜索方向,因此会在平面内形成一个折线路径图。假定其按照相邻两折线间等夹角,且每一步长是前一步长一半的规律,如何判断追击者最终能否逮住这个运动信号源,并且确定最终逮住这个运动信号源的位置,是一个值得研究的问题。
求解该问题的主要思路是利用高等数学的级数理论构建动态关系进行求解。案例教学在高等数学课程中的探索和实践过程,包括问题描述、问题分析、问题求解、归纳总结以及结果评价等部分,在此,从课前、课中和课后三个阶段来具体分析该问题。
(1) 课前准备
安排学生查阅相关案例和背景资料,以及所涉及相关理论知识及其发展史,初步分析该案例所涉及的知识点。教师在此指出两个关键问题:如何用傅里叶级数描述该问题,并且验证傅里叶级数的敛散性。为了辅助学生,教师简单讲解追击者的路径:从坐标原点
(记为
)走到
,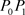 与x轴正向夹角为
与x轴正向夹角为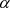 ,
,
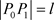 ,再从点
,再从点 走到
走到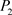 ,
, 与
与 夹角也为
夹角也为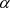 ,但
,但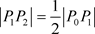 ,又从点
,又从点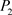 走到点
走到点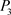 ,
,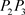 与
与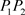 夹角为
夹角为 ,但
,但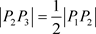 ,……按此规律一直追踪下去,结合图形得出各向量的数学表达,从而终点
,……按此规律一直追踪下去,结合图形得出各向量的数学表达,从而终点
向量表示为傅里叶级数。
(2) 课中讲解
复习傅里叶级数理论知识和相关公式,提出该应用案例的问题实质就是证明该傅里叶级数是收敛的,并求其前n项的和。将现实问题转化为纯数学模型,利用向量的复数形式和欧拉公式进行求解。讲解过程借助PPT进行相关视频演示,在黑板上板书分析问题的过程。
具体过程如下:首先,假设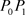 和x轴正向夹角为
和x轴正向夹角为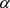 ,
,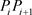 与
与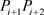 间的夹角为
间的夹角为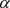 ,
, ,
, ,……,
,……,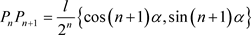 ,……,
,……,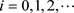 ,因此,
,因此,

接着,判断P点的坐标。上述右端的向量级数等价于复数项级数,即 。这是一个以
。这是一个以 为公比的等比级数,由于
为公比的等比级数,由于 ,所以该级数是收敛的,根据等比级数求和公式,得到
,所以该级数是收敛的,根据等比级数求和公式,得到
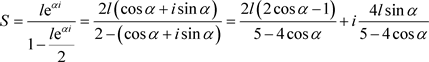
所求点坐标为
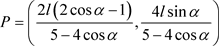
最后,通过Matlab软件,向学生展示该模型的程序,并且通过相关参数的选取,演示具体计算过程。从图1和图2可知,追击者跟踪该运动信号源,并且该信号源随着夹角和步长收敛于一个固定点,进一步可以确定该运动信号源的运动轨迹和具体位置。

Figure 1. The variation tendency of X axis and Y axis of point P with the change of angle α and step size l
图1. 点P的横坐标和纵坐标随着夹角α和步长l的变化趋势
(3) 课后安排
根据应用案例的具体讲解,学生需要总结傅里叶级数展开、收敛和求和等具体知识,练习相关数学软件的编程和命令,并且进一步查阅傅里叶级数的产生及发展历史拓展视野,完成最终的学习报告。
通过该案例的课程设计和讲解,使学生体会到高等数学的知识点来源于实际问题,并能够利用理论知识初步解决相关问题,进而提高学生学习高等数学的兴趣和学以致用的能力。
5. 总结
教学实践表明,案例教学模式改变了“概念–定理–证明–习题”的灌输式教学模式,将数学软件融入教学,能够解决“实际–问题–数学”的应用意识和能力的培养 [6]。本文根据案例教学的定义和必要性,通过分析现状,提出了融合数学软件和改革教学内容的新模式,具体通过构建高等数学教学内容、数学建模和数学史相结合,应用案例进课堂,数学软件架桥梁,的确可以达到提高学生学习兴趣,激发学生学习的自觉性、主动性,提高观察问题、分析问题、解决问题的能力。