一种基于标签比例信息的迁移学习算法

A Label Proportion Information-Based Transfer Learning Algorithm

摘要: 标签比例学习问题是一项仅使用样本标签比例信息去构建分类模型的挖掘任务，由于训练样本不充分，现有方法将该问题视为单一任务，在文本分类中的表现并不理想。考虑到迁移学习在一定程度上能解决训练数据不充分的问题，于是如何利用历史数据(原任务数据)帮助新产生的数据(目标任务数据)进行分类显得异常重要。本文提出了一种基于标签比例信息的迁移学习算法，将知识从原任务迁移到目标任务，帮助目标任务更好构建分类器。为了获得迁移学习模型，该方法将原始优化问题转换为凸优化问题，然后解决对偶优化问题为目标任务建立准确的分类器。实验结果表明，大部分条件下所提算法性能优于传统方法。

Abstract: The learning with label proportions problem is a learning task that only uses bag’s label propor-tions information to build a classification model. Due to insufficient training samples, the existing methods that viewed the above problem as single task did not perform well in text classification. To some extent, transfer learning can solve the problem of insufficient training data, the problem that how to use historical data (the original task data) to help the newly generated data (target task data) to classify becomes extremely important. This paper presents a label proportion information-based transfer learning approach to transfer knowledge from the source task to the target task, helping the target task to build a classifier. In order to obtain the transfer learning model, this method converted the original optimization problem into a convex optimization problem, and then solved the dual optimization problem to establish an accurate classifier for the target task. Extensive experiments have shown that the proposed method outperforms the traditional methods.

1. 引言

在传统监督学习的分类问题中，已知所有样本的标签，分类器可以通过大量样本属性及其标签学习得到，进而利用学习得到的分类器对未知标签的样本进行预测。但在实际应用中，通过人工标注获取样本标签需要较高成本，或者受限于隐私等客观条件，有时无法获取所有样本的标签，而仅仅已知各类样本的标签比例信息，比如在匿名投票中，只能知道反对票和赞成票的比例。因此，在已知样本标签比例信息的前提下，以多个样本组成的包为单位，基于包内样本和包的标签比例信息来训练从而获取样本层面的分类器，更加具有实用价值。

近年来，标签比例学习 [1] [2] (Learning with Label Proportions, LLP)在数据挖掘引起了广泛的关注，并成功应用于现实生活中的许多领域，如欺诈识别、银行重要客户识别、垃圾邮件过滤、视频事件检测、收入预测、视觉特征建模等。在标签比例学习问题中，只知道每个包中属于不同类别的样本的比例，但是样本的标签是未知的，它基于包层面的标签比例信息解决了样本层面的分类问题。

迁移学习(Transfer Learning) [3] [4] 是可以将知识从原任务(Source task)迁移到目标任务(Target task)的一种新的机器学习方法，其运用已存有的知识对不同但相关领域问题进行求解，迁移的知识可以帮助目标任务建立迁移学习分类器以进行预测。然而，大多数现有的方法都没有考虑实践中从原任务到目标任务的知识迁移，将标签比例学习视为单一任务，无法解决迁移学习问题。

综上所述，本文针对标签比例学习问题，为了训练得到更准确的分类器，提出了一种基于标签比例信息的迁移学习算法(label proportion information-based transfer learning method, LPI-TL)，该方法可以利用迁移学习将知识从原任务迁移到目标任务，帮助目标任务构建分类器。首先为了帮助目标任务学习预测模型，本文提出了一种迁移学习模型，然后使用拉格朗日方法将方法的原始问题转换为凸优化问题并求解，最后获得目标任务的预测分类器。实验结果表明，本文方法在标签比例问题上能取得更好的性能。

本文主要贡献如下：

1) 结合支持向量回归算法提出了基于标签比例信息的迁移学习模型，该模型可以利用迁移学习将知识从原任务迁移到目标任务。

2) 利用拉格朗日方法将原始目标模型转换为凸优化问题，并获得原任务和目标任务的预测模型。

3) 在多个数据集上进行广泛实验，并与现有算法进行对比，验证了提出算法的有效性。

2. 问题描述与相关工作

2.1. 问题描述

在标签比例学习问题中，一个包内含有多个样本，仅知道包中不同类别样本的标签比例信息。本文定义包的标签比例为包中正样本的比例。假设给定的原任务数据集为 $D=\left\{x_{\text{1}},x_{\text{2}},\cdots ,x_n\right\}$，则每个样本x_i所对应的标签y_i未知，数据会被分为t₁个互相独立的包 $\left(B_I^s,P_I^s\right),I=1,2,\cdots ,t_i$，其中 $B_I^s$ 和 $P_I^s$ 分别表示原任务数据集的第I个包和包中正样本的比例 $P_I^s=\left|\left\{x_i\in B_I^s:y_i=1\right\}\right|/\left|B_I^s\right|$，同理，目标任务数据集用 $\left(B_J^t,P_J^t\right),J=1,2,\cdots ,t_2$ 表示。

对于二元分类问题，标签比例学习任务是学习一个分类器将未知标签样本分为正类或负类。如图1所示：图左边的黑色椭圆表示包，黑色圆圈表示未标记的样本。在图的右边，加号“+”和减号“−”分别表示分类后的正样本和负样本，实线表示由标签比例和未标记的样本训练得到的分类器。

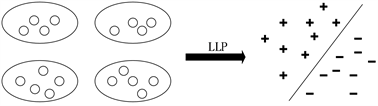
Figure 1. Two-class label proportions learning problem

图1. 二分类标签比例学习问题

2.2. 相关工作

本目前，国内外有多种标签比例学习分类方法的研究，主要分为概率模型和支持向量机模型两类。

基于概率模型的分类方法。文献 [5] 假设给定类变量的预测变量之间具有条件独立性，并采用了三种期望最大化算法来学习朴素贝叶斯模型。文献 [6] 通过估计条件类密度来估计后验概率，从贝叶斯角度提出一种新的学习框架，并且利用估计对数概率的网络模型来求解分类问题的后验概率。文献 [7] 构建了一个应用于美国总统大选的概率方法，该方法使用基数势在学习过程中对潜在变量进行推理，并引入了一种新的消息传递算法，将基数势扩展到多变量概率模型。文献 [8] 开发模型并使用Twitter数据来估算美国总统大选期间政治情绪与人口统计之间的关系。

基于支持向量机(Support Vector Machine, SVM)的分类方法。文献 [9] 提出InvCal算法，该方法可以利用样本的比例信息，反推出分类器，使得分类器预测出的样本比例与实际比例相近。文献 [10] 提出了Alter-SVM算法并通过交替优化的方法最小化损失函数。该方法在标准SVM模型的基础上加入了比例损失的约束项，使得模型得到每个包的比例与实际比例尽可能接近。在文献 [10] 的基础上，文献 [11] 提出了一种基于二支持向量机的分类模型，模型被转换为两个更小的二分类问题求解。文献 [12] 首先分析了比例学习问题中的结构化信息，并利用数据点的几何信息引入拉普拉斯项并且讨论了如何将比例学习框架与拉普拉斯项结合。文献 [13] 提出了一种基于非平行支持向量机的解决方案并将分类器改进为一对非平行分类超平面。

尽管对标签比例学习的研究已经比较深入，然而大部分研究仅将该问题视为单一任务，没有利用历史数据弥补训练样本不充分的不足，不能很好地体现出分类器的效果。不同于大部分已有的工作，本文从迁移学习角度出发，利用迁移学习可以在相似领域中帮助新领域目标任务学习的特性，提出了一种基于标签比例信息的迁移学习方法，该方法基于支持向量回归方法并结合样本组成的包构建模型，并给出了目标方程从而解决了迁移学习方法运用于标签比例学习分类的问题。

3. 标签比例学习算法

由于只通过标签比例信息无法直接训练分类函数，参考InvCal [9] 中利用标签比例信息反推出分类器的操作，提出的方法使用Platt尺度函数 [14] 并反解求出y：

$y=-\log \left(\frac{1}{p}-1\right)$ (1)

则每个包预测的y值可表示为：

${\forall }_i:\frac{1}{\left|B_i\right|}{\displaystyle \underset{j\in B_i}{\sum }\left(w^{\text{T}}{x}_j+b\right)}=y_i$。 (2)

3.1. 目标函数

除对于具有相关性的原任务数据集和目标任务数据集，该算法使用f₁和f₂分别表示原任务和目标任务分类器：

$f_1\left(x\right)=w_1^{\text{T}}\cdot x+b_1$ (3)

$f_2\left(x\right)=w_2^{\text{T}}\cdot x+b_2$ (4)

其中 $w_{\text{1}}=w_0+v_{\text{1}}$， $w_{\text{2}}=w_0+v_{\text{2}}$，w₀表示分离超平面的权向量公共参数，v₁和v₂为增量参数，原任务和目标任务越相似，则v₁和v₂越“小”，b₁和b₂是偏差。

本文对每个包中所有样本求平均值得到一个平均数样本来代表包，并利用支持向量回归算法对所得到的平均数样本求回归方程，于是LLP问题转换为求解如下目标函数：

$\min \frac{1}{2}{\Vert w_0\Vert }^2+\frac{{\lambda }_1}{2}{\Vert v_1\Vert }^2+\frac{{\lambda }_2}{2}{\Vert v_2\Vert }^2+C_1{\displaystyle \underset{i=1}{\overset{t_1}{\sum }}\left({\xi }_{1i}+{\xi }_{1i}^{*}\right)}+C_2{\displaystyle \underset{m=1}{\overset{t_2}{\sum }}\left({\xi }_{2m}+{\xi }_{2m}^{*}\right)}$ (5)

约束条件：

${\forall }_{i=1}^{t_1}:\begin{array}{l}\frac{1}{\left|B_i^s\right|}{\displaystyle \underset{j\in B_i^s}{\sum }\left(w_1^{\text{T}}{x}_j+b_1\right)}-y_i\le {\epsilon }_{1i}+{\xi }_{1i}\hfill \\ y_i-\frac{1}{\left|B_i^s\right|}{\displaystyle \underset{j\in B_i^s}{\sum }\left(w_1^{\text{T}}{x}_j+b_1\right)}\le {\epsilon }_{1i}+{\xi }_{1i}^{*}\hfill \end{array}$

${\forall }_{m=1}^{t_2}:\begin{array}{l}\frac{1}{\left|B_m^t\right|}{\displaystyle \underset{n\in B_m^t}{\sum }{\displaystyle \underset{n\in B_m^t}{\sum }\left(w_2^{\text{T}}{x}_n+b_2\right)}}-y_m\le {\epsilon }_{2m}+{\xi }_{2m}\hfill \\ y_m-\frac{1}{\left|B_m^t\right|}{\displaystyle \underset{n\in B_m^t}{\sum }\left(w_2^{\text{T}}{x}_n+b_2\right)}\le {\epsilon }_{2m}+{\xi }_{2m}^{*}\hfill \end{array}$

${\xi }_{1n},{\xi }_{1n}^{*}\ge 0\left(n=1,\cdots ,t_1\right)$

${\xi }_{2m},{\xi }_{2m}^{*}\ge 0\left(m=1,\cdots ,t_2\right)$

其中： ${\xi }_{ti}$ 和 ${\xi }_{ti}^{\ast }\left(t=1,2\right)$ 为训练误差， ${\epsilon }_{1i}$ 和 ${\epsilon }_{2m}$ 为可容忍损失，控制 $\epsilon$ 损失带的大小；参数 ${\lambda }_1$ 和 ${\lambda }_2$ 用来控制原任务和目标任务权重，C₁和C₂是边缘与经验损失的权衡参数。

为了更好地理解迁移学习，图2示意了知识迁移的基本思想。图2中圆圈表示样本，圆圈内数字表示样本所属包的编号，每个包都有两个未知标签的样本，只知道包中正样本的比例为50%；实线和虚线则分别表示分类器和间隔边界。在图的右边，红色圆圈表示目标任务样本，当仅利用目标任务样本构建分类。

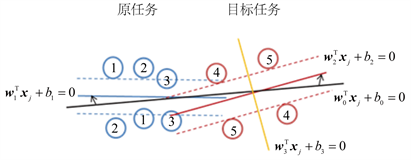
Figure 2. Transfer knowledge from the source task to the target task

图2. 原任务迁移知识到目标任务

3.2. 对偶问题

由于目标函数公式5为凸函数，引入拉格朗日乘子，公式5转换为其对偶问题，等同为最小化下式：

$\begin{array}{l}\frac{1+{\lambda }_1}{2{\lambda }_1}{\displaystyle \underset{i,j=1}{\overset{t_1}{\sum }}\frac{\left({\alpha }_{1i}^{*}-{\alpha }_{1i}\right)\left({\alpha }_{1j}^{*}-{\alpha }_{1j}\right)}{\left|B_i^s\right|\left|B_j^s\right|}}K\left(x_i,x_j\right)\\ +\frac{1+{\lambda }_2}{2{\lambda }_2}{\displaystyle \underset{m,n=1}{\overset{t_2}{\sum }}\frac{\left({\alpha }_{2m}^{*}-{\alpha }_{2m}\right)\left({\alpha }_{2n}^{*}-{\alpha }_{2n}\right)}{\left|B_m^t\right|\left|B_n^t\right|}}K\left(x_m,x_n\right)\\ +{\displaystyle \underset{i=1}{\overset{t_1}{\sum }}{\displaystyle \underset{m=1}{\overset{t_2}{\sum }}\frac{\left({\alpha }_{1i}^{*}-{\alpha }_{1i}\right)\left({\alpha }_{2m}^{*}-{\alpha }_{2m}\right)}{\left|B_i^s\right|\left|B_m^t\right|}}}K\left(x_i,x_m\right)\\ -{\displaystyle \underset{i=1}{\overset{t_1}{\sum }}\left(y_i\left({\alpha }_{1i}^{*}-{\alpha }_{1i}\right)-{\epsilon }_{1i}\left({\alpha }_{1i}^{*}+{\alpha }_{1i}\right)\right)}\\ -{\displaystyle \underset{m=1}{\overset{t_2}{\sum }}\left(y_m\left({\alpha }_{2m}^{*}-{\alpha }_{2m}\right)-{\epsilon }_{2m}\left({\alpha }_{2m}^{*}+{\alpha }_{2m}\right)\right)}\end{array}$ (6)

约束条件：

$\underset{i=1}{\overset{t_1}{{\displaystyle \sum }}}\left(a_{1i}-a_{1i}^{*}\right)+\underset{m=1}{\overset{t_2}{{\displaystyle \sum }}}\left(a_{2m}-a_{2m}^{*}\right)=0$

${\forall }_{i=1}^{t_1}:0\le {\alpha }_{1i},{\alpha }_{1i}^{*}\le C_1$

${\forall }_{m=1}^{t_2}:0\le {\alpha }_{2m},{\alpha }_{2m}^{*}\le C_2$

其中K是核函数， $\alpha =\left[{\alpha }_{1i},{\alpha }_{1i}^{*},a_{2m},a_{2m}^{*}\right]\ge 0$ 为拉格朗日乘子。公式6为凸函数可用现有方法直接求解出拉格朗日乘子a，则目标任务分类器中w₀和v₂可通过下式求得：

$w_0=\underset{i=1}{\overset{t_1}{{\displaystyle \sum }}}\left(a_{1i}^{*}-a_{1i}\right)\frac{1}{\left|B_i^s\right|}\underset{j\in B_i^s}{\overset{}{{\displaystyle \sum }}}{x}_j+\underset{m=1}{\overset{t_2}{{\displaystyle \sum }}}\left(a_{2m}^{*}-a_{2m}\right)\frac{1}{\left|B_m^t\right|}\underset{j\in B_m^t}{\overset{}{{\displaystyle \sum }}}{x}_n$ (7)

$v_1=\frac{1}{{\lambda }_1}{\displaystyle \underset{i=1}{\overset{t_1}{\sum }}\left({\alpha }_{1i}^{*}-{\alpha }_{1i}\right)}\frac{1}{\left|B_i^s\right|}{\displaystyle \underset{j\in B_i^s}{\sum }{x}_j}$ (8)

$v_2=\frac{1}{{\lambda }_2}{\displaystyle \underset{m=1}{\overset{t_2}{\sum }}\left({\alpha }_{2m}^{*}-{\alpha }_{2m}\right)}\frac{1}{\left|B_m^t\right|}{\displaystyle \underset{n\in B_m^t}{\sum }{x}_n}$ (9)

具体算法求解过程如表1所示。

Table 1. LPI-TL Algorithm

表1. LPI-TL算法流程

3.3. 时间复杂度分析

对于提出的LPI-TL算法，假设求解标准SVM的时间复杂度为 ${\rm O}\left({\left[数据量\right]}^2\right)$，则在本文中解决公式6等同于求解一个数据量为M个原任务样本和N个目标任务样本的标准SVM问题，则最终的时间复杂度为 ${\rm O}\left({\left(M+N\right)}^2\right)$。

4. 实验与分析

为验证所提出算法的有效性，本文设计了数据实验来验证所述方法，并采用Inv-Cal [8]，Alter-SVM [9] 和p-NPSVM [12] 作为对比方法。

4.1. 实验数据

论本文采用SRAA¹和20 Newsgroups²数据集，这两个数据集是用于文本分类、文本挖掘和信息检索研究的国际标准数据集之一,并被广泛用于迁移学习实验。SRAA数据集包含来自四个讨论组的7327个UseNet文章，里面包含着模拟赛车，模拟航空，真实汽车，真实航空四个主题的数据。20 Newsgroups数据集收集了大约20,000左右的新闻组文档，每个顶级类别下都有20个子类别，每个子类别都有1000个样本。有一些新闻之间是相关的，比如Sci.elec vs. Sci.med；有一些新闻是不相关的，比如Sci.cryptvs.Alt.atheism。

由于上述两个数据集不是专门为LLP问题设置，需要将文本数据集重新组织为适用于标签比例学习问题的数据集。采用文献 [15] [16] 处理上述数据集的方法，我们根据数据集的顶级类别重新组织LLP数据集。首先，我们从顶级类别(A)中选择一个子类别a(1)作为正类别，因此将该子类别a(1)中的每个样本视为正类样本，其他顶级类别作为负类别。其次，对于原任务，我们从正子类别a(1)中随机选择多个样本作为正样本，并从其他类别中随机选取相同数目的样本作为负样本，并将它们组成为原任务数据集。对目标任务执行相同的操作以形成正类样本和负类样本。为了使两个任务相关，我们让原任务和目标任务的正类具有相同的顶级类别，例如原任务为a(1)，则目标任务为a(2)。在不损失有效性的情况下，我们仅保留具有较高文档频率的单词以减少维数，并且每个样本均由特征表示。最后随机选取同等比例的正样本和负样本生成5个数据集，如表2所示。

Table 2. The list of data sets

表2. 数据集列表

4.2. 实验设置

为减少包中样本数量对实验结果的影响，本实验从每个数据集中分别随机选择20，40和60个样本组成包，并分别对大小不同的包依次进行实验，其中对四个算法的参数设置如下：

Inv-Cal： $C\in \left[2^{-2},2^5\right],\epsilon \in \left[0.01,0.1\right]$。

Alter-SVM： $C\in \left[2^{-2},2^5\right],C_p\in \left[2^{-2},2^7\right]$。

p-NPSVM： $C_i\in \left[2^{-5},2^5\right]\left(i=1,2,3,4\right),C_p\in \left\{0.1,1,10\right\}$。

LPI-TL： $C_i\in \left[2^{-2},2^7\right]\left(i=1,2\right),\epsilon \in \left[0,1\right]$。

其中本文方法使用线性核函数 $K\left(x_{\text{1}},x_{\text{2}}\right)=x_{\text{1}}\ast x_{\text{2}}$，采用五折交叉验证法进行实验。由于Inv-Cal，Alter-SVM和p-NPSVM为单一任务算法，对其只在目标数据集上进行实验，对提出的算法则使用原任务数据集和目标任务数据集进行实验。

4.3. 实验结果分析

首先，利用本文提出的基于标签比例信息的迁移学习算法迁移原任务数据知识来对目标任务数据集进行实验，并采用准确率、精度、召回率和F1值等评价指标与Inv-Cal，Alter-SVM和p-NPSVM对比。

五个数据集具体的平均测试准确率和标准差实验结果如表3所示。表3表明，在数据集3包的大小为20以及数据集4包的大小为40和60中，本文提出算法比其他方法略低外，在其他实验结果中均能取得最高准确率和较低的标准差。图3展示了这四个算法的平均准确率的柱状图，其中四个算法的平均准确率分别为：62.44%、63.09%、63.38%和67.77%，可见提出的算法LPI-TL的平均准确率高于Inv-Cal，Alter-SVM和p-NPSVM三个算法。这表明提出的方法在通过迁移原任务数据知识在分类准确率上能取得较高且稳定的性能。

另外，为了将其他算法与提出的LPI-TL方法进一步比较，将对上面实验得到的准确率做Wilcoxon符号秩和检验 [17] [18]。通常，如果测试值p值低于置信度0.05，则LPI-TL与所比较的方法之间存在显著差异。对于每种方法，其与LPI-TL之间的测试结果列在表4中。从表中可以看出，每种方法对LPI-TL的p值均小于置信度0.05，这意味着在统计视角中，本文提出的算法LPI-TL比其他三个方法在准确率上取得显著性提高。

为了进一步验证本文提出算法的性能，对5个数据集在包为20的情况下分别计算准确率、召回率和F1值等指标的平均值。实验结果如表5所示。从表中可以看出，LPI-TL算法平均召回率比Alter-SVM算

Table 3. Experimental accuracy and standard deviation Statistics

表3. 实验准确率和标准差结果统计

Figure 3. The mean accuracy

图3. 平均准确率

Table 4. Wilcoxon signed ranks test.

表4. Wilcoxon符号秩和检验

Table 5. Performance comparison of each algorithm

表5. 各个算法性能对比

法低，这是由于Alter-SVM算法找出更多的负样本，所以召回率更高；相比之下，LPI-TL算法取得更大的精度和F1值。总体来看，本文提出的LPI-TL算法的结果比对比方法更佳。

5. 结束语

本文对基于标签比例信息的迁移学习进行了研究，为了目标任务能更有效的学习预测模型，本文提出了一种迁移学习的模型用于从标签比例信息中学习分类器，该方法能将知识从原任务迁移到目标任务，并可以帮助目标任务构建分类器。本文实施了大量的实验去研究该方法的性能，实验表明该方法优于现有的LLP方法。该方法的不足之处在于仅能处理二分类问题还无法处理多分类数据，将来希望将该方法应用于多分类问题，这个问题值得后续进一步研究。

基金项目

国家自然科学基金资助项目(61876044)。

NOTES

¹http://www.iesl.cs.umass.edu/datasets.html。

²http://qwone.com/~jason/20Newsgroups/。