1. 引言
在使用激光扫描仪采集点云数据的过程中,由于模型残缺、视线死角等原因,会导致局部数据缺失,使生成的三维模型表面不完整,存在孔洞。点云的空洞修补是根据孔洞附近点的数据信息,通过填充算法生成新点对孔洞进行填充,恢复物体模型的原始表面形状。点云孔洞修补技术已经被广泛应用于制造业、文物保护以及地形测量等领域 [1]。
现有的孔洞修补算法主要有Centin M和李月雯等人 [2] [3] 提出的泊松法、Liu和Gai等人 [4] [5] 提出的径向基函数法、刘震和Wang等人 [6] [7] 提出的特征线修补法、Wang 和刘许等人 [8] [9] 提出的移动最小二乘法等。
本文提出一种结合有序边表法和径向基函数的点云孔洞修补方法。用有序边表法对孔洞进行初步填充,用径向基函数分层调整填充点的位置,减少了填充时间,使点的分布更加均匀,提高了填充后网格的质量。
2. 孔洞的识别及填充
2.1. 孔洞边界的提取
在对三维点云进行填充之前要先获取点云孔洞的边界。在三角形网格内部中,每条边都参与组成两个三角形,而位于边界处的边只参与组成一个三角形,所以应先遍历已生成的所有边和三角形,将只属于一个三角形的边界边提取出来,将边界边首尾相接形成闭环,就得到孔洞的边界,如图1所示。
求得边界点集后,需要利用点集拟合一个二维平面,将空间点集投影到该平面上。本文采用最小二乘法来进行平面拟合。设其平面方程为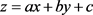 ,利用最小二乘法可以求解出平面参数。
,利用最小二乘法可以求解出平面参数。
2.2. 有序边表法填充孔洞
将孔洞边界投影到二维平面后,需要按照一定的密度向边界多边形内添加填充点,本文采用有序边表法实现孔洞的快速填充,如图2所示。具体步骤如下:
Step1:将多边形的所有边按照其上端点的y坐标递增的顺序进行排序,并放入边界边链表中,同时建立一个空的活性边链表。
Step2:建立一条与多边形最低点相交的水平线,称之为扫描线,其纵坐标大小标记为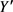 。
。
Step3:将扫描线沿y轴上升一段距离d (计算方法见2.2),将活性边链表中上端点y坐标小于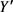 的边删除,同时将边界边链表中下端点y坐标小于
的边删除,同时将边界边链表中下端点y坐标小于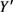 且上端点y坐标大于
且上端点y坐标大于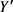 的边提取出来加入到活性边链表中。
的边提取出来加入到活性边链表中。
Step4:计算扫描线与活性边链表各边的交点,在扫描线上从左侧开始按照距离d取点作为填充点,且填充点与右侧交点距离应大于等于d/2。
Step5:重复执行Step3、Step4,直至活性边链表为空。

Figure 2. Ordered edge table fill polygon
图2. 有序边表法填充多边形
2.3. Delaunay三角剖分生成网格
孔洞填充完成后,需要用Delaunay三角剖分算法生成三角形网格,如图3所示,具体步骤为:
Step1:建立一个三角形,将所有的点包围在其中,称之为超级三角形;同时把散点按横坐标的大小进行排序。
Step2:从点集取出一个散点,在三角形链表中找出外接圆包含该点的三角形,称为该点的影响三角形。 删除影响三角形的公共边,将插入点同影响三角形的全部顶点连接起来,完成一个点在Delaunay三角形链表中的插入。
Step3:循环执行上一步,直到所有散点插入完毕;删除与超级三角形顶点有关的所有三角形。
 (a) 散乱点云
(a) 散乱点云  (b) 网格模型
(b) 网格模型
Figure 3. Generate mesh models from point clouds
图3. 由点云生成网格模型
3. 径向基函数调整填充点的位置
3.1. 径向基函数
对于三维空间的n个点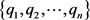 及对应的值
及对应的值 ,如果存在一个函数
,如果存在一个函数 满足
满足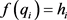 ,那么可以由
,那么可以由 定义一个隐式曲面。基于径向基函数的的隐式曲面方程通常表示为:
定义一个隐式曲面。基于径向基函数的的隐式曲面方程通常表示为:
 (1)
(1)
曲面方程中的参数可以通过求解如下矩阵方程来求得:
 (2)
(2)
其中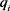 为约束点,
为约束点,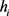 为约束点对应的值,当点在曲面上时
为约束点对应的值,当点在曲面上时 ,当点在曲面外侧时
,当点在曲面外侧时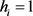 ,
,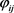 由下式求得:
由下式求得:
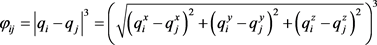 (3)
(3)
3.2. 确定点的法向量及提取约束点
使用径向基函数建立隐式曲面方程要先获取到足量的能表达物体几何特性的插值点信息,本文将边界点及其相邻的点添加为插值约束点,但若只在曲面上取点,会导致矩阵方程只有零解,生成的隐式曲面方程无法准确反映曲面在空间的曲率变化,因此还需要在曲面外取一些约束点。
在曲面外取点之前要先确定点的指向曲面外侧的法向量。先将空间划分成许多个小栅格并为其编号,确定每个散点所在的栅格。将边界点按照首尾相接的顺序排序,并均匀的取出六个点,对每一个点用最小二乘法求解出该点的近似法向量,然后分别沿XYZ坐标轴搜索,如果X轴正方向上的栅格都不包含其他点,而X轴负方向上的栅格内有其他点存在,则称该点的法向量可由X轴方向确定,且点的法向量应该与向量 的夹角为锐角,如果一个点可以由两个坐标轴方向来确定且结果一致的话,则可以取该点为基准点,根据相邻点方向量成锐角的原则,可以确定其他点的法向量。
的夹角为锐角,如果一个点可以由两个坐标轴方向来确定且结果一致的话,则可以取该点为基准点,根据相邻点方向量成锐角的原则,可以确定其他点的法向量。
然后在每一个曲面上约束点沿指向曲面外的法向量0.2单位长度处取点作为曲面外的约束点,将约束点坐标及取值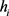 代入到矩阵方程中可以求解出隐式曲面方程的参数。
代入到矩阵方程中可以求解出隐式曲面方程的参数。
先计算出边界边平均距离 ,根据边界点的坐标求出其重心点C,采用2.3中的公式(4)进行迭代调整求出该点在隐式曲面上对应的点C',计算出两点间的距离
,根据边界点的坐标求出其重心点C,采用2.3中的公式(4)进行迭代调整求出该点在隐式曲面上对应的点C',计算出两点间的距离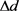 。则填充点的采样距离d可由
。则填充点的采样距离d可由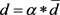 确
确
定,其中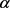 为比例因子,当
为比例因子,当 时,
时,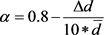 ,当
,当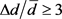 ,
,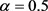 。
。
3.3. 调整填充点的位置
用有序边表法对投影后的孔洞进行填充后,需要通过逆矩阵变换将其映射回三维空间,映射后的点处在边界点的拟合平面上。需要将拟合平面中的新增填充点向隐式曲面逐步迭代调整,使新增的孔洞点与先前孔洞周围点云能够平滑过渡,更好的还原模型的几何特征,如图4所示。调整步骤如下:
Step1:遍历所有的新三角形,按照填充点之间的连接关系,确定填充点所在的层数,与边界点相连的点处于第一层。还需确定填充点与上一层哪些点相连,计算这些点的平均点作为填充点的基点。取边界边平均距离的1.5倍为临界距离。
Step2:从第一层开始,按照层数依次取出点进行调整,将该点的坐标带入函数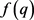 中,确定
中,确定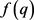 的正负号,然后用下式进行迭代
的正负号,然后用下式进行迭代
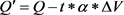 (4)
(4)
其中 分别为初始点坐标和调整后点的坐标;t为点的位置参数,当
分别为初始点坐标和调整后点的坐标;t为点的位置参数,当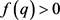 时
时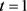 ,当
,当 时
时 ;
;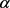 为步长,大小为边界边平均距离的十分之一;
为步长,大小为边界边平均距离的十分之一;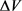 为拟合平面的单位法向量。
为拟合平面的单位法向量。
每迭代一次计算一下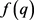 ,直到
,直到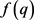 的正负号与初始
的正负号与初始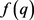 的正负号相反时,停止迭代。
的正负号相反时,停止迭代。
Step3:计算点与基点的距离,若大于临界距离,则取该点与基点线段上距基点距离等于临界距离的点替代该点。
Step4:循环执行Step2、Step3,直到所有点被调整完毕。
Step5:最后用拉普拉斯算法进行平滑处理,即将网格中的每个顶点移向其周围邻域重心的位置。
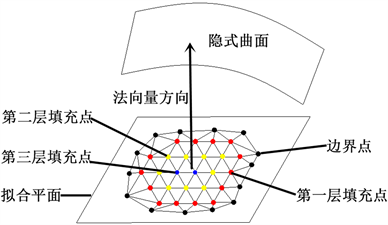
Figure 4. Layered adjustment of fill points
图4. 填充点的分层调整
4. 实验结果及分析
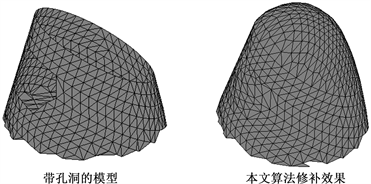
为了验证提出算法的有效性,在Win7环境下用C++编写程序,使用OpenGL图形库对点云和网格进行渲染,使用 MFC 框架实现可视化界面。实验计算机配置为Intel(R) Core(TM) i5-4590 3.30 GHz CPU,8 G运行内存,修补实例如图5所示。
 (a) Circular cone
(a) Circular cone 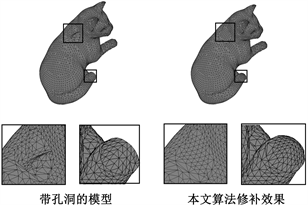 (b) Cat
(b) Cat 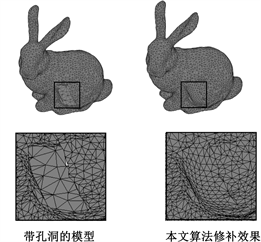 (c) Rabbit
(c) Rabbit
Figure 5. Hole repair example
图5. 孔洞修补实例
5. 结论
本文提出了一种高效率的点云孔洞修补算法,用有序边表法生成填充点对孔洞进形填充,避免了复杂的角度运算,缩短了填充时间。然后用栅格法确定约束点法向量的方向,准确地求出径向基函数的隐式曲面方程,根据曲面方程对添加的填充点逐层进行调整,最后对所有点用拉普拉斯算法进行平滑处理,使填充点的分布更加均匀。实验结果表明,该算法对于孔洞具有很好的填充效果,对点云模型的适应性比较好,对于曲率变化显著的孔洞也能够准确地进行修补,生成的曲面与原有孔洞边界过渡平滑,可以较精确地恢复模型的表面形状。