置于不同基底表面的单一金纳米粒子的近场特性

Near-Field Properties of a Single Gold Nanoparticle Placed on Various Substrate Surfaces

摘要: 本文采用时域有限差分方法仿真研究了金粒子在金属(金)，半导体(硅)和电介质(二氧化硅)基底表面经飞秒激光激发后的近场(电场)特性。仿真结果表明，在三种基底条件下，基底表面的电场均被增强，但电场的强度、空间分布以及尺寸大小均取决于基底材料。在金属基底和半导体基底条件下，电场被局限在粒子与基底的接触点周围。由于基底材料的不同，导致能够产生最大增强因子的共振波长发生偏移。该研究对于调控增强因子，实现超衍射极限纳米结构的精细加工具有重要意义。

Abstract: In this paper, the finite-difference time-domain method is used to simulate the near-field (electric field) characteristics of a single gold nanoparticle on the surface of a metal (gold), semiconductor (silicon), and dielectric (silicon dioxide) substrate excited by a femtosecond laser. The simulation results show that the electric field on the substrate surface is enhanced under three substrate conditions, but the strength, spatial distribution, and size of the electric field all depend on the substrate material. Under the conditions of metal substrates and semiconductor substrates, the electric field is confined around the contact points between the particles and the substrate. Due to the difference of the base material, the resonance wavelength that can produce the maximum enhancement factor is shifted. This study is of great significance for regulating enhancement factors and achieving fine processing of ultra-diffraction-limited nanostructures.

1. 引言

飞秒激光由于其超快超强的特性，在加工中具有精度高、无污染、控制灵活等优势，因此被广泛应用于国防、生物、医疗等领域。但随着器件的微小型化成为发展趋势，由于光学衍射极限的制约，低于衍射极限尺度的激光加工成为技术难题。近年来研究发现，飞秒激光辐照基底表面的纳米粒子时，能够在粒子和基底的接触点附近获得一个远小于光学衍射极限分辨率的增强的近场，并且可以利用近场在低于基底本身的烧蚀阈值的条件下，在接触点实现纳米尺度的表面加工 [1] [2] [3]。这为飞秒激光纳米加工指出了一个新的方向。

Takada H.等人 [4] 采用时域有限差分方法(FDTD)分别仿真模拟了波长800 nm的飞秒激光激发直径200 nm、450 nm和820 nm的聚苯乙烯(PS)纳米粒子在有机玻璃(PMMA)基底上的近场增强效应。结果表明基底内部的电场强度随着纳米粒子直径的增加而增大；S. M. Huang等人 [5] [6] 同时运用仿真模拟和实验两种方法研究了低折射率介电纳米粒子(二氧化硅纳米粒子)在金属基底表面的近场增强效应。实验使用单发飞秒激光脉冲辐照金属表面的二氧化硅纳米粒子，并通过扫描电子显微镜和原子力显微镜对金属基底表面的烧蚀形貌进行表征。在相同的脉冲通量条件下，烧蚀孔的直径和深度随着纳米粒子直径的增加而增大；当纳米粒子直径不变时，随着入射激光通量的升高，烧蚀孔的直径和深度也随之增大。实验结果与仿真模拟相吻合，并得出结论：对于非吸收性纳米粒子，入射光可以激发粒子内部的一些共振模式，并在接触区域产生增强的电场。Afanasiev和Bityurin [7] [8] 等人仿真研究了不同波长的飞秒激光(400 nm和800 nm)激发PMMA基底表面直径为450 nm的聚苯乙烯纳米粒子阵列的近场增强效果，发现粒子对400 nm波长激光的汇聚效果要远优于800 nm波长的激光。目前大部分的纳米粒子辅助飞秒激光加工的研究均采用时域有限差分方法进行仿真研究，该方法是电磁场数值计算的重要方法之一，通过该方法可以直接获得基底表面电场的空间分布以及强度数值，通过电场强度及其分布就可以预测现实加工中获得的烧蚀形貌，对实验具有指导意义。

随着对纳米粒子近场增强效应的研究，金纳米粒子由于优秀的近场增强特性和只需要简单的设置就可以实现快速的大面积加工的优势，而受到广泛的关注 [9] [10]。但对于基底材料和入射激光波长对金纳米粒子近场增强能力的影响还未有较全面的研究。因此，本文采用FDTD数值仿真方法，研究了不同波长的飞秒激光激发直径为200 nm的孤立金纳米粒子在金基底，硅基底以及二氧化硅基底表面的近场特性(电场分布和增强因子)，为日后的实验研究起到指导作用。仿真结果表明基底的改变使得激发金粒子最佳近场增强因子的共振波长发生了偏移，因此对于不同基底选择不同的入射激光波长来控制近场增强效果是一种有效的途径。

2. 仿真模型

本文采用FDTD Solutions软件对飞秒激光激发的金纳米粒子的近场增强效应进行了仿真研究，仿真模型如图1所示。直径为200 nm的金纳米粒子孤立置于基底表面，纳米粒子周围为真空环境。仿真区域以粒子心为中心，尺寸为300 × 300 × 400 nm³，网格精度为1 × 1 × 1 nm³。所用入射光源为全场散射场(total field scattered-field, TFSF)光源，沿z轴负方向垂直入射于纳米粒子和基底表面，偏振方向与x轴平行。周围为完全吸收边界，监视器位于y = 0的xz平面和z = 0的xy平面。在仿真过程中设置的模拟时间是1000fs(保证有足够时间使结果收敛)，设置使得仿真在满足auto shut off level (默认设置是10-6)后自动结束，这样保证了仿真精度和结果的可靠性。

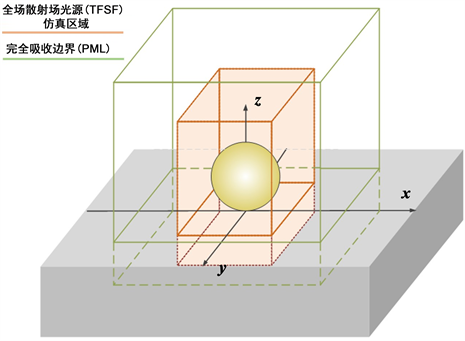
Figure 1. Schematic diagram of FDTD simulation. A single gold particle with a diameter of 200 nm is placed on the surface of the substrate. Total field scattered-field light source incident in reverse along the z-axis, the polarization direction is parallel to the x-axis, and the incident electric field intensity is 1 V/m. The surrounding is a complete absorption boundary

图1. FDTD仿真模拟示意图。直径为200 nm的金粒子孤立置于基底表面。全场散射场光源沿z轴反向入射，偏振方向与x轴平行，入射电场强度为1 V/m。周围为完全吸收边界

3. 结果与讨论

在仿真模拟中经常采用增强因子 $Q=\left|E^2\right|/\left|E_0^2\right|$ 来评估近场的增强效果，其中E²为有粒子时基底表面的光强， $E_0^2$ 为入射光强，Q值越大表示粒子在基底表面增强近场的能力越强。当入射激光波长为800 nm时，置于金、硅和二氧化硅基底表面的金粒子周围的电场强度分布如图2所示。粒子表面的电荷振荡引起了粒子附近的一个增强场，由于基底表面镜像电荷的感应和近场的倏逝特性，场增强的区域被局限于粒子与基底的接触点附近 [11]。结果表明，在金基底条件下获得的近场强度最大，硅基底次之，二氧化硅基底则是最小的。在金属(Au)和半导体(Si)基底的条件下，最大的场增强区域紧紧聚集在粒子和基底的接触点附近，而在二氧化硅基底上则没有明显的表现出局域的特性。

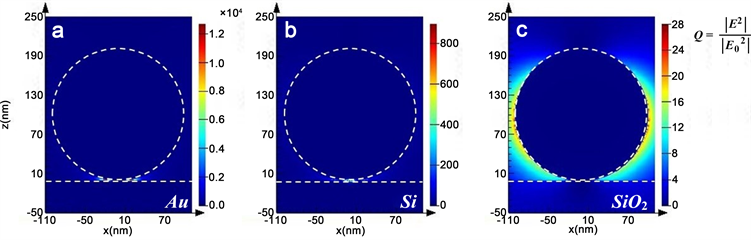
Figure 2. Electric field distribution of a single gold particle placed on the surface of different substrates (a) Gold, (b) Silicon, (c) Silica in the x-z plane. The plane passes through the contact point between the particle and the substrate

图2. 置于不同基底(a) 金、(b) 硅、(c) 二氧化硅表面的单一的金粒子在x-z平面的电场分布，平面穿过粒子与基底的接触点

基底表面的电场分布如图3所示。在激光偏振方向，粒子和金基底表面的接触点两侧出现两个极强的近场区域，如图3(a)所示；在硅基底表面以接触点为中心形成了向外扩散的波纹结构的电场分布，电场强度随着波纹结构的扩散而逐渐减弱，并且在硅基底表面的电场相比于在金基底表面更加集中，特征尺寸更小如图3(b)所示；在二氧化硅基底的表面形成了了两个尺寸较大，近似扇形的场增强区域，强度远也小于金基底和硅基底表面获得的电场强度，如图3(c)所示。

Figure 3. Electric field distribution of gold particle on the surface of different substrates (a) gold, (b) silicon, (c) silicon (x-y plane with z = 0)

图3. 标准试验系统结果曲线

对于近场增强因子的大小，近电磁场与基底的耦合是主要影响因素。当粒子置于非金属材料表面时，金粒子表面的强场将会在基底表面诱导产生镜像电荷 [12] [13]，由于衬底表面的镜像电荷及其反射系数是衬底介电性能的函数，因此不同的衬底材料具有不同的场特性。由于各自的镜像电荷效应，在不同的衬底上电耦合的大小表现不同。衬底中的镜像电荷表示为：

$q^{\prime }=\frac{{\epsilon }_s-{\epsilon }_a}{{\epsilon }_s+{\epsilon }_a}q$ (1)

其中 $q^{\prime }$ 为镜像电荷，q为诱导镜像电荷的初始电荷， ${\epsilon }_s$ 为基底的介电常数， ${\epsilon }_a$ 为空气的介电常数。由公式(1)可知，随着衬底介电常数的增加，衬底上的镜像电荷增加，因此硅基底相比于二氧化硅基底产生了更强的电磁耦合，导致了更大的增强因子。而金属材料本身含有大量的自由电子，其电偶极共振模式产生的近场增强则远高于非金属材料。

为了研究入射激光波长对近场增强因子的影响，在波长范围300~1000 nm内改变入射激光波长对结构进行仿真模拟，并对基底表面的近场增强因子进行统计，绘制出增强因子随入射激光波长的变化曲线，如图4所示。当粒子在金基底表面时，在波长小于500 nm的条件下，基底表面的增强因子较低且几乎保持不变，随着入射激光波长的增加，增强因子先呈指数升高，在入射波长700 nm时达到最大值88354.6，随后又迅速降低。金粒子在硅基底表面的增强因子在入射波长大于400 nm后增强因子开始出现较明显的升高，并且在入射波长600 nm和750 nm处出现了两个峰值，产生最大增强因子的共振波长相比于在金基底表面发生了偏移，在波长600 nm处达到增强因子的最大值2976.4，这一数值远低于在金基底表面所产生的增强因子最大值。金粒子在二氧化硅基底表面产生的最大增强因子的共振波长相对于前两种基底材料继续偏移，在波长550 nm时增强因子达到最大值且仅为24.8966，远低于前两种基底材料。

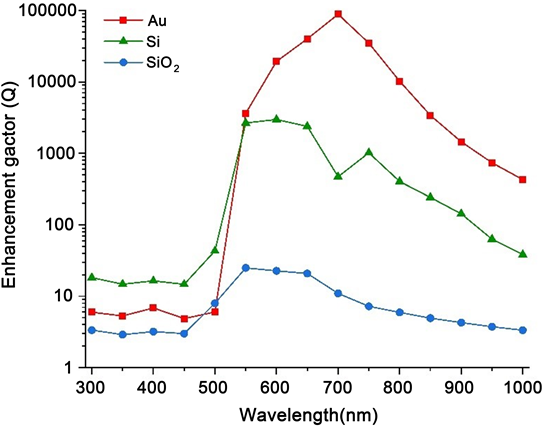
Figure 4. Curve of substrate surface enhancement factor as a function of incident laser wavelength

图4. 基底表面增强因子随入射激光波长的变化曲线

由于近电场是由电荷振荡所激发的，因此对于粒子在不同基底表面的共振波长发生偏移的情况，可以用粒子的近场散射效率来解释 [14] [15]。近场散射效率与粒子将入射电磁场强度转化为近场强度的能力有关，与场增强因子成正比，散射效率的公式描述如下 [16] [17] ：

$Q_{nf}=2{\displaystyle {\sum }_{n=1}^{\infty }\left\{{\left|a_n\right|}^2\left[\left(n+1\right){\left|h_{n-1}^{\left(2\right)}\left(k_{0}R\right)\right|}^2+n{\left|h_{n+1}^{\left(2\right)}\left(k_{0}R\right)\right|}^2+\left(2n+1\right){\left|h_n^{\left(2\right)}\left(k_{0}R\right)\right|}^2\right]\right\}}$ (2)

其中 $a_n$ 和 $b_n$ 为米散射系数；n为振荡模式数；介质波数 $k_0=2\text{π}{n}^{\prime }/\lambda$， 和 $\lambda$ 分别为周围介质的折射率和入射激光波长；R为纳米粒子的半径， $h^{\left(2\right)}\left(x\right)$ 为第二类球形汉克尔函数。从上式可以看出，基底的折射率和入射激光波长同时影响到粒子的近场散射效率，基底和入射激光波长特定的组合才能够实现当前基底条件下最大的近场增强效应。

4. 结论

本文主要研究了直径200 nm的金纳米粒子在三种不同的基底表面的近场特性，仿真结果表明三种基底表面的电场均有增强，但电场的强度、空间分布和尺寸均取决于基底材料。由于基底材料的不同，使得产生最佳增强因子的共振波长发生偏移，因此能够通过改变入射激光的波长对基底表面的增强因子进行调控从而实现基底表面加工形貌的调控。

NOTES

^*通讯作者。