1. 引言
铁路作为我国主要的经济命脉,为我国的发展注入了长足的动力。我国也一直为提高铁路的运输能力,增强铁路在市场中的竞争力而不懈努力。在国家“交通强国”目标的指引下,重载铁路运输以其对环境造成的污染小、运输能力强、效率高、低碳环保的优势,迅速成为承担大宗货物运输的主要力量 [1]。但在重载列车的运行过程中,往往会产生比较大的纵向冲动,导致列车断钩、脱钩的事故常有发生,因此深入研究重载列车纵向动力学是十分必要的。在重载列车的实际运行过程中,由于开行密度大,列车的编组较长,依靠试验来解决所需的费用是十分昂贵的,并且试验条件也是极其有限,不能大规模推广。所以列车纵向动力学仿真分析的研究便提上日程,该方法以其独特的经济性以及便于操作性大大弥补了现场试验的不足,从而得到广泛应用。
Belforte使用Matlab软件对欧洲重载铁路纵向动力学进行了仿真研究,探究了列车编组方式对列车运行安全的影响 [2];Colin Cole通过对澳大利亚昆士兰铁路和南非Spoornet的比较,对动力分散列车的优点进行研究 [3] [4];靳新元根据两万吨重载组合列车的试验数据,分析了列车在长大下坡道车钩的受力情况 [5];白建凌对两万吨重载列车在长大坡道上运行时制动力的判断标准以及调整方法进行了探究,提出了“三定一调”的操纵方法 [6];杨敏根据HXD2型电力机车双机重联牵引万吨重载列车,建立了列车纵向动力学模型 [7];董克毓针对万吨列车在神朔长大下坡道的实际操作情况进行了分析 [8];张帅根据列车牵引计算理论,建立机车牵引与电制动力学模型并验证了其有效性 [9];耿志修建立了重载列车运行仿真计算模型,研究了在不同编组下重载列车的牵引、制动参数,为大秦线的操纵方法做了指导 [10];魏伟、赵连刚通过仿真获得1 + 2 + 1编组两万吨列车制动特性,并且计算了列车车钩力的分布特性 [11]。宋健针对重载列车纵向冲动问题,对制动系统传动效率与机车电制动系统模型进行修正,提高了仿真系统精度 [12];杨兴光对重载列车在惰行、电制动和电空混合制动三种工况下进行研究,将仿真结果与实验结果进行比较,证明了仿真系统准确性高 [13];袁梓铭针对重载铁路运行阻力进行研究,通过仿真程序提出新的基本运行阻力公式,提高了计算精度 [14]。
虽然众多学者对重载列车在下长大坡道的操纵优化问题做了较多研究,但针对缓解之后电制动力的调节并未做深入研究,而且目前两万吨重载列车在长大坡道运行时仍然会产生比较大的纵向冲动,针对此的优化方案并未完善。在2017年,关于列车纵向动力学仿真系统牵引与制动的工况,在6个国家,9套仿真系统的评测中,TABLDSS凭借计算精度以及计算速度取得了优异成绩 [15]。本文通过该仿真程序TABLDSS针对两万吨列车在长大下坡道的仿真,探究了主、从机车电制动力的异步控制对缓解时产生的最大车钩力的影响,提出了一种新的优化方案。
2. 列车纵向动力学仿真模型
在研究列车纵向动力学时,机车、车辆的横向以及垂向动力学运动被忽略,将列车抽象为一个多质点的质量弹簧阻尼系统,每个机车车辆看成只有一个自由度的质点,各个质点之间通过弹簧阻尼器相连接,整列车的自由度为机车车辆总数n,现取单一车辆为研究对象分析其受力情况如图1所示。

Figure 1. The force diagram of single vehicle
图1. 单个车辆受力图
每个车辆力平衡方程式为:
(1)
(2)
式中:
n:列车中包含的机车车辆总数;
:第i节车的惯性力;FGi:第i对车钩的车钩力;
FAi:第i节车运行阻力;FBi:第i节车所受的空气制动力;FLi:牵引力或动力制动力;
FWi:第i节车所受的坡道阻力;FCi:第i节车所受的曲线阻力。
方程(1)共有n个方程,通过求解该方程组就可以获得每个车辆的加速度。再利用加速度与速度、位移间的关系,就可以获得列车中每一个车辆在纵向冲动中的各种运动参数。
3. 线路条件
本文的研究对象为某重载铁路上运行的两万吨重载组合列车,采用的编组形式为1HXD1 + 108C80 + 1HXD1 + 108C80 + 可控列尾。该重载铁路运营里程达到近600 km,相对海拔高度的落差可以达到1527 m。连续的长大下坡道众多,线路的纵断面坡度最高可以达到12‰,其中最为典型的一段路长12800 m,下坡道坡度达到10.2‰。同时,在这段区间内,线路还有曲线,最小的半径只有400 m,再加上桥涵、隧道众多,列车的编组长等客观原因,使得列车的纵向冲动大,容易产生比较大的拉钩力以及压钩力,操纵起来十分困难(图2)。操作不当容易使列车被迫停车,甚至发生脱轨事故,成为影响列车行车安全的主要影响因素。所以通过仿真深入探究列车在运行过程的纵向冲动问题,制定合理的优化操纵方案,对现实具有重大的指导意义。
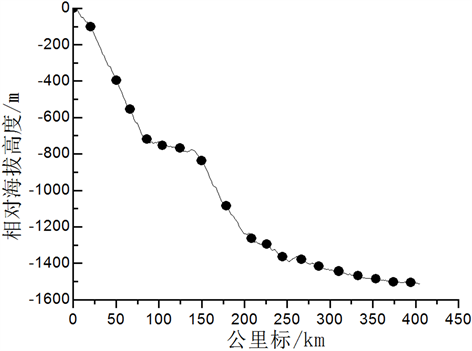
Figure 2. Line relative altitude curve
图2. 线路相对海拔高度曲线图
4. 主从控机车异步控制及优化结果
4.1. 主、从控机车异步控制对最大车钩力的影响
目前重载列车在运行过程中,传统的主、从控机车对电制动力是同步进行控制,电制动力的不同会影响列车所受到的最大车钩力的情况。但在同步控制的情况下,由于列车的编组是“1 + 1 + 0”的形式,列车在缓解时,主、从控机车分别向列车前后车辆进行充风,各车位从列车管开始充气到制动缸开始排气存在一定的时间差,不同步性使列车前后部缓解开始时刻存在时间差,往往导致前部车辆先缓解有增速趋势,对后部还未缓解的车辆产生拉伸作用,从而出现比较大的拉钩力;出现最大拉钩力之后,由于列车的伸缩震荡以及前部车辆的堵截,导致后部车辆挤压前部车辆,从而出现最大压钩力 [16]。某重载铁路长大下坡操纵困难路段,里程为24.2~29.9 km,该段的特殊之处在于无变坡点,坡道千分数为10.2‰,按照常规的操纵方法,列车在25.9 km处制动,在28.6 km处缓解,此时的缓解速度为40 km/h,缓解之后主控以及从控机车的电制动保持310 kN不变,车钩力在列车缓解时随时间变化的曲线以及列车最大车钩力的分布情况如图3、图4所示。可以发现,列车在缓解时所受到的最大拉钩力为1257.2 kN,出现在109车位,最大压钩力为−864.6 kN,出现在140车位。
如果可以调整主、从控机车的电制动力,实现主、从控机车的异步控制,通过增加主控机车电制动力抑制前部车辆的增速趋势,并且通过降低从控机车电制动力使后部车辆的速度增大,进而使后部车辆向前涌,后部车辆挤压前部车辆,形成压缩车钩的趋势,对本已经拉伸的车钩起到一定的减缓作用,从而降低列车所受到的最大拉钩力;在出现最大拉钩力之后,为了防止坡道下滑力和机车电制动力的共同作用下产生的较大压钩力,减小主、从控机车的电制动力,由于在最大拉钩力出现之前先将主控机车电

Figure 3. The time-field curve of coupler force
图3. 列车车钩力时域曲线图
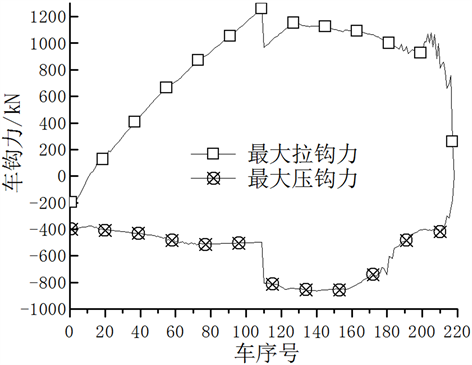
Figure 4. The distribution of the maximum coupler force
图4. 列车最大车钩力分布情况
制动力增大,前部机车大的电制动力使得列车钩缓装置并未充分拉伸,其反弹力是比较小的,出现最大拉钩力时再叠加上比较小的电制动力,使得后部车辆对前部车辆的挤压作用减小,从而降低列车的最大压钩力。为进一步验证上述推论,根据HXD1型电力机车允许的最大电制动力为461 kN [17],在里程为24.2~29.9 km的长大下坡道上,在允许的最大范围内在列车缓解时将主控机车的电制动力分别增大到380 kN、400 kN和450 kN,从控机车电制动力逐渐降低到100 kN、150 kN、200 kN,分别进行组合,实现主、从控机车对电制动力的异步控制,现选取如下九种方案进行探究,并对列车出现的最大车钩力进行统计,具体如表1所示。
由方案一、二、三对比可知,在列车缓解时从控机车电制动力降低到一定值,主控机车电制动力逐渐增大的情况下,列车所受到的最大拉钩力是逐渐减小的,主要是因为主控机车电制动力越大,对前部列车的抑制作用越明显,后部车辆在从控机车电制动力减小后增速,形成压缩车钩的趋势从而降低列车所受到的最大拉钩力;由方案一、四、七对比可知,在列车缓解时主控机车电制动力增加到一定值,当从控机车电制动力分别降低到不同值时,主控机车电制动力与从控机车电制动力之间的差值越大,列车所受到的最大拉钩力是越小的,主要是因为从控机车电制动力减小的越大,后部车辆的增速趋势越大,越容易形成往前涌的的趋势,从而降低列车的最大拉钩力;对比方案一到九可知,在出现最大拉钩力时将主、从控机车的电制动力降低是可以减小列车所受到的最大压钩力的,并且随着主、从控机车电制动力降低的越小,列车所受到的最大压钩力越小,主要是因为出现最大拉钩力之前主控机车有比较大电制动力,使得列车车钩在后期的反弹力变小,出现最大拉钩力时再叠加上比较小的电制动力,前部车辆对于后部车辆的堵截变小,后部车辆对前部车辆形成的冲击变小,从而减小列车所受到的最大压钩力。

Table 1. The plan of asynchronous control of main and driven control locomotive
表1. 主、从控机车异步控制方案
4.2. 主、从控机车电制动降低时刻对最大压钩力的影响
由3.1分析可知在列车缓解后出现最大拉钩力时,将主、从控机车的电制动力降低可以减小列车所受到的最大压钩力,但从出现最大拉钩力至出现最大压钩力这段期间内,主、从控机车的电制动力降低时刻是否对最大压钩力有影响,现对这一问题进行探究。在里程为24.2~29.9 km路段上,最大拉钩力出现时刻是缓解后23 s,最大压钩力出现时刻是缓解后40.7 s。现将最大拉钩力出现的时刻记为0 s,从这一时刻往后依次延迟的时间记为∆t (s)。图5是从最大拉钩力出现时刻依次延迟一定时间后,将主、从控机车电制动力减小到100 kN时,对列车最大压钩力的影响。可以发现,随着延迟时间∆t的逐渐增大,列车最大压钩力是逐渐增大的,当∆t = 11 s、12 s、13 s时,列车所受到的最大压钩力依次为−786.9 kN、−994.7 kN、−1006.7 kN。这主要是因为列车在出现最大拉钩力后如果立即将主、从控机车的电制动力降低,列车在接下来的伸缩震荡过程中,前部列车对后部列车的堵截作用减小,从而避免后部列车挤压前部列车形成较大的压钩力;但如果在出现最大拉钩力后,当延迟时间∆t逐步增加到10 s以上时,由于并未及时将前部车辆的堵截作用减弱,列车在这期间由于伸缩震荡已经形成压钩趋势,再将主、从机车的电制动力降低时,形成的压钩力比之前的要大。所以要想降低列车在缓解时出现的最大压钩力,将主、从控机车电制动力降低要把握好时机,从最大拉钩力出现时刻开始,往后延迟的时间∆t应该控制在10 s以内为宜。
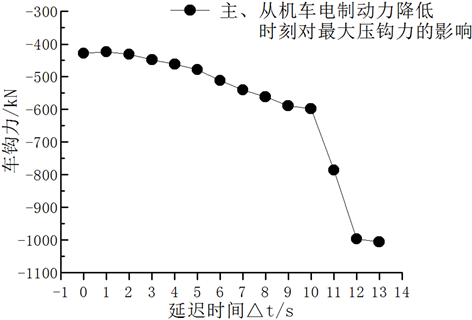
Figure 5. The influence of reducing time of electric braking force of main and driven controllocomotive
图5. 主、从控机车电制动力降低时刻的影响
4.3. 主、从机车异步控制优化方案探究
针对该重载铁路上的一段,里程为24.2~29.9 km,根据上述方案对其进行优化,具体结果如图6所示。可以发现优化前列车在缓解之后产生的最大拉钩力为1257.3 kN,优化之后最大拉钩力降为1153.8 kN,降低了8.2%;最大压钩力在优化之前为−864.6 kN,优化之后最大压钩力降为−412.6 kN,降低了52.3%。为了进一步验证该优化方案,选取该重载铁路的另一段,里程为192.3~199.0 km,列车在193.2 km处制动,在197.3 km处缓解,缓解速度为48 km/h,缓解时列车的电制动力为350 kN,具体结果如图7所示。优化之前,列车受到的最大拉钩力为778.5 kN,优化之后降为684.6 kN,降低了12.1%;最大压钩力为−800.6 kN,优化之后降为−401.1 kN,降低了49.9%。综合以上分析,该优化方案对于减小列车在缓解之后产生的比较大的车钩力是具有显著效果的。

Figure 6. The curve of the maximum coupler force before and after optimization
图6. 优化前后最大车钩力的变化曲线

Figure 7. The curve of the maximum coupler force before and after optimization
图7. 优化前后最大车钩力的变化曲线
5. 结论
通过以上探究,可以得出以下结论:
1) 重载列车在缓解之后往往会出现一个比较大的拉钩力与压钩力,通过主、从控机车电制动力的异步控制,可以减小最大车钩力。
2) 通过增加主控机车电制动力抑制前部车辆的增速趋势,降低从控机车电制动力使后部车辆的速度增大,使后部车辆向前涌,形成压缩车钩的趋势,减小列车所受到的最大拉钩力。
3) 通过在出现最大拉钩时降低主、从控机车的电制动力,可以减小列车在缓解之后受到的最大压钩力;但是出现最大拉钩力后随着延迟时间∆t的逐渐增大,再将主、从控机车的电制动力降低时,列车最大压钩力是逐渐增大;所以主、从控机车电制动力降低时刻应该在出现最大拉钩力后10 s内完成。