1. 引言
当前,自然语言处理研究日益成为人工智能研究的热点,研究的主要技术手段是基于统计学或基于深度神经网络机器学习这两种技术,并取得了许多非常有价值的研究成就。但是,这两种方法没有有效地利用语句中的语义信息,没有语义分析计算环节,影响了其分析处理的效果。
为了在自然语言处理中更加有效地利用语义分析,取得更好的研究效果,不少学者在原有技术的基础上,通过引入语义分析计算的方法来进行自然语言处理的研究。陈谦研究了基于循环神经网络的自然语言语义表征方法,利用了注意力机制来关注篇章的特定区域、内容,同时设计了分散力机制去遍历篇章的不同内容,从而更好地为摘要获取篇章的全局信息 [1];彭敏等研究了一个基于双向LSTM语义强化的概率主题模型来实现文档宏观语义的嵌入表示,采用文档–主题和词汇–词汇双语义强化机制以及LSTM来刻画参数推断过程中的吉布斯采样过程,可以提高文本语义特征表达方面的有效性 [2];贾玉祥等研究了采用神经网络技术的语义选择知识获取模型,设计了引入预训练词向量的单隐层前馈网络和两层maxout网络,在汉语和英语的伪消歧实验中神经网络模型取得了较好的效果 [3];Mikolov等通过词向量模型工具Word2vec来描述语义信息,具有较好的语言学特性,可在很多应用和任务改善自然语言处理效果 [4];Mikilov等人对词向量的研究非常具有开创性,引起了围绕词向量训练的热潮。Word2vec基于词频和上下文建立语言模型和训练词向量,有研究者考虑用更复杂的方式来训练,利用统计出的语言学规律,给词向量赋予更多的语义信息 [5];Pennington等提出GloVe模型,综合运用词的上下文统计信息,用共现矩阵来生成对数线性语言模型和词向量表示 [6];孟凡擎等通过依存句法分析,获取语料上下文知识,构建上下文词汇语义消歧图,进行依存句法分析,完成歧义词的消歧处理 [7];唐善成等研究了采用Seq2Seq模型的非受限词义消歧方法,输入词上下文序列,经过编码器编码得到潜在语义向量,再经过解码器解码输出词义序列 [8];夏小强等通过将PV-DM模型作为句向量训练基本模型,添加关系信息知识约束条件,能够学习到文本中词语之间的关系,进一步整合语义关系约束信息,能够更好地表示文本 [9]。
虽然这些研究已经获得了许多重要的学术成果,但迄今为止,并没有形成一个系统、有效的自然语言处理语义模型,其计算方法,依然有很大的改进余地。为了在自然语言处理更有效地使用语义信息,本文作者已经做了一些研究,可以通过语义计算,获取语句的语义修饰关系图 [10],在该文中,提出了简单语义单元的概念,但并没有得到很好地解决其语义修饰关系图的求解问题。为了解决这个问题,本文对简单语义单元的语义修饰关系图的求解方法进行了进一步的研究,设计近似算法,可以求出语义修饰关系图的最大生成树;实现了简单语义单元的语法、语义分析,并实现语义消歧。
2. 理论基础
2.1. 简单语义单元的定义
假设有一个短文本L,其词汇序列为L = Wm … W0,且Wi是L中的一个实词,词汇WGi是词汇Wi的语义修饰目标,函数match(Wi, WGi)来表示Wi和WGi之间的语义相关度,假如L满足如下的语义特征,则称L为一个简单语义单元:
i)
;
ii) L中不包含从句,也不包含谓语;
iii) L中不包含形式为WL1 … WL2…,或… WL3 …的虚词WL1、WL2、WL3;这些虚词具有连接、分段作用。
2.2. 简单语义单元所具有的语义特征
通过简单语义单元的定义进行分析,可以知道简单语义单元具有如下的语义特征:
i) 除了最后一个词汇W0,任何词汇Wi的语义修饰目标WGi,都在简单语义单元内部;
ii) 简单语义单元内部,没有复杂的内部语法结构需要处理;
iii) 进行语法、语义分析时,可以把简单语义单元作为一个整体来处理,其内部语法、语义结构对语句其余部分的分析结果没有影响。
2.3. 简单语义单元在自然语言处理中的作用
在自然语言处理过程中,可以把语句转化为多个简单语义单元,再进行处理,其方法如下:
2.3.1. 分割语句并获取简单语义单元
假设语句CS的语义、语义结构可以表示为:CS→LSLOLVL,并假定每个分段L是已经被分割成为“不包含从句”的程度,就可以根据分段L内各部分语义修饰目标的不同,将L划分为:前置定语、后置定语、状语(分别用AB、AA、PD表示)。就可以把L就转化为三个简单语义单元:AB + S、A A+ S、PD + V (见图1)。

Figure 1. The method of turning sentences into the simple semantic units
图1. 把语句转化为简单语义单元的方法
2.3.2. 含有分段、连接词的简单语义单元
经过2.3.1中方法的处理,假如某个简单语义单元中还包含有形式为WL1 … WL2 …,或… WL3 …的虚词。则可以用如下的方法将其转化为多个简单语义单元。
假设简单语义单元内包含了形式为WL1 … WL2 …的虚词;那么,简单语义单元内就被划分出两个语义块B1、B2;语义块B1的范围显而易见,B2的后界限Wi,可以通过式(1)来确定(见图2):
(1)
其中的W1~Wp与W的词性相同。
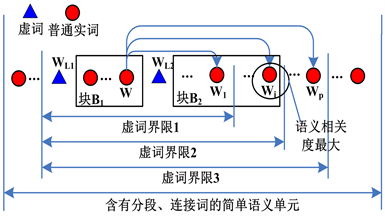
Figure 2. The processing method of the function words with segmented function
图2. 分段功能的虚词的处理方法
先将B1、B2当作两个简单语义单元处理;然后,再把WL1 B1WL2 B2的当作一个整体,用词汇W来替代即可。
2.4. 简单语义单元的语义修饰关系图模型
2.4.1. 简单语义单元的语义修饰关系图
自然语言语句中的词汇,大多数都是多义词,对简单语义单元来说,只要构造出它的语义修饰关系图,就求出了它的语法、语义分析结果,并实现了语义消歧。
假设简单语义单元的词汇序列为
。L有许多不同的语法分析方案
,图3描述了它的第t语法分析方案At,多义词Wi的第j个义项是
,多义词Wp的第q个义项是
,并且义项
语义修饰于义项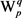 ;则在图中的义项
;则在图中的义项 和义项
和义项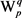 之间,画一条有向边,该边的权值等于
之间,画一条有向边,该边的权值等于 。
。

Figure 3. The graph of descriptive semantic relations for a simple semantic unit
图3. 简单语义单元的语义修饰关系图
在图3中,每个词的所有义项构成一个义项集合,每个义项都是其中的一个元素;每个词的义项集合都可以被看成一个“广义顶点”,每个义项都可以被看成一个“义项顶点”,则有如下特点:
i) 最后的词汇W0只具有一个义项,不存在语义修饰目标,其义项可以通过由语句级别处理过程确定;
ii) 每个“广义顶点”只具有一个语义修饰目标,集合的总出度是1;
iii) 每种语法分析方案,本质上都是一个语义修饰关系图,该图必然是“广义顶点完全图”的一颗“生成树”;
iv) 在任意“义项集合”中,其“生成树”的每条边,必定关联于同一个“义项顶点”。
2.4.2. 图语义修饰关系图最佳解的求解原理
自然语言语句中的词汇,大多数都是多义词,对简单语义单元来说,只要构造出它的语义修饰关系图,就求出了它的语法、语义分析结果,并实现了语义消歧。
假设某个简单语义单元,具有n种不同的语法分析方案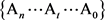 ,在它的第t语法分析方案At中,
,在它的第t语法分析方案At中, 是Wi的第j个义项,
是Wi的第j个义项,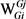 是
是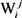 的语义修饰目标义项,
的语义修饰目标义项,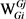 是
是 的语义修饰目标义项;用
的语义修饰目标义项;用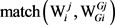 表示它们之间的语义相关度,则针对语法分析方案At,总的语义相关度fAt可以用式(2)来计算:
表示它们之间的语义相关度,则针对语法分析方案At,总的语义相关度fAt可以用式(2)来计算:
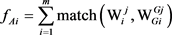 (2)
(2)
其中,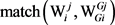 用来表示义项
用来表示义项 、
、 之间的语义相关度,针对一个词汇语义库(本文使用hownet词汇语义库),可用式(3)计算。
之间的语义相关度,针对一个词汇语义库(本文使用hownet词汇语义库),可用式(3)计算。
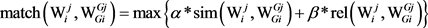 (3)
(3)
其中, 表示义原之间的最大语义相似度,
表示义原之间的最大语义相似度, 表示义原之间的最大语义关联度,且系数
表示义原之间的最大语义关联度,且系数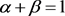 。
。
最佳解选择规则:在简单语义单元的n种不同的语法、语义分析方案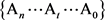 中,满足式(4)中条件的语法、语义分析方案Ai就是最佳方案:
中,满足式(4)中条件的语法、语义分析方案Ai就是最佳方案:
 (4)
(4)
最佳语法分析方案的语义修饰关系图是简单语义单元“广义顶点完全图”的“最大生成树”。
值得注意的是:代词、副词、量词、数词被按照实词计算,虚词不参与计算。
3. 语义修饰关系图模型的近似求解
假定简单语义单元具有m个词汇,一个词汇平均具有t个义项。假如采用穷举法来求取最优解,其计算复杂度将是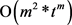 ,属于指数级别时间复杂度,实际上不可行。
,属于指数级别时间复杂度,实际上不可行。
为此,我们提出了一种近似算法,可以降低求解的计算复杂度,较快地求出近似解。
3.1. 最大生成树变量
采用动态规划方法,可以求出模型的近似解。先定义一个“最大生成树变量”(见图4),其含义为:针对词汇Wi,其第j个义项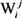 有多个生成树,其中各边权值之和最大的生成树,用
有多个生成树,其中各边权值之和最大的生成树,用 表示。
表示。
3.2. 求最大生成树的近似算法
计算过程中的所涉及的两个变量:
集合V = {已经计算出最大的生成树MT的“广义顶点”}
目标词汇Wi:即将被加入V的下一个词汇;

Figure 4. The variable of the maximum span ning tree for a simple semantic unit
图4. 简单语义单元的最大生成树变量
动态规划算法(算法1):
步骤1:设定V的初始值
设置 ,则很容易算出:
,则很容易算出:
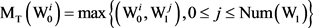 ;
;
 。
。
其中Num是词汇的义项个数,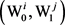 表示义项
表示义项 和
和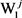 之间的边。
之间的边。
步骤2:计算目标词汇Wi的最大生成树变量
针对Wi,其每个义项 与V中的任意义项
与V中的任意义项 之间,都可以计算出一个语义相关度,按照式(5),可以计算出
之间,都可以计算出一个语义相关度,按照式(5),可以计算出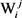 的最大生成树变量(见图5)。
的最大生成树变量(见图5)。
 (5)
(5)
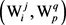 表示义项
表示义项 和
和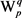 之间的边。
之间的边。

Figure 5. Computing the variable of the maximum span ning tree for semantic item 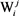
图5. 计算义项 的最大生成树变量
的最大生成树变量
步骤3:对所有的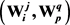 进行逆排序
进行逆排序
在步骤2的计算过程中,可以计算出所有的 的值,按由大到小的顺序,将其保存到线性表List中。
的值,按由大到小的顺序,将其保存到线性表List中。
步骤4:更新V中义项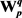 的最大生成树变量
的最大生成树变量
如图6所示,已知V中义项 的最大生成树,可定义变化函数f:
的最大生成树,可定义变化函数f:
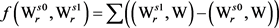 (6)
(6)
其含义为:假设把最大生成树进行一个义项改动,由义项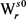 改为义项
改为义项 ,其权值之和的变化量。
,其权值之和的变化量。
假定边 所关联的顶点为
所关联的顶点为 ,把最大生成树上的义项
,把最大生成树上的义项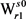 改为义项
改为义项 ;则其变化函数
;则其变化函数 的值必然小于0。
的值必然小于0。
假如按照由大到小的顺序,处理List中的所有边 ,有以下两种情况:
,有以下两种情况:
i)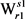 位于最大生成树上,则List中后续的任何边都不可能是最大生成树的边,因此就无需处理了。
位于最大生成树上,则List中后续的任何边都不可能是最大生成树的边,因此就无需处理了。
ii)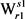 不位于最大生成树上,则按照下属算法2求取义项
不位于最大生成树上,则按照下属算法2求取义项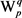 的最大生成树。
的最大生成树。
算法2:
----------------------------
For all 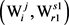 in List
in List
{
If ( 不在最大生成树上)
不在最大生成树上)
{
计算变化函数 的值;
的值;
(A) 找到 所指的下一个顶点(
所指的下一个顶点( )
)
{
针对 的所有义项
的所有义项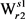 ,计算变化函数
,计算变化函数 的值;
的值;
选取能够使得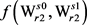 最大的义项
最大的义项 ;
;
将最大生成树的上的义项由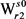 修改为
修改为 ;
;
}
返回(A),循环处理至最后一个顶点;
按下式计算总变化量:
 ,即对所有的变化函数求和,并加上边
,即对所有的变化函数求和,并加上边 的值。
的值。
}
}
选择能够使总变化量最大的边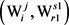 ,将其修改为最大生成树的边。
,将其修改为最大生成树的边。
---------------------------
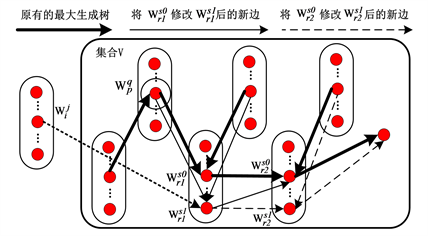
Figure 6. Updating the variable of the maximum span ning tree for semantic item 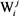
图6. 更新义项 的最大生成树变量
的最大生成树变量
步骤5:把词汇Wi加入集合V
针对V中的所有义项,更新其最大生成树变量,完成后把Wi加入集合V。
步骤6:循环
返回步骤2,循环处理,当所有顶点都加入集合V后,选出词汇Wm的最大生成树,就是所求的近似解。
3.3. 计算结果分析
在算法1的步骤4中,使用了贪心法,只选择能够使得 最大的义项
最大的义项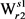 进行计算,而没有对所有
进行计算,而没有对所有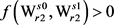 的所有义项进行穷举;故此所求的解不是“理论最优解”,只是近似解,其时间复杂度约为
的所有义项进行穷举;故此所求的解不是“理论最优解”,只是近似解,其时间复杂度约为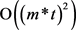 。
。
4. 实验结果及分析
实验中,以hownet作为语义计算的依据。在人民日报2014语料库中选取了1200个语句进行求解实验,先将它们转化为4729个简单语义单元,通过算法进行求解,并与正确结果进行对比。实验环境为:windows 10,i5 9400F六核,主频2.9 GHz,32 G内存。
实验情况见表1、图7、图8,其中正确率标准有两个:
1) 语义消歧正确率大于阀值0.5 (义项选择正确就是语义消歧正确);
2) 语法分析正确率大于阀值0.8 (义项的语义修饰目标正确就是语法分析正确)。

Table 1. The resulting data of experiment
表1. 实验数据表
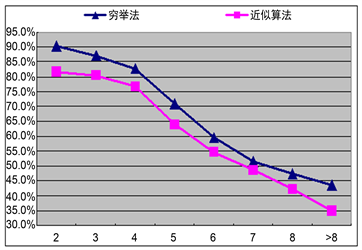
Figure 7. The comparison for the correct ratios
图7. 正确率对比图
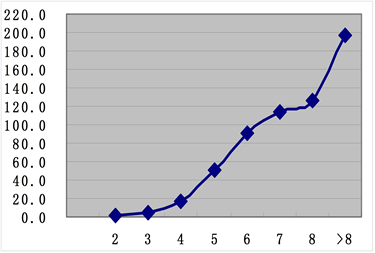
Figure 8. The exhaustive time/the approximate algorithm time
图8. 穷举法时间/近似算法时间
从实验结果可以看出:
1) 两种算法均可进行语法分析和语义消歧;
2) 穷举法的正确率略高于近似算法;
3) 正确率随着简单语义单元长度的增加有逐渐下降的趋势;
4) 当简单语义单元长度增加时,近似算法所需时间,在可接受的范围内,属于实践可行的算法,而穷举法计算所需的时间急剧增加,实践上不可行。
5. 结语
本文对简单语义单元的语义修饰关系图模型及其求解方法进行了研究;通过把语句转化为简单语义单元,生成其语义修饰关系图,通过近似算法对模型进行求解;可以实现对简单语义单元的语法分析和语义消歧;并通过实验,验证了本方法的计算效果。由于问题自身难度所限,本文没有能够找具有“非指数级别计算复杂度”的求取最佳理论解的方法。另外,在语义计算时,由于所依据的hownet词汇语义库的准确度、细致程度等有很多欠缺和不足,使得语义相关度计算结果不够准确;这也是计算效果不够理想的关键因素。这些问题,将是我们下一步的研究的目标。
基金项目
河南省教育厅科学技术研究重点项目(18A520002)。
NOTES
*通讯作者。