1. 引言
工期与成本优化属于强NP-Hard问题。一般而言,盲目地压缩工期,将使承包商投入更多的劳动力、机械和材料,从而使得建设成本的增加。如何灵活的处理两者之间的对立与统一的关系,寻求彼此间的平衡点是工程管理研究领域的热点。传统的现场施工进度优化主要依赖于人工经验,优化过程以宏观控制为主,缺乏精细化管理。施工现场的进度和成本数据主要来源于项目管理人员,技术人员负责数据的审核与纠偏。整个信息流在不同的单位,不同部门间传递缺乏有效的沟通,易产生“信息孤岛”现象;并且现场施工数据的可获取性、有效性都有待考究。施工项目工期–成本优化问题在数学上属于多元函数求最值问题,即在多约束条件下,以承包商施工成本最低为主要目标,从而解出每道施工工序的最佳持续时间 [1]。
针对上述存在的问题,国内外学者通过理论分析方法对工期与成本协同优化进行了深入的研究。其中胡长明、熊焕军等采取将BIM与挣得值法相结合的思想,最终实现工期与成本联合控制 [2]。袁振民将BIM与网络计划技术相结合,构建了系统优化体系和优化模型,最终实现进度–成本的动态协同优化 [3]。刘佳将模糊数学理论引入工期–成本优化模型中,并用混合智能启发式算法解出模型的最优值 [4] 等。以上优化方法克服了传统的静态优化模型缺陷,并采用智能启发式算法等对模型进行了快速的求解。然而,不难发现以上研究建立的模型忽略了资金的时间价值且选用的求解算法计算量大、易陷入局部最优解等问题。
BIM是将建筑物的全生命周期特征数字化表示后,以三维模型为载体,借助软件操作平台,以此来模拟与分析建筑物的真实场景 [5];为了更好的将BIM技术运用于现场实际施工,使承包商实现项目精细化与信息化管理而达到控制施工成本的目的,本文在上述文献研究的基础上,进一步分析工期与成本的内在联系,建立两者间的数学模型,并运用MATLAB2014对量子遗传算法进行编程,通过对代码的运行求解该模型。其次,将BIM技术在施工进度中的应用与基于量子遗传算法的施工进度优化体系相结合,将算法求解的优化结果输入Navisworks 2017软件中,进行现场施工全过程模拟;提前发现并解决施工过程中可能出现的问题,从而实现工程建设全过程控制。
2. 工期–费用优化理论及数学模型
2.1. 工期–费用关系
承包商的施工总成本是指项目建设过程中发生的全部费用之和,一般包括直接成本和间接成本。施工工序在项目建设中发生的所有直接费之和,称为直接成本,包括人工费、材料费、施工机械使用费等;间接成本,是相对于整个工程而言的,不易计算到每个工序中,主要包含施工管理费,冬雨季、夜间施工所增加费用,财务费 [6] 等。
工程直接成本是工期的单调递减函数,即不论以哪种方式压缩工期都会造成施工直接成本的增加;直接成本与工序作业时间之间表现为非线性关系,可以用数学拟合为二次函数形式 [7]。间接施工成本随着工期的增加而增长,缩短而降低,将其与工期简化为线性正相关关系。直接成本和间接成本相互叠加形成施工总成本。在保证工程质量与安全的前提下,项目工期–成本优化是指在建设费用最低的条件下,寻找最优施工工期 [7]。
建设资金在流动过程中所发生的时间价值可从以下两点来解析:首先,在工程建设中,费用的流动与生产与交换相互关联,整个活动过程会给出资方带来效益,具体表现为资金的升值过程。从本质上来说,就是工人从事工程建设时创造了社会剩余价值;其次,资金一旦投入到工程建设中也就而意味着放弃了资金的其他消费,因此,资金的时间价值可认为是对当前消费损失的一种补偿。资金额外增加的价值,对于资金的拥有者而言,这部分价值称为收益,对于资金借贷者来说,这部分价值称为成本。
建筑工程项目往往建设周期较长、投资额较大,资金的支付不是一次性完成,而是多时间点、多阶段化完成,这就使得建设资金的时间价值往往较大,在整个建设资金中占有较大的比例 [8]。因此,在进行工期与费用优化时不能忽略。
2.2. 工期–费用数学模型
根据以上理论分析,做出以下假设:1、不存在资源短缺而影响施工进程的情况。2、计息周期按天计算,按“利滚利”的方式计算利息。3、现场的天气状况、周边环境、劳动力数量都满足施工标准。4、完成每道施工工序的持续时间以整数计算,并小于等于正常作业时间且大于等于极限时间。通过上面的理论分析,可建立以下模型:
(1)
式中,Ci为工序i的直接费用,di(ti)为施工活动 的持续时间(开始时间),Cni(Csi)为工序i在正常作业时间(赶工作业时间)下的直接费用,tni(tsi)为工序i在正常作业时间(极限作业时间),为单位时间内的间接施工成本,∆Cfi为间接费用率。
3. 量子遗传算法求解
上述的工期–费用优化模型属于多变量、多约束、非线性的数学函数,本文采用量子遗传算法进行求解。由下图4可看出,与传统的遗传算法相比,该算法具有种群多样性好、迭代次数少、收敛速度快、全局搜索能力强、不易陷入局部最优解的特点 [9] [10]。
3.1. 量子比特编码
在经典的遗传算法中,用二进制的一个位来表示遗传信息,即“0”或“1”。但在量子遗传算法中,充当信息存储单元介质是量子比特存储和。量子比特与经典位不同就在于它除了可以以“0”态“1”态存在外还可以它们的任意的叠加和,比如:
;
、
是两个幅常数,称为量子态的概率幅,它们满足
,因此,k位二进制编码的n个参数比特编码的基因为:
(2)
式中:
代表第t代,第j个体的染色体;k为编码每一基因的量子比特数;n为染色体基因个数。由上可知,对于由m个量子比特编码的染色体可以表示2m个状态,使得量子遗传算法与传统的遗传算法相比,具备更复杂的种群。
3.2. 量子门更新
根据QGA计算特点,这里选择量子旋转门进行染色体跟新,第i位量子比特演化过程为:
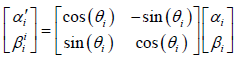 (3)
(3)
式中:
和
分别表示染色体第i个量子位更新前后的概率幅, 为旋转角,计算公式为:
,式中:
为旋转角度变化量,
为旋转角的方向,
和
的大小和符号按表1取值,表1中
为当前染色体第i位;
为当前最优染色体的第i位;该调整策略是将个体
当前的测量值的适应度
(施工成本净现值)与该种群中最优个体的适应度值
为旋转角,计算公式为:
,式中:
为旋转角度变化量,
为旋转角的方向,
和
的大小和符号按表1取值,表1中
为当前染色体第i位;
为当前最优染色体的第i位;该调整策略是将个体
当前的测量值的适应度
(施工成本净现值)与该种群中最优个体的适应度值 进行比较,如果
,则对
中相应位的量子比特进行修改,概率幅
朝着
方向进行;相反,如果
,则对
进行比较,如果
,则对
中相应位的量子比特进行修改,概率幅
朝着
方向进行;相反,如果
,则对 中相应位的量子比特进行修改,概率幅
朝着
逼近 [11]。
中相应位的量子比特进行修改,概率幅
朝着
逼近 [11]。

Table 1. Rotation angle θi strategy
表1. 旋转角θi取值策略
4. 项目优化流程
BIM技术团队通过对模型的反复模拟,提前发现模型中存在的设计、施工等问题,并反馈给相应的建设参与方进行修改,最后输出优化数据。
运用初次优化所产生的数据,进行工期–成本的二次优化分析,通过MATLAB2014计算机仿真,可得到每项施工工序的最佳作业时间与最低施工成本,并用来指导实际施工。基于量子遗传算法的BIM工期–成本协同优化过程如图1所示。
5. 实例验证
5.1. 工程概况
某地知名高校教职工公寓项目位于某市城郊20公里,总建筑面积为2340 m2,建筑高度24.0 m,共8层;采用现浇普通框架体系,采用7度抗震设防,设防类别为丙类,结构抗震等级为三级,结构安全等级为二级,耐火等级为二级;建筑外围墙和内隔墙分别为200 cm、100 cm厚的加气混凝土砌块墙。
本文根据建筑的几何尺寸、性能参数采用BIM软件中的Revit2017进行三维建模,如图2所示。
根据Revit2017生成的整个建筑工程量清单(如上图3所示),可确定第二层结构单元各工序施工持续时间,同时计算各工序的工程费用数据,如表2所示。

Table 2. Apartment main structure construction process table
表2. 公寓主体结构施工工序表
5.2. 算法应用
利用量子遗传算法能快速,高效的解决工期–费用优化问题,为现场施工管理人员提供可靠地数据参考。算法参数设定为:种群数目SIZEPOP = 50,最大遗传代数MAXGEN = 300,每个基因的量子比特数n = 20。
图4是由MATLAB2014a软件仿真得出量子遗传算法和传统遗传算法在进行工期成本优化时的最佳适应度迭代曲线。

Figure 4. Comparison of best fitness iteration curves
图4. 最佳适应度迭代曲线对比
5.3. 仿真结果分析
两种算法的仿真结果数据对比如表3所示。

Table 3. Data comparison of simulation results
表3. 仿真结果数据对比
从图4和表3可以看出,QGA求解收敛速度明显优于GA算法,在迭代10次左右即可搜索出最佳适应度,而GA算法则需150次迭代后才搜出最优解;其次,采用量子遗传算法求解得到的最低成本小于传统遗传算法,说明QGA全局搜索能力优于传统算法,有效避免了传统遗传算法易陷入局部最优的缺点。
由以上的仿真结果分析可以看出,传统遗传算法易因为交叉概率、变异概率选取不当而陷入局部收敛,并且收敛速度较慢 [12]。充分利用QGA算法染色体多样性的特点可以提高搜索空间密度,实现有效全局优化搜索,使得基于量子的遗传算法拥有收敛速度更快、精确度更高。
5.4. BIM技术模拟分析
将上述仿真结果输入Naviswork2017施工模拟软件当中,利用软件的TimeLiner功能实现工程建造过程三维模拟仿真。如图5所示。
在此过程中,项目管理人员可以实时查看项目建设的计划进度,并与实际进度进行对比;检验施工进度是否满足预定计划,如不满足,及时寻找原因并采取纠偏措施。其次,通过三维模型中所包含的施工数据,项目管理人员可以实时掌握人工、机械、材料等情况,提前安排好施工人员与机械设备等。
6. 结语
通过将BIM与优化理论相结合,本文提出了一种新的工期–成本动态优化方案。通过工期–成本理论分析,建立了工期–成本优化模型,并采用量子遗传算法求解模型,确定了在保证工程质量前提下最低成本的施工工期。运用BIM的模拟功能,以优化结果作为参考依据,可以帮助现场管理人员进行技术交底,提高承包商的项目精细化管理水平。本文提出的基于BIM的工期–成本动态优化对承包商的施工现场管理有一定的指导价值,但要实现两者间的完美结合,仍需解决两者间的接口问题。