1. 引言
二十世纪五十年代,心理学家Gibson就在他的作品中提到了环境光、环境光阵、光流、光流阵等概念 [2],可见“光流”的诸多理论很早就被提出并研究了。光流法是基于机器视觉的运动目标方法中比较主流的方法之一,相比于其他方法(背景差法、帧差法等),光流法来源于仿生学思想,它更加根本化地揭示了基于视觉的运动目标检测原理,具有更加牢固的数学基础。物理光学的概念是以能量为基础的,基于这个理论Gibson引入了生态光学理论(ecological optics theory),强调了知觉对动物在自然环境发展的重要意义。在Gibson提出了一系列的光流概念之后,便有学者提出利用二维平面的光流场来恢复三维空间运动参数和结构参数。
1976年,Pogglo和Reichartdt提出了关于光流的粗略计算形式;1981年,Horn和Schunck、Lucas提出了有效计算方法,引入了光流约束方程,对光流计算奠定了深厚基础。随后,光流被广泛运用于图像处理、目标跟踪等领域,研究人员将这些新方法分为五类 [3]:基于梯度的方法、基于匹配的方法、基于相位的方法、基频域的方法、基于神经动力学的方法。
基于梯度的方法 [4] 也叫做微分法,该类方法依赖于亮度作为常数的假设,它是利用序列图像亮度的时空梯度函数来计算二维速度场。最具代表性的是Horn-Schunck光流法(以下简称为HS光流法),它计算出的光流场是在光流基本方程的基础上引入另外一个约束条件——全局光流平滑约束,该方法计算简单效果较好,后来研究者们在HS光流法基础上做了大量改进算法。但基于梯度的光流法同样存在一些问题与缺陷,一方面是考虑到计算光流方便性时通过泰勒级数逼近来实现线性化,从而导致估计精度由于运动矢量存在较大误差而降低;另一方面是,在预处理过程中,由于部分帧数图像噪声和采集过程中的频谱混叠现象,从而影响该方法的计算精度。
基于匹配的方法 [5] 包括基于特征和基于区域两种方法,该类方法实质就是搜索图像序列中各个图像之间对应最佳拟合的位移,所得到的位移称为目标运动矢量。该类方法的优点是对目标的亮度变化和速度变化具有较强的鲁棒性,因而在视频编码中被广泛运用。基于匹配的光流法存在的问题是得到的光流通常较为稀疏,难以实现精确匹配。
基于相位的方法最先被提出用于光流计算 [6]。当计算光流的时候,图像的相位信息相比于亮度信息更加可靠,因此基于相位的方法具有更好的鲁棒性。该方法的优点是对图像序列适用的范围较宽且计算速度快,缺点是具有较高的时间复杂性且对图像序列的时间混叠比较敏感。
基于频率的方法也被称为基于能量的方法,它需要对输入的图像进行时空滤波处理从而获得均匀、流畅、精准地速度估计,也就是对时间和空间的整合。基于频率的方法缺点是涉及大量运算,并且难以做出明确的可行性分析和可靠性评价。
神经动力学方法是对生物视觉系统结构和功能较为直观的模拟,利用神经网络搭建视觉运动感知的神经动力学模型。
2. 光流法的基本原理
在我们观察二维或三维空间的目标运动时,目标的轮廓会在我们的视网膜上留下一系列连续变化的图像,这些连续变化的图像信息不断地“流过”我们的视网膜,就如同光流过一样,我们将这样的现象称为“光流(optical flow)”。在视频跟踪领域,光流在图像灰度模式的表面运动,表示物体在图像中位置的瞬时变化,是物体的三维速度矢量在成像平面上的投影 [7]。
2.1. 光流场与运动场
运动可以用运动场来描述,从而反应真实世界的三维运动。光流场是运动场在二维图像上的投影,它是一个二维矢量场,它携带了物体的结构信息和运动信息。物体在三维空间运动时会产生三维运动场,运动前后空间对应点在二维平面上投影就会形成一个二维运动场 [8]。研究光流场的实质就是实现从序列图像中近似计算出不能直接得到的运动场。图1表示三维空间运动矢量场在二维平面内的投影。

Figure 1. 3D space motion vector field and 2D space motion vector field
图1. 三维空间运动矢量场与二维空间运动矢量场
2.2. 基本光流约束方程
假设图像区域在时间和空间上都是连续可导的,那么对于一个图像序列图像中的一个像素点
在t时刻的亮度值为
,而
和
分别代表点
在处光流在x和y方向上的运动分量。在一个足够短的时间dt内,点
移动到点
,其中
,
。Horn和Schunck假定亮度恒定,即沿某运动轨迹曲线的各帧对应像素点具有相同灰度值,可以得到:
按一阶泰勒公式展开:
抵消
,得到:
这是基本光流约束方程,可以看到基本约束方程中有两个未知数,这种情况下无法求得u,v的值,因此需要增加其它约束。从不同角度引入约束条件就会生成不同的光流计算方法,按照文章引言部分的介绍可以将计算分为五种方法,方法的背景理论此处不再赘述。
2.3. 光流法的优劣
光流法最显著的优势是可以在摄像机运动的情形下实现运动目标的检测和跟踪,而且比帧差法、背景减法、光流法具有更高的准确率,甚至可以直接计算得到目标物体的运动参数,解决传统的基于目标特征的运动检测难以克服的遮挡问题。但是,光流法鲁棒性与实时性欠佳,计算相对比较复杂,且抗干扰能力差。
由于光流法依赖于采取假设的局限性,使得光流法对光源的变化十分明显,再加上阴影、噪声等方面的影响,很容易产生错误的结果,因此光流法难以满足实时性需求。不过,在现有的算法基础上,搭建基本的系统框架,解决可以满足假设条件的问题是十分可行的。如何提高光流法的抗噪性和实用性是需要我们进一步研究的课题。
3. HS光流法
Horn-Schunck光流法是在光照强度不变的假设条件下 [9] [10],引入了全局光流平滑约束。假设物体运动矢量是平滑的或是缓慢变化的,即整个图像上的光流变化是平滑的,相邻像素点间的速度变化是相同的。Horn与Schunck引入光流基本约束方程和全局光流平滑约束来计算V,由于图像相邻像素点间的运动速度相同,因此速度的空间变化率为0,而得到光流矢量约等于0。对于图像的局部区域来说,引入光流平滑约束的的基本前提就是光流要尽可能的平滑,使得平滑约束项极小化。
根据光流基本约束方程,将光流误差
进行极小化:
于是对光流场的求解便转化为对如下问题的解:
印章在预处理之后的两帧图像满足亮度分量恒定这一条件,因此引入全局光流平滑约束来作为第二个约束条件。在第二章详细介绍了待识别印章与参考印章的归一化操作,则直接输入两幅灰度图像进行迭代来计算速度场:
上式采用变分运算,根据欧拉方程:
得到:
式中,拉普拉斯算子可用某一点的速度与其周围速度平均值之差来近似:
化简上面两个式子:
迭代求解,对于u和v,采用九点差分格式:
而对于其中的灰度梯度,可用下面公式近似计算:
至此,输入两帧灰度(二值)图像进行迭代运算便可得到速度场。
4. HS光流算法实验
HS光流算法的执行步骤总结如下:
1) 读取待识别图像与参考图像数据并初始化矩阵;
2) 初始化迭代参数、平滑约束权重系数;
3) 计算灰度梯度
、
、
,进行微分;
4) 计算
次速度平均值;
5) 计算k次迭代的速度值;
6) 计算两次迭代的光流值误差,若小于给定误差值域则计算结束,否则进行
次迭代。
输入形态学处理过后的两帧待识别印章图像(图2(a))和存档图像(图2(b)):
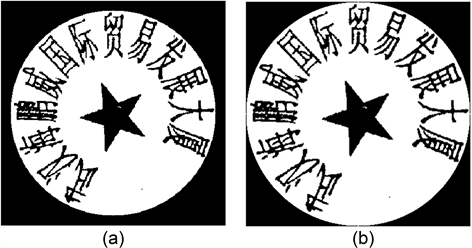
Figure 2. (a) Binary image of the stamp to be identified after morphological processing; (b) Binary image of archive stamp after morphological processing
图2. (a) 形态学处理后的待识别印章二值图像;(b) 形态学处理后的存档印章二值图像
图3展示了图2(a)和图2(b)的HS光流运动矢量场结果图:
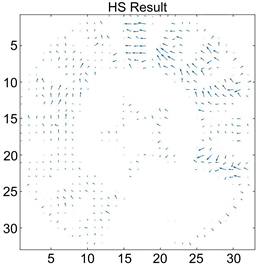
Figure 3. HS optical flow motion vector field
图3. HS光流运动矢量场
得到HS光流法结果图之后,将光流场分为16个区域计算区间矢量方差。假设区间方差表示为
,根据经验设定区间方差阈值Th后将
分别与Th进行对比。方差计数器count置为0后不断将有效区间方差进行累加,当区间方差
时,count累加1,直到16个区间全部比较完毕:
而对于每一个区块,再将之细分为4 * 4个区块,计算每个区块的区间方差,分块效果示意可见图4,而对于比较结果分为三种情况,总结至表1。

Table 1. Schematic classification of interval variance comparison results
表1. 区间方差比较结果分类示意图
以每个大区域为单位,计算16个大区域中各自分块的适配比例,并重累加计数器P、L的值,直到分块计算完毕。
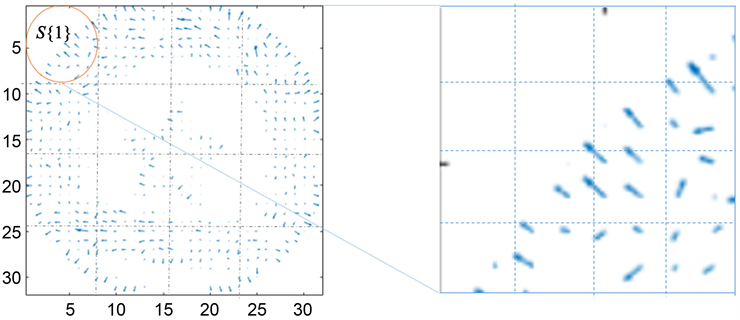
Figure 4. Optical flow field blocking effect diagram
图4. HS光流场分块效果示意图
加入判定指数:
最终判定条件:
这里选择经验阈值
为70,当
时,HS光流法匹配通过,否则匹配不通过。
5. 结论
引入Horn-Schunck光流运动矢量法目的是计算旋转达到一致性的留档印章图像与待识别印章图像的像素速度矢量,从而判断二者的匹配度是否达到经验阈值。选择精确的经验阈值是HS光流法能否正确判断的重点,值得注意的是,经验阈值需要在大量数据实验的基础上给出,在满足通过率的前提下找出区分真伪印章的最佳经验阈值是研究的难点所在。