城市快速路网交通拥挤水平的非线性模糊综合评价研究

An Improved Non-Linear Fuzzy Comprehensive Method for Assessing Urban Freeway Network Traffic Congestion Level

摘要: 快速路网交通拥挤监测和评价对于制定交通拥挤管理与控制策略有重要意义。而现有的评价研究中没有很好地把评价者主观判断偏好和指标自身影响重要度两方面因素的作用区分开来，并统一考虑在评价方法里。因此，本文首先提出了城市快速路网交通拥挤指标体系，并通过引入主观偏好参数和指标客观影响重要度参数改进了非线性模糊综合评价方法来解决现有研究的不足，使得改进的方法能反映主客观权重对评价结果的作用。最后针对上海市快速路网交通拥挤评价实例对比了传统线性模糊综合评价方法、非线性模糊综合评价方法和改进的非线性模糊综合评价方法的评价结果的异同。研究发现改进的方法评价结果更加符合实际情况，稳定性也更好。

Abstract: The monitoring and evaluation of traffic congestion on urban freeway network is of great significance for the formulation of traffic congestion management and control strategies, one improved non-linear fuzzy comprehensive evaluation methodology (iNFCM) is proposed for urban freeway network traffic congestion assessment, which manages to highlight both the effect of judgment preference and the effect of influencing importance by incorporating new parameters. The data-driven whole assessment process consists of two sequential stages: one being calculation of network-level traffic congestion indicators; the other one being determination of network traffic congestion level. Finally, the proposed methodology, as well as traditional fuzzy comprehensive evaluation method (tFCM) and nonlinear fuzzy comprehensive method (NFCM), are applied using Shanghai urban freeway network traffic flow data collected on 2013/02/05. It is found that the exactness and stability of results obtained by iNFCM are better than those given by the other two methods.

1. 引言

为了缓解日益严重的城市交通拥挤，越来越多的大城市开始建设城市快速路系统。这种实践证明，快速路能以较少的道路资源承担较多的交通量，具有更高的交通运输效率，确实改善了城市交通。以上海市为例，快速路道路面积只占整个城市路网道路面积的5%，却承担了30%的日交通流量 [1]；另外北京市的快速路里程占城市道路总里程的8%，却承载了50%的交通流量 [2]。与此同时，快速路的交通拥挤也日趋严重，如何通过交通管理与控制确保快速路的交通运行通畅安全便越发重要了。而交通状态及态势评价是交通管理与控制的基础和前提。尽管路段交通拥挤评价研究取得了丰富的成果，但实时准确地评估路网交通拥挤水平研究仍缺乏深入讨论，造成目前对快速路交通管控实时全局优化指导性不强的局面。

交通拥挤指标和评价方法是交通拥挤评价研究中重要的两个内容。由于交通拥挤评价是一个多层次多角度多指标的综合评价，所以至今还未形成一个普遍接受的评价指标和评价方法。本文所指的快速路网是由上匝道–主线路段–下匝道为基本单元的多条快速路连通构成的整体路网，属于宏观层面的评价问题。一方面，由于快速路与公路，特别是高速公路在道路条件、车流构成、管控手段上有相似之处，所以比较成熟的公路网交通拥挤评价最新研究成果 [3] [4] 也为快速路网交通拥挤评价提供了参考。另一方面，快速路交通状态易受到地面道路网络拥挤传播的相互影响，所以在评价时要兼顾网络拥挤特征。在城市路网拥挤指标研究方面，罗蓓蓓在研究拥挤管理系统(CMS)时提出了由拥挤持久度、拥挤影响度、行程时间波动度三个要素构成的拥挤评价综合指标；指标权重采用了AHP获得 [5]。钟秀提出了路网平均速度和路网拥堵路段比例两个指标，并给出了每个指标在不同等级拥挤的临界值 [6]。李晓丹等使用浮动车数据计算了路段拥堵持续时间、区域行程时间延误和区域拥堵路段数量三个指标，来量化城市地面路网交通拥堵状态的时空演化 [7]。任其亮提出了两级指标体系，并使用模糊层次评价法进行了评价。其中一级指标包含交叉口交通拥挤度和路段交通拥挤度，二级指标细化为交叉口排队长度、交叉口一次停车率、交叉口饱和度、交叉口延误、路段饱和度、路段延误、路段占有率和路段速度等指标 [8]。另外北京、上海、广州等城市的交通管理部门都相应制订了各自的交通拥挤评价标准和交通拥挤指数 [9] [10] [11]。他们的做法是通过车速判断路段拥挤等级，然后使用交通量相关的指标进行加权集计运算，形成一个定性结果。可以看出这些指标大部分是针对城市地面路网；交通拥挤指数可以应用于城市地面路网和快速路路网；现有指标对于快速路网拥挤评价来说要么不适用要么过于简单，决策者主观意愿也没有得到体现。

当路网交通拥挤指标不少于2个时，通常要集成一个更综合指标或指数。现有研究中加权线性求和以及模糊综合评价方法是最为流行和采用的，因为他们简单直观，便于实施。由于交通拥挤是一个模糊量，使用指标区间定义拥挤比单值定义会更符合实际，所以采用模糊综合评价的方法更恰当。尽管研究者各自使用的路网指标不同，但是这些模糊综合评价方法都归于传统的线性模糊综合评价一类 [12] [13] [14] [15]，最大的缺陷是采用线性运算不能准确考虑某个指标的突出影响和重要程度。另外对于各指标的权重确定或者只考虑了主观权重，或者只考虑了指标本身所携带的信息，并没有综合考虑两者。非线性模糊综合评价方法能弥补传统线性模糊综合评价方法的不足，并且成功应用于水质评价、石油开发规划评价等问题 [16] [17]。目前并没有发现非线性模糊综合评价方法应用于交通拥挤评价研究中。由于交通拥挤评价是需要同时考虑人的主观判断和交通流指标自身变化程度两个方面，因此在本文中分别用主观权重和客观权重来表达并引入到传统的非线性模糊综合评价方法里，形成了改进的非线性模糊综合评价方法。该方法能把评价者主观判断偏好和指标自身影响重要度两方面因素的作用区分开来，并统一考虑在评价方法里。另外“自下而上”地设计了适合快速路网运行特征的拥挤指标评价体系。最后基于上海市快速路上布设的双线圈环形检测器采集的交通流数据验证了本方法的可行性和有效性。

2. 快速路网交通拥挤指标体系构建

2.1. 快速路网交通拥挤评价指标选择

快速路是一种连续流交通设施，其运行特征可以通过连续交通流指标，比如交通量、车速、占有率等来反映。这些指标可以通过环形线圈、微波等检测器直接得到。因此基于路段车速的路段交通拥挤判断是比较容易实现的。关于快速路路段拥挤阈值研究方面：在上海，严重交通拥挤、轻微拥挤和畅通的车速指标阈值分别是20 km/h，35 km/h [6]。在北京，路段拥挤等级分为5级，从畅通级别到严重拥挤级别用1到5表示，其四个阈值为65 km/h，50 km/h，35 km/h和20 km/h [9]。参考现有研究成果，路段拥挤等级按照以上四个阈值分为1~5级，级数越大说明越拥挤。现在最大的困难是如何通过路段交通拥挤状态得到整个路网的交通拥挤状态。路段交通拥挤评价与路网交通拥挤评价是不同的，前者只是针对单一路段断面，后者针对多个路段断面，同时考虑不同路段之间在交通量和路段长度等因素差异。本研究的路段是指快速路主线上的基本路段。基本路段指的是快速路车行道不受出入口合流、分流、交织车流影响的路段 [18]。基本路段长度显然要小于其上下游的匝道的间距。结合上海市的匝道设置和实际线圈布设距离测算，本文使用的基本路段平均长度约为1.9 km，长度以1~4 km内的路段占较大比例。

本研究认为快速路网交通拥挤评价应从拥挤程度、空间范围以及时间范围三个维度入手，分别用路网平均车速、拥挤路段里程比例和拥挤持续时间比例表示，然后借助多指标综合评价方法形成一个综合直观的评价结果。在考虑数据获取可行性的基础上设计了城市快速路网交通拥挤指标体系，如图1所示。这些指标均可以通过实时采集的线圈数据集计算得到，因而结合简单高效的评价方法可以用于实时拥挤评价。

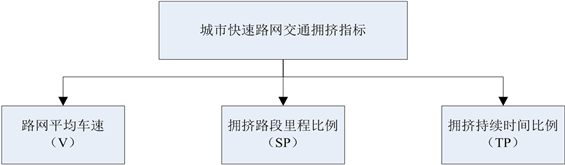
Figure 1. Urban freeway network traffic congestion indicator system

图1. 快速路网交通拥挤指标体系

2.2. 各指标定义及计算

下面以主线路段的三个指标定义及计算为例说明如何利用环形线圈检测的路段交通流数据得到路网评价指标。

路网平均车速V是评价时长内所有主线路段的行程车速的加权值。行程车速可以由线圈检测器输出的时间平均车速转换得到。权重以各路段的交通量确定，如下式所示。

式中： $V_j^k$ ：k时段内路段j平均车速(km/h)；时段可以根据线圈采集数据间隔确定，20 s~5 min不等。这里使用5 min作为一个时段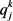；：k时段内路段j的流量(pcu/5 min)；K：评价时长，用包含的时段个数表示，通常1个小时，即K = 12； $A$ ：路网中主线路段集合。

主线拥挤路段里程比例SP是所有小于35 km/h的主线路段里程之和与主线总里程之和的比值。即选取的路段是拥挤水平处于4级或5级的路段。

$SP=\frac{1}{K}{\displaystyle \underset{k=1}{\overset{K}{\sum }}{\displaystyle \underset{i\in I}{\sum }ws{p}_i\ast S{P}_i^k}}$

$S{P}_i^k=\frac{{\displaystyle \underset{j\in A_l^k}{\sum }{l}_j}}{{\displaystyle \underset{j\in A}{\sum }{l}_j}}$

式中：I：是路段拥挤水平等级(1~5)； $A_i^k$ ：k时段内处于i级拥挤水平的路段集合； $ws{p}_i$ ：是i级拥挤里程比例 $S{P}_i^k$ 的权重，如果 $i\ge 4$， $ws{p}_i=1$ ；如果 $i<4$， $ws{p}_i=0$ ； $l_j$ ：路段j的长度(km)。

主线的拥挤持续时间比例TP是所有小于35 km/h的主线路段持续时间(时段数)与所有主线路段的评价时长时间之和的比值。

$TP=\frac{1}{K}{\displaystyle \underset{k=1}{\overset{K}{\sum }}{\displaystyle \underset{i\in I}{\sum }wt{p}_i\ast T{P}_i^k}}$

$T{P}_i^k=\frac{{\displaystyle \underset{j\in A_i^k}{\sum }{\delta }_j^{i,k}}}{{\displaystyle \underset{i}{\sum }{\displaystyle \underset{j\in A_i^k}{\sum }{\delta }_j^{i,k}}}}$

式中： $wt{p}_i$ ：是i级拥挤持续时间比例 $T{P}_i^k$ 的权重，如果 $i\ge 4$， $wt{p}_i=1$ ；如果 $i<4$， $wt{p}_i=0$ ； ${\delta }_j^{i,k}$ ：0~1变量，如果路段j属于i拥挤等级路段集合 $A_i^k$，即 $j\in A_i^k$，则 ${\delta }_j^{i,k}=1$，否则 ${\delta }_j^{i,k}=0$。其他变量含义同上。

3. 快速路网拥挤水平的非线性模糊综合评价方法

非线性模糊综合评价方法是在线性模糊综合评价方法的基础上通过引入新的参数和合成算子而形成的。其基本原理如下：假设评价指标集为 $U=\left\{u_1,u_2,\cdots ,u_n\right\}$，共有n个指标。每个指标的等级分为m级，则评价等级论域为 $V=\left\{v_1,v_2,\cdots ,v_m\right\}$，那么对于某个具体评价对象P，都将对应一个模糊关系矩阵 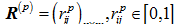。它表示了评价对象P的每个指标u对各评价等级v的隶属度。另外假设各指标的权重为 $A=\left(a_1,a_2,\cdots ,a_n\right)$，那么传统的线性模糊综合评价结果就可以在一定的标准下根据运算 $B=A\cdot R=\left(b_1,b_2,\cdots ,b_m\right)$ 得到。但是这种处理在评价结果中不能完全体现出各指标的影响重要程度。因此张晓慧等提出了一个非线性的模糊矩阵合成算子 [19]：

$f\left(A;X;\Lambda \right)={\left(a_1{x}_1^{{\lambda }_1}+a_2{x}_2^{{\lambda }_2}+\cdots +a_n{x}_n^{{\lambda }_n}\right)}^{\frac{1}{\lambda }}$

式中： ${\lambda }_i$ 反映了指标的突出影响重要度，其值越大说明指标越重要；

${\lambda }_i\ge 1,i=1,2,\cdots ,n$

$\Lambda =\left({\lambda }_1,\lambda {}_2,\cdots ,{\lambda }_n\right)$

$\lambda =\max \left\{{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n\right\}$

$A=\left(a_1,a_2,\cdots ,a_n\right);a_i>0,i=1,2,\cdots ,n$

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{a}_i}=1$

$X=\left(x_1,x_2,\cdots ,x_n\right);x_i\ge 1,i=1,2,\cdots ,n$

使用这个算子进行运算，可以得到评价结果对应于不同等级的隶属度值，根据最大隶属度原则，可以确定相应的交通拥挤水平。在实际应用中，为了使 $X\ge 1$，通常做法是令 $X={\text{e}}^R$ 或者 $X=2^R$， $R$ 是隶属度矩阵。而突出影响重要度向量 $\lambda$ 根据指标分类结合主观评价的矩阵A来确定，通常做法事先设置不

同等级的影响重要度 ${\lambda }^{\left(k\right)}$，并令 ${\lambda }_i={\lambda }^{\left(k\right)}$ [17]，或者 ${\lambda }_i=\frac{a_i}{\min \left\{a_i\right\}}$ [19]。这里可以反映出非线性模糊综合

评估中基于主观权重的指标影响重要度信息。另一方面，本文同时使用基于实际数据分布的熵值法来确定指标的客观权重，以及采用上述相同处理的基于客观权重的指标影响重要度信息。本文所做的方法改进即是把主观权重及基于客观权重的影响重要度综合考虑并统一应用到传统非线性模糊综合评价方法中。

关于隶属度的确定，这里采用三角函数的形式，每个指标等级阈值如表1所示，其中车速阈值采用了现有的上海 [6] 和北京成果 [9]；拥挤路段里程比例(SP)和拥挤持续时间比例(TP)是在参考上海市路网拥挤判定比例的基础上按等比例分配得到 [4]。最终路网交通拥挤等级分为1~5级，1~5分别表示非常畅通、畅通、轻微拥挤、严重拥挤和极度拥挤。

Table 1. Each indicator interval under different congestion levels

表1. 不同拥挤等级下各指标区间划分

关于主观权重的确定，可以根据采用常见的Delphi法，AHP法等，在此不再赘述。需要说明的是，指标主观权重是随着应用环境的变化而变化的，比如在高峰时段或非高峰时段，正常天气或恶劣天气条件下评价者可能对不同指标的重视程度不一样而得到不同的权重。

4. 实例应用与分析

上海城市快速路网自二十年前开始规划建设，现在已经比较完善和发达。上海快速路网络主要由中环、内环、南北高架和延安高架组成，呈“申”字形。限于实际交通流数据的获取情况，在本研究中选择了中环、内环和南北高架三条主要快速路作为一个子路网整体分析，如图2深颜色所示。道路路段的长度等信息通过shape文件的属性表得到。时间间隔为5分钟的环形线圈数据作为主要交通流数据来源，包括了车速、流量、占有率等信息。

Figure 2. Shanghai urban freeway network

图2. 上海市快速路网

在现有线圈布设基础上将研究子路网共划分为182个基本路段(双向)，其中南北高架40个，平均长度为1.34 km；内环高架66个，平均长度为2.05 km；中环高架76个，平均长度为2.09 km。数据采集时间段是2013/02/05 (周二) 5:00 am~5:00 pm。分析时段间隔是1小时，共有12个小时。在各基本路段5分钟的原始交通流数据基础上，利用sql server 2005的SQL语言编程实现了2.2节三个指标的计算，获得了每小时的交通路网拥挤各指标，如表2所示。

Table 2. The time-varying condition of traffic congestion index of the road network

表2. 路网交通拥挤指标时变情况

根据表2的结果，利用熵值法可以得到客观权重及影响重要度。同时主观权重A根据专家打分法得到。传统的非线性模糊综合评价的影响重要度是根据主观权重确定，如表3第五列。改进的非线性模糊综合评价的影响重要度是根据客观权重确定，如表3第三列。在下文计算中，传统的线性模糊综合评价只使用了主观权重A，传统的非线性模糊综合评价使用了主观权重A及影响重要度2，改进的非线性模糊综合评价使用了主观权重A及影响重要度1。

Table 3. Subjective and objective weight and influence importance

表3. 主客观权重及影响重要度

速度的隶属度函数如图3和下列公式所示。限于篇幅，其他两个指标的隶属度函数在此省略。在分别确定了各指标的隶属度三角图示及隶属度分段函数后，就可以进行模糊综合评价。逆模糊过程是根据最大隶属度原则确定。

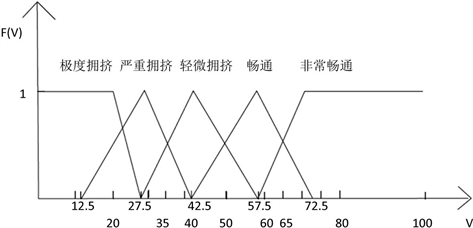
Figure 3. Membership function of velocity

图3. 速度的隶属度函数

$u_5\left(V\right)=\{\begin{array}{l}1,V<20\\ 1-\frac{V-20}{7.5},20<V<27.5\\ 0,V\ge 27.5\end{array}$

$u_3\left(V\right)=\{\begin{array}{l}0,V<27.5\\ \frac{V-27.5}{15},27.5<V<42.5\\ 1-\frac{V-42.5}{15},42.5<V<57.5\\ 0,V\ge 57.5\end{array}$

$u_2\left(V\right)=\{\begin{array}{l}0,V<42.5\\ \frac{V-42.5}{15},42.5<V<57.5\\ 1-\frac{V-57.5}{15},57.5<V<72.5\\ 0,V\ge 72.5\end{array}$

$u_1\left(V\right)=\{\begin{array}{l}0,V<57.5\\ \frac{V-57.5}{7.5},57.5<V<72.5\\ 1,V\ge 72.5\end{array}$

按照以上步骤对7:00~8:00的路网交通拥挤等级进行评级，过程如下：

由表2得到：

$\left[\begin{array}{ccc}V& SP& TP\end{array}\right]=\left[\begin{array}{ccc}56.4& 10.25\%& 9.67\%\end{array}\right]$

根据三个指标各自的隶属度函数计算得到， $R=\left[\begin{array}{ccccc}0& 0.9239& 0.0761& 0& 0\\ 0.0245& 0.5123& 0& 0& 0\\ 1& 0.4834& 0& 0& 0\end{array}\right]$

对矩阵R取指数运算，得到

$X={\text{e}}^R=\left[\begin{array}{ccccc}1& 2.5191& 1.0791& 1& 1\\ 1.0249& 1.6691& 1& 1& 1\\ 2.7183& 1.6216& 1& 1& 1\end{array}\right]$

基于表2的所有数据使用熵值法计算得到表3的客观权重及指标重要度 $\Lambda =\left[\begin{array}{ccc}1& 3& 3\end{array}\right]$， $\lambda =3$。同时表3也给出了主观权重 $A=\left[\begin{array}{ccc}0.7& 0.2& 0.1\end{array}\right]$。

根据非线性模糊算子计算得到： $B=f\left(A,X,\Lambda \right)=\left[\begin{array}{ccccc}1.3345& 1.5312& 1.0230& 1& 1\end{array}\right]$，因此根据最大隶属度原则，对应的交通拥挤等级为2级。

为了说明改进的非线性模糊综合评价方法(iNFCM方法)的有效性，对传统线性模糊综合评价方法(tFCM方法)、以及非线性模糊综合评价方法(NFCM方法)也一并使用Matlab编程实现，其结果如表4所示。

Table 4. The evaluation results of congestion level under different methods

表4. 不同方法下拥挤水平评价结果

可以看出在传统线性模糊综合评价方法与传统的非线性评估方法由于只考虑了主观权重，评价结果都有3种拥挤水平，而改进的iNFCM只有2种拥挤水平。最近基于MFD (macroscopic fundamental diagram)的宏观路网交通状态识别方法被认为是一种较好实用价值的准确度较高的方法。参考文献 [20] [21] [22] 的做法，建立了研究子路网的宏观基本图，如图4和图5。从中可以看出，交通状态只有两个水平，另外这两个水平明显位于最大平均流量的左侧，属于不拥挤区域。

Figure 4. Road network average flow-average density diagram

图4. 路网平均流量–平均密度关系图

Figure 5. Average flow-average density of the road network after the upper limit of the coordinate axis is extended to the standard range

图5. 坐标轴上限扩大到标准范围后的路网平均流量–平均密度关系图

出现差别的原因是前两种方法过分强调了速度指标，在10~11点和14~15点两个时间段判定为轻微拥挤，而改进的非线性模糊综合评价方法很好地结合了主客观权重的影响，得到的结果也更稳定可信。

5. 结论

本文主要研究结论有：1) 基于高密度分布线圈检测数据可以用于建立城市快速路路网交通拥挤指标体系；2) 使用专家打分法和熵值法分别确定了评价主客观权重影响，整合提出了考虑主客观权重的非线性模糊综合评价模型；3) 利用上海市快速路局部路网验证了本文改进的评价方法评价结果更加符合实际情况，稳定性也更好。尽管本文研究了快速路网交通拥挤实时评价方法，但是方法也可分析单条快速路。下一步需要在更大路网更加拥挤状态下进行验证，进一步确定路网不同拥挤水平合理阈值。另外关于路段重要度以及上下匝道交通运行的影响也是路网交通拥挤未来研究需要解决的问题。

基金项目

山东理工大学校级博士科研启动项目(4033/719001)。