1. 引言
随着国内经济持续不断的发展,乘坐高铁出行越来越受到大众的欢迎。高铁车站服务水平,也越来越受制于车站检票匝机的工作效率。高铁车站检票时间一般为10 min,在有限的10 min内需要引导乘客完成过匝排队、检票过闸、登车等一系列乘车行为,检票闸机口区域成了车站旅客服务的瓶颈区域 [1] [2] [3]。研究旅客的过闸行为,对提高检票系统的效率具有重要的现实意义。目前元胞自动机模型、磁场力模型、排队模型、社会力模型和气体动力学模型是研究行人流最为流行的五种模型,其中元胞自动机模型和社会力模型应用最为广泛。Dirk Helbing在流体动力学方程的基础上,从微观层面上提出了第一个具有深远影响的模型——社会力模型 [4],自身前向的驱动力,行人之间的相互作用力,以及行人与边界之间的作用力是该模型的三个主要作用力。利用社会力模型对各项力进行量化分析,可以从微观层面上研究不同环境下,尤其是拥堵环境行人步行速度和行人交通流量间的运动规律。国内学者刘明姝、张国宝运用排队论和仿真分析,提出了车站自动检票闸机的布局方案,并将仿真分析结论用于客运服务设备配置研究 [5]。覃松涛 [6] 和翟向荣 [7] 对过闸行人调查数据进行分析,最终总结了影响旅客通过检票闸机时间的几个重要因素分别为性别、年龄、对闸机操作流程的熟练度、携带行李的大小和提高过匝效率的措施。论文第1章介绍一般的社会力模型,第2章根据行人特点,建立了乘客自主过闸的社会力模型,第3章主要介绍实验观测过程和参数校正,第4章呈示了模型仿真结果,第5章为模型的检验,最后给出了本文的主要结论。
2. 传统社会力模型
社会力模型中有三种不同作用力:前向自驱动力、行人间的作用力、人与边界(墙壁、障碍物等)之间的作用力,这些力的合力作用于行人,并最终驱使行人达到最终目的地 [8]。本文选取社会力模型作为乘客过闸行为研究模型。传统社会力模型中行人受力情况如图1所示。

Figure 1. Traditional pedestrian stress diagram
图1. 传统行人受力示意图
(1)
(2)
其中
为行人
的总社会力,其表达式右侧第一项为驱动力、第二项为行人与其他行人作用力的合力、第三项为行人与边界或障碍物作用力的合力,
为随机变量。
驱动力是行人主观意识对个体行为的影响,可以说是行人对自己施加的“力量”。这种驱动力驱使行人选择正确的路径到达最终目的地,省略误差项可以把公式(1)改写成公式(3):
(3)
其中,
为 行人期望的运动方向,一般与人前进方向相同,  为行人的期望速率;
为行人的即时行走速度,
为行人反应时间,也称松弛时间。
为行人的期望速率;
为行人的即时行走速度,
为行人反应时间,也称松弛时间。
行人与行人之间的作用力主要包括2个部分的力:“社会心理力”
和“身体接触力”
。行人之间的距离越小,作用力越大,但不会超过一个最大值,随着行人之间距离的增大,作用力逐渐减小到0。如下列公式所示:
(4)
障碍物或边界对行人产生的作用力与行人之间的作用力相似,障碍物或边界对乘客产生的作用力可以同样可以分为“社会心理力”和“身体接触力”两种,如公式(5)所示:
。 (5)
3. 乘客自主过闸社会力模型
本文将闸机看作是一个具有“粘性”的、会与乘客发生作用关系的物体,乘客年龄、携带的行李类型、对闸机操作的熟练度都会对乘客过闸效率产生影响,乘客过闸受力如图2所示。
图中:
(6)
(7)

Figure 2. Schematic diagram of the force when the passenger passes the gate
图2. 乘客过闸时受力示意图
其中,
表示闸机对乘客
的作用力;
表示
的驱动力;
为其他行人对
的作用力,
表示闸机对过闸乘客的作用力, 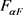 为乘客对过闸操作熟练度产生的作用力,
为闸机边界“粘性”对乘客产生的阻碍力,
表示闸机边界对行李产生的阻碍力,
为修正系数。
为乘客对过闸操作熟练度产生的作用力,
为闸机边界“粘性”对乘客产生的阻碍力,
表示闸机边界对行李产生的阻碍力,
为修正系数。
3.1. 小件行李乘客过闸社会力模型
携带小件行李乘客过闸时所受的作用力为其他行人的作用力以及闸机对乘客的作用力,如公式(8)~(9)所示:
(8)
(9)
在公式(8)中,
表示小件行李乘客过闸的社会力;
表示小件行李乘客的驱动力,
为其他行人对小件行李乘客的作用力;
为闸机边界对乘客产生的阻碍力,
为随机干扰项。
3.2. 中大件行李乘客过闸社会力模型
与小件行李乘客相比,在分析中大件行李乘客过闸社会力时,需要分析行李与闸机边界之间的作用力,影响中大件行李乘客过闸速度的因素主要有行李的重量和体积,行李的重量因素可以附加到乘客本身的质量进行考虑,因此需要分析行李尺寸对过闸速度的影响,与乘客与障碍物之间的作用相似,只是行李作为物体,少了一个与障碍物之间的“社会心理力”,因此行李与障碍物之间的作用力主要为“身体接触力”,公式如下所示:
(10)
(11)
其中,
为障碍物到行李中心的距离;
为行李边界与障碍物之间的距离;
为行李相对于闸机的速度,因此行李的速度即为乘客的速度,所以
;
为为示性函数,行人间存在接触时取1,未接触取0;k为行人
的斥力参数,一般为定值;
为行人
的摩擦力参数,一般为定值。
3.3. 老年乘客过闸社会力模型
老年人体力不如中青年人,因此选择乘坐高铁进行远距离出行人数较少,即使出行,也会携带较少或者不携带行李,所以老年乘客过闸受力与小件行李乘客社会力模型一样
。 (12)
4. 实验数据及参数校核
4.1. 样本概况与预处理
利用视频分析软件,通过对长沙南站2017年10月份期间部分时段摄影机记录的B8、B9、B12、B13检票口乘客过闸机影像进行分析研究,在剔除乘客年龄段分布不明显等特殊样本后,本文总共收集728组可用数据,乘客按照年龄分为:18~60岁之间乘客(将其定义为中青年乘客)、60岁以上乘客(将其定义为老年乘客)两大类;按过闸时乘客属性分为:携带中大件行李乘客、携带小件行李乘客以及检票不顺畅乘客三类。乘客过闸行为的调查样本概况如表1所示。

Table 1. Pedestrian crossing behavior survey sample summary table
表1. 行人过闸行为调查样本概况表
4.2. 乘客过闸时间分析
乘客在单位时间内在闸机通道内通过的距离即为乘客过闸时的速度,它时描述乘客过闸时效率的基本参数,单位一般为是m/s。在闸机通道宽度与长度一定时,乘客过闸时间便是反应乘客过闸速度的指标。
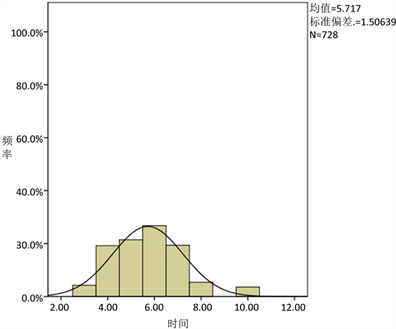
Figure 3. Passenger crossing time distribution map
图3. 乘客过闸时间分布图
对每个乘客的过闸时间进行分析与统计,从而得出总体乘客的过闸时间。对离散型的过闸时间分布,可以用统计方法来描述,即用平均值或代表性的数值来衡量总体乘客过闸时间的分布 [9]。根据实际调查数据,乘客过闸是时间直方图分布如图3所示。
对调查数据分类研究发现,乘客过闸时间主要与是否携带行李、乘客年龄层以及对闸机的熟练程度有关,与乘客性别关系不大。通过自主过闸的乘客数据类型可以发现中大件行李乘客数:小件行李乘客数:老年乘客数:检票不顺畅乘客数约为10:20:1:2。调查发现行李尺寸越大,过闸速度越慢,老年人及小孩子相对青年及中年人过闸速度较慢,延误情况大多出在老年乘客身上,四类乘客过闸平均时间如表2所示。

Table 2. Distribution of different types of passengers
表2. 不同类型的过闸乘客人数分布
4.3. 参数校正中关键指标获取
在社会力模型中,乘客通过速度是最为关键的指标,因此需用乘客通过闸机的速度来描述乘客过闸的期望速度。根据调查所统计出的数据求得,在通过2 m闸机通道时,利用公式
,即可求得每个乘客过闸速度。通过计算分析分别得到中小件行李乘客、大件行李、老年乘客过闸期望速度区间如表3所示。

Table 3. Different types of passenger speed expectation zone
表3. 不同类型的过闸乘客速度区间
4.4. 最优参数确定
本文根据实际数据对最优参数进行标定,汇总如表4所示。

Table 4. Social force model parameter value
表4. 社会力模型参数取值
5. 乘客过闸社会力模型仿真
1) 乘客类型
是否携带行李、年龄以及对闸机操作的熟练度是影响乘客过闸效率的重要因素。因此编程时应该对乘客进行分类,编程时将需要输入的乘客分为多类。小件行李乘客:用直径为0.20~0.25 m的空心圆表示;中大件行李乘客:用直径为0.25~0.30 m的空心圆表示。
2) 乘客数量输入
本文仿真所输入的检票人数应该不少于列车的最大定员人数,因此将需要检票旅客数的极值设为1200人 [10]。长沙南站每个检票口有1个人工检票通道和5个检票闸机,每趟列车检票时同时开放南、北两个检票口,每个检票口最多有一趟列车正在检票,因此单侧排队过闸乘客600人。由数据统计可知,自主检票闸机的平均检票速度为10.5人/min,人工检票通道的平均检票速度为23人/min,因此自主检票闸机工作效率与人工检票工作效率之比约为3:2。因此600名乘客中将有360人使用自主检票闸机过闸。

Figure 4. Initial state of passengers before crossing
图4. 过闸前乘客初始状态
再考虑非高峰期与春运时期乘坐高铁出行的乘客类型的差别,即非高峰期时,短距离出行乘客较多,乘客所携带行李数量相对较少,而春运期间,返乡旅客是最多的,大部分乘客都会携带较多行李 [11],因此,在此将小件乘客与大件乘客之比约为1:2。所以在360名乘客中,各类型乘客所占数量如下:无行李乘客120人,中大件行李乘客230人,还有10个老年人。乘客涌入闸机通道的情况如图4所示。
6. 模型检验
按上述参数将乘客排队初始状态输入之后,根据不同的乘客类型编写社会力模型,结合第五节给出的参数数据,对乘客过闸行为进行仿真。由于乘客过闸前均处于等待状态,因此初速度为0,再利用编程时所求出的每个乘客的过闸瞬时速度,按照以下公式求出每个乘客所需过闸时间 [12]。
(13)
(14)
式中:
为
乘客过闸的加速度;
为
乘客过闸时的社会力;
为
乘客的质量;
为
乘客的过闸时间;s为闸机通道长度。
为了检验模型是否科学有效,需要统计出不同类型乘客的过闸平均时间,并与实际统计时间进行比较与调试。利用社会力模型所仿真输出小件行李乘客过闸时间与实际调查的小件行李过闸时间是否存在显著差异,利用SPSS软件的曼–惠特尼U对两组数据进行统计验证与比较,结果如表5、表6所示。

Table 5. Small baggage passengers crossing time sample statistical description
表5. 小件行李乘客过闸时间样本统计描述

Table 6. Analysis of differences in passing time of small baggage passengers
表6. 小件行李乘客时间差异性分析
通过曼–惠特尼U检验在99%精确度下对小件行李过闸时间进行精确分析,发现小件行李乘客实际统计的过闸时间的平均秩(Mean Rank)为289.16,小件行李乘客编程输出的过闸时间的平均秩为324.22,差异较小;秩优先总和分别为135,325、40,203,存在差异;近似概率为0.042 > 0.01。因此接受原假设:认为仿真所输出的携带小件行李过闸时间与实际调查时间不存在显著差异,携带小件行李的乘客过闸平均时间为4.69 s。同理对中大件行李乘客、老年乘客数据进行曼–惠特尼U检验,均不存在显著差异,验证了模型的可靠性。
7. 结论
1) 对乘客过闸行为特性及影响因素进行研究分析发现:男、女乘客过闸时间不存在显著差异,而不同年龄之间存在显著差异;是否携带行李是影响乘客过闸时的重要因素之一,携带小件行李乘客过闸时间与携带中大件行李乘客的过闸时间之间具有显著的差异;影响过闸效率的第三个因素为过闸流程熟练程度。引导老人及携带中大件行李乘客标线从人工通道通行是提高匝机通行效率的措施。
2) 针对影响乘客过闸的三个主要因素:行李、年龄、对过闸流程熟练程度造成延误三个因素,建立了乘客过闸社会力模型。利用matlab编程仿真,以及SPSS数据分析仿真所得过闸时间与现实调研统计过闸时间之间的差异性,检验了乘客过闸社会力模型的科学、有效性。
下一步将对闸机前排队引导线及对乘客过闸机行为综合影响进行研究。