1. 引言
从上世纪50年代起,矿产资源评价经历了从定量化,数字化的发展阶段,目前正在朝深部三维定量预测方向快速地发展。然而,随着预测所涉及的深度不断加深,深部矿产预测已经更加依赖于研究区深部成矿构造推断和矿化分布规律的认识。矿床的形成明显地受地质构造的控制,成矿构造是与矿床形成、改造及保存有关的构造,其不仅表现在空间上对矿床产状的控制,也存在着对矿床形成的约束。因此,针对深部成矿构造及深部成矿作用的研究逐渐成为了当前深部找矿工作中的热点 [1] - [9]。
通过实现对深部区域三维模型的重建可以有助于开展针对深部成矿构造的空间位置、空间形态、空间样式、岩性分布、物质组分和时间序列的研究与分析。因此在深部成矿构造研究中,如何重建深部区域三维模型成为了深部构造研究的热点问题之一。而在三维模型重建过程中时常会伴有不确定性因素的影响,尤其是深部区域,由于数据的相对稀少且地质深部区域复杂,导致探测相对困难。以往的研究工作中结合了大深度物探、深穿透化探和深部钻探等探测技术来探测深部精细结构、深部物性分布和地下物质成分,并运用高分辨率反震法和重力场、地磁场和导电性等深部物性结构特征揭示深部三维精细结构以及深部成矿构造的几何形态和动力机制 [10] [11] [12]。这些研究工作基于地球物理、地球化学探测的深部成矿构造推断已取得一系列成果,但是地球物理反演的多解性和地球化学深穿透推断的不确定性仍然存在,这对深部成矿预测结果的真实性和有效性有着很大的影响。
本文在以往研究模型和数据的基础上,结合了地球物理相关探测数据,将其纳入到贝叶斯模型中进行后续的贝叶斯推断,并根据推断得到的后验概率进行信息熵计算来对研究区域深部成矿构造模型的不确定性进行一定的分析,为后续三维模型的修正提供引导。
2. 研究区地质概况
胶西北金矿集区是世界第三大金矿富集区,发育有三条控矿断裂带,分别为三山岛断裂带,焦家断裂带和招平断裂带,其中,招平断裂带是胶西北区域断裂规模中最大的一条断裂带 [13]。其平面和剖面示意图分别如图1和图2所示。断裂南起平度城北,走向近东西向,至宋格庄逐渐转弯,向北东延伸,经招远城又转为北东东向,经黄城集、蓬莱城以西进入渤海,走向变化南段为5˚~30˚,中断为20˚~45˚,北段变为50˚~70˚,全长120 km,宽度一般50~200 m,断面向南或南东倾斜,倾角30˚~55˚左右。其中,大尹格庄断裂是招平断裂带上的次级断裂,该断裂附近区域富集大量金矿,是整个胶东半岛西北部–胶西北金矿的集中区 [14],其地理位置处于华北克拉通东南缘。
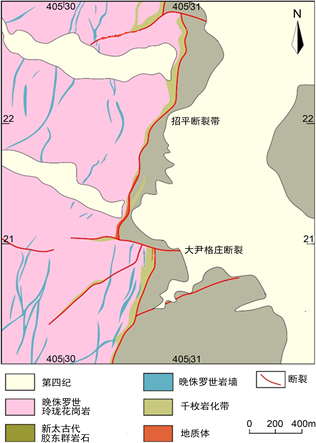
Figure 1. Plan of Zhaoping fault (revisioned from Mao, X. et al., 2019 [15])
图1. 招平断裂带平面示意图(改自Mao, X. et al., 2019 [15])

Figure 2. Section of Zhaoping fault (revisioned from Mao, X. et al., 2019 [15])
图2. 招平断裂带剖面示意图(改自Mao, X. et al., 2019 [15])
该次级断裂长2200 m,宽度一般为2~35米,深度达500 m,水平断距为260至300 m。地表产状表现为波状弯曲、分支复合。走向为100˚,断面向北东方向倾斜,倾角43˚~60˚。横向穿越整个招平断裂带,并导致招平断裂带北部向西方位移。由于该断裂属于后期断裂,黄铁绢英岩角砾、碎块有少量分布。
而在大尹格庄矿区的东部,出露有老地层的变质岩,在断裂的上盘部分,主要分布有黑云変粒岩,斜长角闪岩,浅粒岩,黑云斜长片麻岩夹磁铁石英岩,石榴透辉磁铁石英岩等胶东群。而下盘主要类型则是玲珑岩体。
3. 方法
3.1. 数据介绍
本文结合地物探测数据来对弱地质信息的深部成矿空间进行研究,因此,我们收集到了地物相关的原始数据,通过这些数据可以尽可能的减少整个三维地质模型推断与重建中的不确定性。
3.1.1. 初始三维地质线串模型
我们通过收集研究区域地质剖面图,对其进行矢量化,得到该区域深部成矿构造的线串模型,如图3所示。利用得到的线串模型构造初始的三维模型,以此来为后续的三维模型迭代推断提供基础。

Figure 3. Dayingezhuang fault string model
图3. 大尹格庄断裂线串模型
3.1.2. 重力异常数据
我们收集到了研究区域地面63个采样点的布格重力异常数据,以便为后续贝叶斯推断做准备,这些数据是通过仪器进行重力勘探,再经过一系列布格改正得到的数据。这些数据位于整个大尹格庄矿区范围内,且按一定距离有规则排布,如图4所示。
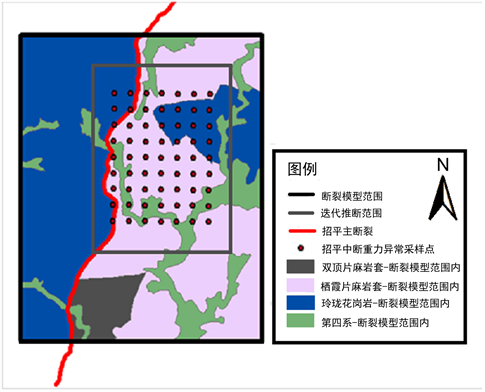
Figure 4. Distribution of sampling points for ground gravity anomalies in Dayingezhuang
图4. 大尹格庄地面重力异常值采样点分布
3.1.3. 岩性密度数据
我们收集到了研究区域上下盘的岩性以及密度参考范围,如表1所示。同时收集到了研究区钻孔数据以及上下盘密度样本,从中选取了上下盘各9个样本,为后续的贝叶斯推断工作做准备。如表2所示。

Table 1. System resulting data of standard experiment (unit: g/cm3)
表1. 上下盘物性参数参考范围(单位:g/cm3)

Table 2. Samples of physical parameters of hanging wall and foot wall (unit: g/cm3)
表2. 上下盘物性参数采样样本(单位:g/cm3)
3.2. 贝叶斯模型
贝叶斯理论发展至今已愈发成熟,这种方法也被越来越多地运用到不确定性表达和推理的研究当中。如Pearl于1986年提出一种简单而有效的贝叶斯网络用来研究不确定性相关问题 [16]。肖张波依据贝叶斯理论实现反演过程中地震数据的有效利用 [17]。李东将贝叶斯理论应用到了对边坡工程模型不确定性分析当中 [18]。本文根据以往研究经验,本文利用贝叶斯原理构造出贝叶斯模型,贝叶斯形式如式(1)所示 [19]:
(1)
其中,
为后验概率,
为似然项,
为先验概率。
本文将贝叶斯模型纳入到三维地质模型不确定性研究中来。利用上述公式,我们在给定了地物观测数据集合
,可以用来对地质界面F进行推断。后验概率
示如式(2)所示:
(2)
其中,
为先验项,
为似然项。我们设定了研究区域深部构造空间为一个由若干个小立体单元构成的大立体空间,给定其中的F为
向量,表示空间中所有立体单元中心点隐函数的集合,
为
向量,表示由地面63个重力异常值测点构成的集合。这里我们舍弃分母,只考虑分子项:
。 (3)
3.2.1. 似然项
我们为上述贝叶斯公式中的似然项
引入物性参数
,以便于更好的求解该项中所表示的概率。因此,似然项可进一步表示为:
(4)
其中,
为
向量,分别表示深部构造空间中上下盘岩石密度。
表示参数
的先验分布,通过利用核密度估计来得到其概率,
则通过计算地面测点的重力异常值来表示。由于该积分的难解性,本文后续利用了MCMC采样方法,将积分离散化为简单求和的形式,在进行均一化处理,最终得到似然函数值。
1) 核密度估计:核密度估计属于一种非参数估计方法,该方法不需要给定数据的先验分布,它是通过数据样本本身出发来估计数据的分布特征 [20]。我们通过收集到上下盘岩性的密度样本,利用核密度估计得到岩性密度的概率分布。
给定物性参数
,参数
的先验分布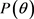 利用核密度估计表示如式(5)所示 [21]:
利用核密度估计表示如式(5)所示 [21]:
(5)
其中,K为核函数,h为带宽。我们这里选取了高斯函数作为核函数,带宽设置为0.25。
2) 重力异常正演:我们选取了位于大尹格庄地表63个观测点的布格重力异常值,假设地面每个观测
点
服从独立同分布,因此
可写成如
的连乘形式。每项
可表示为:
(6)
表示地表观测点的正演计算值。计算公式 [22] 为:
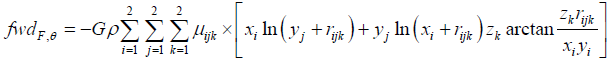 (7)
(7)
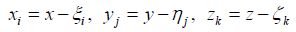 (8)
(8)
(9)
(10)
其中,G为重力常量,
为剩余密度,地表目标观测点坐标为
,每个立体单元的角点坐标为
。重力异常是由于实际地球内部的物质密度分布不均匀产生的,因此我们使用剩余密度作为公式中立体单元的密度来计算重力异常。这里我们考虑使用大尹格庄上下盘密度与地壳密度差值作为剩余密度。采用的大陆地壳地表岩石的密度为2.67 g/cm3。
3.2.2. 先验项
我们利用基于线串模型的隐函数来对深部成矿构造几何边界进行表达。在整个深部成矿构造三维地质空间
中,存在隐函数
使得当且仅当
中的一点
处于无自相交的几何边界上时,满足
,当x处于边界上部时,
;x处于边界下部时,
。将深部成矿构造空间中的上下盘
看作是几何边界的上下部,通过求得每个立方体单元中心点的隐函数值的集合来表示F的先验。其中隐函数是通过计算空间中的点对深部成矿构造的线串模型的距离函数得到的,此处不做过多解释。先验的表示形式如式(11)所示:
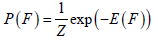 (11)
(11)
其中,Z为分母项,
为每一项先验信息的累加。目前我们考虑了与初始模型一致性的度量作为其先验,如式(12)所示:
(12)
其中,
为初始模型,F为当前迭代得到的模型,其表示包含若干立方体的隐函数的向量,
为与深度相关的系数,深度越深,不确定性越大,
越小,这里考虑倒数作为其系数。
3.3. 贝叶斯推断
构建好贝叶斯模型后,由于其涉及到的高维问题存在一定的难处理性,需要采用一种替代方法来实现对后验分布的近似评估。目前已经开发了多种方法,其中运用最广泛的方法是马尔科夫链蒙特卡洛方法(Markov Chain Monte Carlo),即MCMC方法。该方法本质上使用了马尔科夫的思想,最后得到蒙特卡洛积分,蒙特卡洛积分可以从指定分布中进行抽样,然后通过这些样本构造均值来逼近期望值。其特性在于后一状态只依赖于前一状态,而与以往所经历的状态无关,我们利用这一特性来迭代地绘制参数集的样本 [23]。
MCMC采样方法会根据给定的一个初始值或者一个初始向量,可以采样出下一符合要求的样本,且当前样本只与前一次样本有关。通过每次采出的样本,设置接受率,再根据给定的接受率来判断当前样本是否被接受,如果是,则作为下一次采样的起始样本。MCMC接受率 [24] 表示如式(13)所示:
(13)
其中,z表示前一个样本, z* 表示当前样本,
为后验概率, 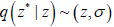 。
。
本文利用MCMC方法与贝叶斯模型结合起来进行贝叶斯推断。我们对涉及到的参数密度进行MCMC采样,并得到所需样本,这样可以将贝叶斯推断中的似然函数的积分问题转化为简单的离散求和形式处理,最后进行均一化处理,如式(14)所示:
(14)
之后,我们针对研究区域深部成矿构造线串模型进行扰动,即对线串上的每个点设定一个扰动阈值,新的线串上的点是在这个阈值中生成的。最终得到新的线串模型。由于扰动过程中,每个数据点存在不相关性,因此扰动线串呈现锯齿状。对此,我们为新扰动的线串数据点设置一定的约束条件,使其扰动合理。我们用一开始的数据点构建图,使其扰动后的数据点按照设定的图结构来约束,从而达到平滑线串的目的。得到新线串之后,再针对每一个线串计算整个成矿构造空间中对应的隐函数集合,通过这些得到的隐函数作为先验条件得出其所对应的后验概率,再同样利用MCMC方法对后验概率进行采样,最终得到符合要求的线串模型样本为后续不确定性的可视化提供基础。
3.4. 信息熵
本文使用信息熵的表示方法来对三维地质模型的不确定性进行度量,这种方法被广泛应用于结构地质背景下的不确定性研究中。信息熵公式 [25] 如下:
(15)
其中,
表示随机事件
的概率。如果事件发生的概率越大,不确定性就越小,信息熵也越小。反之,则越大。
前文中提到,我们通过MCMC方法对扰动的线串进行采样,得到了n种不同的线串数据集,最终产生n种不同的模型展示。我们设定x为深部成矿构造空间中的每一个立方体单元,F为地层地质单元,表示不同的岩性类型,本文中只考虑两种地层单元,即上下盘。则整个构造空间中每一个立体单元x的指示函数
为:
 (16)
(16)
对于n个线串模型,我们使用以下函数来估算每个立体单元的信息概率:
(17)
将得到的每个立体单元的信息概率
带入到式(15)中,可以求得其信息熵值,最终将整个深部成矿构造空间中的所有立体单元的信息熵展示出来,从而实现对不确定性的可视化。
4. 结果
4.1. 物性参数分布
我们通过表2的上下盘岩性密度数据其作为用于概率估计的数据样本,利用核密度估计方法对采样数据进行概率估计。最终得到上下盘的概率密度分布,如图5所示。
 (a)
(a) 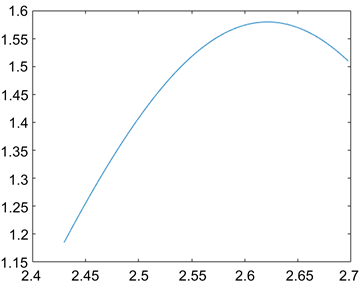 (b)
(b)
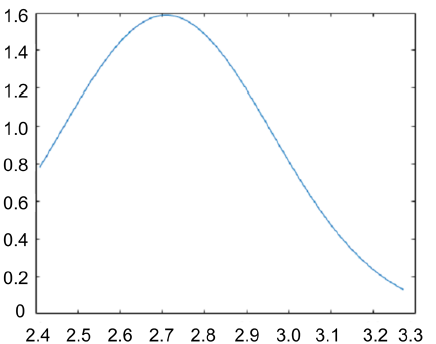
Figure 5. (a) Physical Property Probability Density Distribution of hanging wall; (b) Physical Property Probability Density Distribution of foot wall
图5. (a) 上盘物性参数概率密度分布;(b) 下盘物性参数概率密度分布
图5表明,上盘的物性参数采样样本主要集中于2.74 g/cm3左右,下盘主要集中在2.62 g/cm3左右,且概率密度呈现一定的高斯分布。
4.2. 不确定性可视化
4.2.1
. 物性参数样本
前文中提到,在求解似然函数时遇到了积分问题,积分求解相对困难,因此,本文在贝叶斯推断过程中,利用了MCMC方法对参数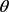 进行了采样。在采样过程中,我们根据收集到的研究区域上下盘物性参数的参考范围,为采样程序设定上下阈,并为上下盘分别输入一个采样所需的初始物性密度值。利用图5中得到的上下盘概率密度函数,最终采样得了上下盘各1000个密度样本。样本的频数分布如图6所示。
进行了采样。在采样过程中,我们根据收集到的研究区域上下盘物性参数的参考范围,为采样程序设定上下阈,并为上下盘分别输入一个采样所需的初始物性密度值。利用图5中得到的上下盘概率密度函数,最终采样得了上下盘各1000个密度样本。样本的频数分布如图6所示。
 (a)
(a)  (b)
(b)
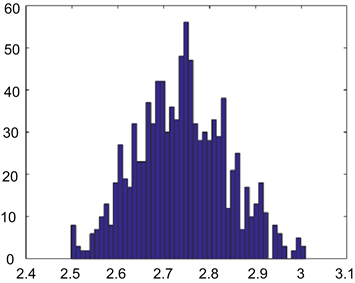
Figure 6. (a) Physical parameters Samples of hanging wall; (b) physical parameters Samples of foot wall
图6. (a) 上盘物性参数采样样本;(b) 下盘物性参数采样样本
图6表明,利用MCMC方法采样得到的结果与图5概率密度分布趋势吻合,呈现一定的高斯分布,且采样结果处于合适的密度范围,可以用于后续的贝叶斯推断。
4.2.2
. 信息熵
我们根据收集到的研究区域初始线串模型扰动出了100个线串并计算得到每个线串的隐函数模型,再利用前文中物性参数采样结果进行贝叶斯推断,得到每个线串的后验概率,基于这些后验概率设置新的接受率,从中接受了其中的71个样本,最终计算得到了信息熵的模型,结果如图7所示。

Figure 7. Three-dimensional model information entropy of deep metallogenic structure
图7. 深部成矿构造三位模型信息熵
信息熵越大,则不确定性越大,图7中所示红色区域表示的信息熵最大,代表该区域不确定性最大,而这部分区域很多集中在模型中部陡峭位置,这是由于该区域地势复杂,在对三维模型进行构造的过程中难免会有比较大的误差,存在较大的不确定性;而随着预测深度的加深,模型也呈现出部分信息熵较大区域,这是由于深部区域数据稀少,不确定性随着深度的增加而增加,通过这种方法可以很直观的展示出三维地质模型的不确定性。
5. 结论
1) 本文根据大尹格庄矿床钻孔的物性参数采样样本,利用核密度估计方法得到了位于该研究区域断裂的上下盘密度概率分布,为地质三维模型不确定性研究提供非常重要的基础。
2) 本文根据大尹格庄矿床重力异常数据,建立贝叶斯框架中的似然函数,并结合MCMC方法推断了招平断裂面形态的后验概率分布,基于此后验概率,采用信息熵方法对三维地质模型的不确定性进行了可视化。通过结果可发现出地下地质特征的复杂性和数据的有限性是造成模型不确定性的主要原因。通过计算得到的可视化模型是建立在当前输入的三维地质模型基础上,这可以很直观的展现该模型的不确定性,有助于引导三维地质模型修正工作沿着不确定性更小的部位开展深部三维结构重建。