损失规避行为下的一般保险公司最优投资再保险问题

Optimal Investment and Reinsurance Problem for a General Insurance Company under Behavior of Loss Aversion

摘要: 本文研究的是基于损失规避的一般保险公司(包括保险公司和再保险公司)的最优投资再保险问题。管理者管理风险通过购买比例再保险和投资金融市场。假设索赔过程服从一个带漂移项的布朗运动，保费率采用期望值原则。保险公司和再保险公司在金融市场中都被允许投资无风险资产和风险资产。风险资产的价格过程服从跳扩散过程。目标是最大化保险公司和再保险公司的共同利益，即最大化财富过程权重和的S-型期望效应。应用鞅方法，我们推导出最优财富过程权重和及相应的最优策略。最后，我们通过数值例子说明模型的参数对最优策略的影响。

Abstract: In the paper, we study the optimal investment reinsurance problem for general insurance companies (insurance company and reinsurance company) based on behavior of loss aversion. Managers manage risk by purchasing proportional reinsurance and investing in financial markets. Assume that the claim process is described by a Brownian motion with drift. The premium rate is calculated through the expectation principle. Both insurance company and reinsurance company are allowed to invest in risk-free assets and risky assets. The price process of risk assets is subject to a jump-diffusion process. Our goal is to maximize the common interests of insurance company and reinsurance company, i.e. Maximizing the weight sum of the wealth process. Using the martingale method, we derive the closed expression of the optimal wealth process weight and its corresponding optimal investment reinsurance strategies. Finally, numerical examples are provided to show the impact of model parameters on the optimal strategies.

1. 引言

近几年来，保险风险管理问题已经引起大家的广泛关注。投资和再保险成为保险公司管理经营公司的重要工具。众所周知，适当的再保险和合理的投资不仅可以对冲其来自索赔的风险而且还可以增加其收益。但是怎样比例的再保险和多大的投资才能增加保险公司抵抗风险的能力，从而提高其收益呢？因此如何选择最优的资产分配策略去保证公司的良性运营成为保险公司急于解决的问题。在早期的投资再保险文献中，大多数学者研究问题主要有三类，一是最大化保险公司终端财富的效应函数的期望(如 Zhang和Chen [1]，Yang和Zhang [2])；二是最小化破产概率(如Browne [3]，Bai and Guo [4]，Zhang et al. [5])；三是时间一致的投资再保险的问题(如Shen and Zeng [6]，Wu and Zeng [7]，Zhang and Liang [8])。在这些准则下，决策者所作的决定都是完全理性的。

但是，由于市场的异样和长期的实证结果动摇了传统的理论对理性决策者的假设基础。因为在复杂的市场中，决策者往往会因为市场环境和自身的心理而表现出不理性的行为。为了弥补这样缺点，人们提出了许多新的理论。其中最著名的理论就是Tversky和Kahneman [9] 提出的累计前景理论。它更加注重决策者的心理多样性。在Tversky和Kahneman [9] 实验和统计中提出了S-型效应函数并被用于最优问题中。例如Berkelaar [10] 研究了损失规避下的最优投资组合。Dong和Zheng [11] 研究了DC养老金在卖空约束下带有S-型效应函数的投资再保险问题。郭 [12] 研究了基于损失规避行为的最优保险投资有和再保险策略的选择。与先前最优投资再保险问题不同的是，我们不单单只考虑了保险公司的利益同时也未忽略到再保险公司的利益。基于累计前景的思想，假定保险公司的经营者是非理性的，决策者可以根据自己的决策参考点来进行再保险和投资。在本文中，我们研究保险公司和再保险公司共同利益的最优投资再保险问题。目标是为了最大化保险公司和再保险公司终端财富的权重和的效应期望。基于损失规避行为(即当保险者的财富过程高于或低于参考点时，其往往会表现出不同的风险偏好和敏感性)，我们采用S-型效用函数。应用鞅方法，我们将动态的最优投资再保险问题转化成静态优化问题，进而推导出保险公司和再保险公司终端财富权重和的最优表达和相应的最优策略。

本文其余的安排如下，在第2节，我们提出基本模型和保险公司和再保险公司财富的权重和。第3节我们介绍S-型效用函数，提出了动态优化问题(6)。第4节构造指数鞅，我们采用鞅方法将动态最优问题转化成静态最优问题，进而推导出保险公司和再保险公司终端财富的权重和的最优表达和相应的最优策略。第5节，参数敏感性的分析。

2. 模型建立

设 $\left(\Omega ,F,P\right)$ 是完备的概率空间， ${\left\{F_t\right\}}_{0\le t\le T}$ 是由， $W_1\left(t\right)$， $W_2\left(t\right)$， $B_1\left(t\right)$ 和 $B_2\left(t\right)$ 五个独立的、标准的一维布朗运动所生成的过滤，表示当前时刻t获得的所有信息, 且假设所有在t时刻作的决定都是基于这些信息。此外，在本文中假设所有的随机变量和随机过程都可以被很好的定义且都是关于 ${\left\{F_t\right\}}_{0\le t\le T}$ 是适应的。

2.1. 盈余过程

如果不考虑再保险，保险公司的盈余过程由经典的C-L风险模型给出

$\text{d}R\left(t\right)=c\text{d}t+{\displaystyle \underset{i=1}{\overset{K\left(t\right)}{\sum }}{Y}_i}$，

其中 $c\ge 0$ 是保费率， ${\displaystyle \underset{i=1}{\overset{N\left(t\right)}{\sum }}{Y}_i}$ 是复合泊松过程，是强度为 ${\lambda }_N$ 的齐次泊松过程， $\left\{Y_i,i\ge 1\right\}$ 是一列正的独立同分布的随机变量，且分布函数为 $F\left(y\right)$。此外，假设 $\left\{K\left(t\right),t\ge 0\right\}$ 和 $\left\{Y_i,i\ge 1\right\}$ 是独立的。记 $\left\{Y_i,i\ge 1\right\}$ 的一阶矩和二阶矩分别为 $E\left[Y_i\right]={\mu }_Y$ 和 $E\left[Y_i^2\right]={\sigma }_Y^2$。我们采用期望值原则去计算保费率，因此，保费率 $c=\left(1+\eta \right){\lambda }_K{\mu }_Y$，其中 $\eta$ 是保险公司的安全荷载。

保险公司也可以通过购买比例再保险或开展新的业务来对冲其风险，从而增强其承担风险的能力。记 ${\pi }_q\left(t\right)\left(0\le {\pi }_q\left(t\right)\le 1\right)$ 是 $t\in \left[0,T\right]$ 时刻比例再保险的水平。假设再保险公司的保费率也采用期望值原则，即再保险公司的保费率为 $\left(1+\theta \right){\lambda }_K{\mu }_Y{\pi }_q\left(t\right)$，其中 $\theta >\eta$ 是再保险公司的安全荷载。注意到，当 $0\le {\pi }_q\left(t\right)\le 1$ 时，相应的保险公司会有一个比例再保险的覆盖。也意味着保险公司会转移一部分风险给再保险公司。在这种情况下，保险公司所承受的索赔额为 $\left(1-{\pi }_q\left(t\right)\right)Y$，再保险公司所承受的索赔额为 ${\pi }_q\left(t\right)Y$ ；当 ${\pi }_q\left(t\right)>1$ 时，保险公司会有来自其他公司额外的业务。

记保险公司总的索赔过程 $H\left(t\right):={\displaystyle \underset{i=1}{\overset{K\left(t\right)}{\sum }}{Y}_i}$ 根据Oksendal和Sulem [13] 给出的结果，一个Levy过程可以被分解成三个部分，即线性部分，布朗运动和纯跳部分。因此，我们可以假设总的累计索赔 $H\left(t\right)$ 满足

$\text{d}H\left(t\right)=A\text{d}t+B\text{d}{W}_0\left(t\right)+\gamma \text{d}N\left(t\right),$

其中 $W_0\left(t\right)$ 和 $N\left(t\right)$ 分别是一维标准的布朗运动和强度为 ${\lambda }_N$ 的过程，A，B和 $\gamma$ 都是常数，满足

$A+{\lambda }_N\gamma ={\lambda }_K{\mu }_Y$, $B^2+{\lambda }_N{\gamma }^2={\lambda }_K{\sigma }_Y^2$.

故考虑再保险之后保险公司的盈余过程 $R_1$ 和再保险公司的盈余过程分布服从下面两个随机微分方程

$\begin{array}{c}\text{d}{R}_1\left(t\right)=\left\{\left[\left(1-{\pi }_q\left(t\right)\right)+\left(\eta -\theta {\pi }_q\left(t\right)\right)\right]{\lambda }_K{\mu }_Y-\left(1-{\pi }_q\left(t\right)\right)A-{\lambda }_N\gamma \left(1-{\pi }_q\left(t\right)\right)\right\}\text{d}t\\ -\left(1-{\pi }_q\left(t\right)\right)B\text{d}{W}_0\left(t\right)-\left(1-{\pi }_q\left(t\right)\right)B\text{d}\tilde{N}\left(t\right),\end{array}$

和

$\text{d}{R}_2\left(t\right)=\left\{\left(1+\theta \right){\lambda }_K{\mu }_Y{\pi }_q\left(t\right)-{\pi }_q\left(t\right)A-{\lambda }_N\gamma {\pi }_q\left(t\right)\right\}\text{d}t-{\pi }_q\left(t\right)B\text{d}{W}_0\left(t\right)-{\pi }_q\left(t\right)\gamma \text{d}\tilde{N}\left(t\right).$

其中 $\tilde{N}\left(t\right)=N\left(t\right)-{\lambda }_{N}t$ 被称为补偿泊松过程，是个鞅。

2.2. 金融市场

除了再保险之外，管理者管理其风险还通过对金融市场的投资。假设保险公司和再保险公司都被允许投资无风险资产和风险资产。其中无风险资产的价格过程满足下面的微分方程

$\frac{\text{d}{S}_0\left(t\right)}{S_0\left(t\right)}=r\text{d}t,S_0\left(0\right)=0,$

保险公司投资的风险资产 $S_1\left(t\right)$ 和再保险公司投资的风险资产 $S_{\text{2}}\left(t\right)$ 的价格过程分别由下面的微分方程给出

$\frac{\text{d}{S}_1\left(t\right)}{S_1\left(t\right)}=a_1\left(t\right)\text{d}t+b_1\left(t\right)\text{d}{W}_1\left(t\right)+{\displaystyle \underset{i=1}{\overset{K_1\left(t\right)}{\sum }}{Y}_i^1},$

和

$\frac{\text{d}{S}_{\text{2}}\left(t\right)}{S_{\text{2}}\left(t\right)}=a_{\text{2}}\left(t\right)\text{d}t+b_{\text{2}}\left(t\right)\text{d}{W}_{\text{2}}\left(t\right)+{\displaystyle \underset{i=1}{\overset{K_{\text{2}}\left(t\right)}{\sum }}{Y}_i^{\text{2}}},$

其中r是常数的无风险利率， $a_j\left(t\right)$ 是第j个风险资产的瞬时收益率， $b_j\left(t\right)$ 是第j个风险资产的波动率。 $a_j\left(t\right)$ 和 $b_j\left(t\right)$ 都是正的有界函数。记 $Y_i^j$ 的一阶矩和二阶矩分别为 $E\left[Y_i^j\right]={\mu }_j$ 和， $E\left[{\left(Y_i^j\right)}^2\right]={\sigma }_j^2$， $K_j\left(t\right)$ 是强度为 ${\lambda }_j$ 的泊松过程，。为了方便假设 $a_j\left(t\right)>r>0$。

对于风险资产中跳过程，我们用扩散过程来逼近，即

$\text{d}{\displaystyle \underset{i=1}{\overset{K_j\left(t\right)}{\sum }}{Y}_i^j}={\lambda }_j{\mu }_j\text{d}t-\sqrt{{\lambda }_j}{\sigma }_j\text{d}{B}_j\left(t\right),j=1,2.$

因此保险公司投资的风险资产 $S_1\left(t\right)$ 和再保险公司投资的风险资产 $S_{\text{2}}\left(t\right)$ 的价格过程可以被重新写为

$\frac{\text{d}{S}_1\left(t\right)}{S_1\left(t\right)}=\left[a_1\left(t\right)+{\lambda }_1{\mu }_1\right]\text{d}t+b_1\left(t\right)\text{d}{W}_1\left(t\right)-\sqrt{{\lambda }_1}{\sigma }_1\text{d}{B}_1\left(t\right),$

和

记 $X_1^{\pi }\left(t\right)$ 和 $X_{\text{2}}^{\pi }\left(t\right)$ 分别是保险公司和再保险公司的总财富过程。设 ${\pi }_{\text{1}}\left(t\right)$ 是保险公司投资在风险资产 $S_1\left(t\right)$ 的总金额， ${\pi }_{\text{2}}\left(t\right)$ 是再保险公司投资在风险资产 $S_{\text{2}}\left(t\right)$ 的总金额，因此 $X_{\text{1}}^{\pi }-{\pi }_1\left(t\right)$ 和 $X_{\text{2}}^{\pi }-{\pi }_{\text{2}}\left(t\right)$ 分别是保险公司和再保险公司分别投资在无风险资产 $S_{\text{0}}\left(t\right)$ 的金额。假设一个贸易策略可以由一个三元组 $\pi \left(t\right):=\left({\pi }_q\left(t\right),{\pi }_1\left(t\right),{\pi }_2\left(t\right)\right)$ 表示。在策略 $\pi \left(t\right)$ 下，保险公司的财富过程 $X_1^{\pi }\left(t\right)$ 和再保险公司的财富过程 $X_{\text{2}}^{\pi }\left(t\right)$ 的价格动态过程分别服从

$\begin{array}{l}\text{d}{X}_1^{\pi }\left(t\right)=\{r{X}_1^{\pi }\left(t\right)+{\pi }_1\left(t\right)\left(a_1\left(t\right)+{\lambda }_1{\mu }_1-r\right)+\left[\left(1-{\pi }_q\left(t\right)\right)+\left(\eta -\theta {\pi }_q\left(t\right)\right)\right]{\lambda }_K{\mu }_Y\\ -\left(1-{\pi }_q\left(t\right)\right)A-{\lambda }_N\gamma \left(1-{\pi }_q\left(t\right)\right)\}\text{d}t-\left(1-{\pi }_q\left(t\right)\right)B\text{d}{W}_0\left(t\right)\\ +{\pi }_1\left(t\right)b_1\left(t\right)\text{d}{W}_0\left(t\right)-{\pi }_1\left(t\right)\sqrt{{\lambda }_1}{\sigma }_1\text{d}{B}_1\left(t\right)-\left(1-{\pi }_q\left(t\right)\right)\gamma \text{d}\tilde{N}\left(t\right)\end{array}$ (1)

和

$\begin{array}{c}\text{d}{X}_2^{\pi }\left(t\right)=\left\{r{X}_2^{\pi }\left(t\right)+{\pi }_2\left(t\right)\left(a_2\left(t\right)+{\lambda }_2{\mu }_2-r\right)+\left(1+\theta \right){\lambda }_K{\mu }_Y{\pi }_q\left(t\right)-{\pi }_q\left(t\right)A-{\lambda }_N\gamma {\pi }_q\left(t\right)\right\}\text{d}t\\ -{\pi }_q\left(t\right)B\text{d}{W}_0\left(t\right)+{\pi }_2\left(t\right)b_2\left(t\right)\text{d}{W}_2\left(t\right)-{\pi }_2\left(t\right)\sqrt{{\lambda }_2}{\sigma }_2\text{d}{B}_2\left(t\right)-{\pi }_q\left(t\right)\gamma \text{d}\tilde{N}\left(t\right),\end{array}$ (2)

其中 $X_1^{\pi }\left(t\right)=x_1,X_{\text{2}}^{\pi }\left(t\right)=x_{\text{2}}$。

为了研究保险公司和再保险公司的共同利益，我们考虑保险公司和再保险公司终端财富的权重和

$Y^{\pi }\left(t\right)={\alpha }_1{X}_1^{\pi }\left(t\right)+{\alpha }_2{X}_2^{\pi }\left(t\right)$ (3)

其中 ${\alpha }_{\text{1}}$ 和 ${\alpha }_2$ 是权重系数，且 ${\alpha }_1,{\alpha }_2\in \left[0,1\right]$。假设 ${\alpha }_1=1-{\alpha }_2$，易知 ${\alpha }_{\text{1}}$ 在保险公司和再保险公司之间做决策的时候会起一个平衡收益的作用。即当 ${\alpha }_{\text{1}}$ 增大时，保险公司财富的权重增加，再保险公司财富的权重减少；反之，当 ${\alpha }_{\text{1}}$ 减少时，保险公司的财富权重减少，再保险公司财富的权重增加。当 ${\alpha }_{\text{1}}=\text{1}$ 时， $Y^{\pi }\left(t\right)$ 就简化成保险公司的财富过程。也可以说它拓展了当前仅考虑保险公司利益的相关文献。通常情况下，在 ${\alpha }_{\text{1}}={\alpha }_{\text{2}}=\frac{\text{1}}{\text{2}}$ 时，财富过程权重和 $Y^{\pi }\left(t\right)$ 等于保险公司财富一半加上再保险公司财富的一半。

根据(1)，(2)和(3)，财富过程权重和 $Y^{\pi }\left(t\right)$ 服从下面随机微分方程

$\begin{array}{l}\text{d}{Y}^{\pi }\left(t\right)=\{r{Y}^{\pi }\left(t\right)+{\alpha }_1\left(1+\eta \right){\lambda }_K{\mu }_Y-{\alpha }_1\left(A+{\lambda }_N\gamma \right)-\left({\alpha }_1-{\alpha }_2\right){\lambda }_K{\mu }_Y{\pi }_q\left(t\right)\\ +{\displaystyle \underset{j=1}{\overset{2}{\sum }}{\alpha }_j}{\pi }_j\left(t\right)\left({\alpha }_j\left(t\right)+{\lambda }_j{\mu }_j-r\right)-\left({\alpha }_1-{\alpha }_2\right)\theta {\lambda }_K{\mu }_Y{\pi }_q\left(t\right)+\left({\alpha }_1-{\alpha }_2\right){\pi }_q\left(t\right)A\\ +\left({\alpha }_1-{\alpha }_2\right){\lambda }_N\gamma {\pi }_q\left(t\right)\}\text{d}t-\left[{\alpha }_1-\left({\alpha }_1-{\alpha }_2\right){\pi }_q\left(t\right)\right]B\text{d}{W}_0\left(t\right)+{\displaystyle \underset{j=1}{\overset{2}{\sum }}{\alpha }_j}{\pi }_j\left(t\right)b_j\left(t\right)\text{d}{W}_j\left(t\right)\\ -{\displaystyle \underset{j=1}{\overset{2}{\sum }}{\alpha }_j{\pi }_j}\left(t\right)\sqrt{{\lambda }_j}{\sigma }_j\text{d}{B}_j\left(t\right)-\left[{\alpha }_1-\left({\alpha }_1-{\alpha }_2\right){\pi }_q\left(t\right)\right]\gamma \text{d}\tilde{N}\left(t\right),\end{array}$ (4)

其中 $Y^{\pi }\left(0\right)=y:={\alpha }_1{x}_1+{\alpha }_2{x}_2$。

定义1：

对于任意 $t\in \left[0,T\right]$，交易策略 $\pi \left(t\right):=\left({\pi }_q\left(t\right),{\pi }_1\left(t\right),{\pi }_2\left(t\right)\right)$ 是可行策略，需要满足下列条件。对于初始状态 $\left(t,s_1,s_2\right)\in \left[\text{0},T\times R\times R\right]$，

(1) $\pi \left(t\right):=\left({\pi }_q\left(t\right),{\pi }_1\left(t\right),{\pi }_2\left(t\right)\right)$ 是可测的。

(2) 对于任意 $t\in \left[0,T\right]$， ${\pi }_q\in \left[0,1\right]$， ${\pi }^{\text{2}}\left(t\right)={\pi }_q^2\left(t\right)+{\pi }_1^2\left(t\right)+{\pi }_2^2\left(t\right)$。

(3) 方程(4)有唯一解。

对于 $\forall \left(t,s_1,s_2\right)\in \left[0,T\right]\times R\times R$，随机微分方程(4)有唯一的解 $Y^{\pi }\left(t\right),t\in \left[0,T\right]$ 且 $E_{t,y}\left[U\left(Y^{\pi }\left(t\right)\right)\right]<\infty$。记是所有可行策略的集合。

3. S-型效用函数的优化问题

在早期投资再保险问题中，大多数文献中所采用效用函数是指数效用函数。在这种情况下，管理者所做的决策都是较理性的。但是由于市场的异样及管理者自身的心理影响，管理者所做的决定往往是非理性的。根据Kahnneman和和Tversky [9] 研究大多数的投资者都是损失厌恶的，他们所做的决定都是根据自己决策的参考点来进行决策的。因此Kahnneman和和Tversky [9] 提出了一个S-型效用函数来表征人们相对于参考点的收益和损失的不同行为(即对损失的敏感性比收益的敏感性更大)。在数值上，S-型效用函数在 $\left[0,\infty \right]$ 有如下定义

$U\left(x\right)=\{\begin{array}{l}{U}_1\left(x\right),x>0,\\ U_2\left(x\right),x<0.\end{array}$

其中 $U_1(\cdot ):R^{+}\to R^{+},{U^{\prime }}_1(\cdot )>0,{U^{″}}_1(\cdot )<0$ ； $U_{\text{2}}(\cdot ):R^{-}\to R^{-},{U^{\prime }}_{\text{2}}(\cdot )<0,{U^{″}}_{\text{2}}(\cdot )>0$。 $U_1(\cdot ),U_2(\cdot )$ 满足下面条件： $U_1\left(0\right)=0,{U^{\prime }}_1\left(0+\right)=+\infty ,{U^{\prime }}_1\left(+\infty \right)=0,U_2\left(0\right)=0,{U^{\prime }}_2\left(0-\right)=+\infty ,{U^{\prime }}_2\left(-\infty \right)=0$。 $U_{\text{2}}(\cdot )$ 的图像比 $U_1(\cdot )$ 更陡，说明决策者对损失的敏感性比收益的敏感性更强。

在本文中，我们采用Kahnneman和和Tversky [9] 给出的一种特殊情况S-型效应函数，如下

$U\left(x\right)=\{\begin{array}{l}A{x}^{{\gamma }_1},x>\xi ,\\ -B{\left(-x\right)}^{{\gamma }_2},x\le \xi ,\end{array}$ (5)

其中 $0<{\gamma }_1\le \gamma {}_2\le 1,0<A<B$，B是损失规避系数。 $\xi$ 是损失与收益的参考点且 $\xi$ 的选择与初始财富有关。更多关于S-型效应函数的文献有Kahnneman和和Tversky [9]，Dong和Zhang [11]。(5)也可以下成下面的形式

$U\left(X\left(t\right)\right)=U_1\left(X\left(t\right)-\xi \right)I_{x>\xi }+U_2\left(X\left(t\right)-\xi \right)I_{x\le \xi },$

其中 $I(\cdot )$ 为指示函数。

对于 $\forall t\in \left[0,T\right]$，管理者旨在找到最优的财富分配策略去最大化保险公司和再保险公司共同利益。即最大化终端财富权重和的S-型效用期望，

$\underset{\pi \in \Pi }{\max }{E}_{t,y}\left[U\left(Y^{\pi }\left(T\right)\right)\right],$ (6)

其中限制，对 $\forall t\in \left[0,T\right]$ 表示保险公司在整个投资期间内不会破产。

4. 在S-型效用函数下的最优投资再保险策略

在本节中，我们的目的是找到使得保险公司和再保险公司共同利益最大化的最优策略。我们运用鞅方法将动态决策问题(6)转化成一个静态优化问题，然后运用拉格朗日乘子来求解最优问题。首先我们定义随机折扣因子 $G\left(t\right)$ (参考文献 [12])，

$\begin{array}{c}G\left(t\right)=\exp \{-rt-{\displaystyle \underset{j=0}{\overset{2}{\sum }}{\displaystyle {\int }_0^t{\theta }_j\left(s\right)\text{d}{W}_j\left(s\right)}}-\frac{1}{2}{\displaystyle {\int }_0^t{\displaystyle \underset{j=0}{\overset{2}{\sum }}{\theta }_j^2\left(s\right)\text{d}s}}-{\displaystyle \underset{j=1}{\overset{2}{\sum }}{\tilde{\theta }}_j\left(s\right)\text{d}{B}_j\left(s\right)}\\ -\frac{1}{2}{\displaystyle {\int }_0^t{\displaystyle \underset{j=1}{\overset{2}{\sum }}{\tilde{\theta }}_j^2\left(s\right)\text{d}s}}+{\displaystyle {\int }_0^t\ln \left[1+{\theta }_3\left(s\right)\right]\text{d}N\left(s\right)}-{\lambda }_N{\displaystyle {\int }_0^t{\theta }_3\left(s\right)\text{d}s}\}.\end{array}$

其中 ${\theta }_j\left(t\right),j=0,1,2$ 和 ${\tilde{\theta }}_j\left(t\right),j=1,2$ 满足下面的方程组

根据Itô公式， $G\left(t\right)$ 有如下微分形式

$\text{d}G\left(t\right)=G\left(t\right)\left[-r\text{d}t-{\displaystyle \underset{j=0}{\overset{2}{\sum }}{\theta }_j\left(t\right)\text{d}{W}_j\left(t\right)}-{\displaystyle \underset{j=\text{1}}{\overset{2}{\sum }}{\tilde{\theta }}_j\left(t\right)\text{d}{B}_j\left(t\right)}+{\theta }_3\left(t\right)\text{d}\tilde{N}\left(t\right)\right].$

接下来我们引入一个新的随机变量 $Z\left(t\right)$，

$Z\left(t\right)=Y\left(t\right)-g\left(t\right),$ (7)

$g\left(t\right)$ 的经济含义表示保险公司即不考虑投资也不考虑再保险。故在数值上，

$g\left(t\right)={\text{e}}^{{\alpha }_{1}rt}\left[C{\displaystyle {\int }_0^t{\text{e}}^{-{\alpha }_{1}rs}\text{d}s}-B{\displaystyle {\int }_0^t{\text{e}}^{-{\alpha }_{1}rs}\text{d}{W}_0\left(s\right)-{\alpha }_1\gamma {\displaystyle {\int }_0^t{\text{e}}^{-{\alpha }_{1}rs}\text{d}\tilde{N}\left(s\right)}}\right]$ (8)

其中 $C=\mu {\lambda }_K{\mu }_Y$。

根据(4)，(7)和(8)， $Z\left(t\right)$ 的微分形式如下

$\begin{array}{c}\text{d}Z\left(t\right)=\{r{Z}^{\pi }\left(t\right)-\left({\alpha }_1-{\alpha }_2\right){\lambda }_K{\mu }_Y{\pi }_q\left(t\right)-\left({\alpha }_1-{\alpha }_2\right)\theta {\lambda }_K{\mu }_Y{\pi }_q\left(t\right)+\left({\alpha }_1-{\alpha }_2\right){\pi }_q\left(t\right)A\underset{}{\overset{}{}}\\ +{\displaystyle \underset{j=1}{\overset{2}{\sum }}{\alpha }_j{\pi }_j\left(t\right)\left({\alpha }_j\left(t\right)+{\lambda }_j{\mu }_j-r\right)+\left({\alpha }_1-{\alpha }_2\right){\lambda }_N\gamma {\pi }_q\left(t\right)}\}\text{d}t+\left({\alpha }_1-{\alpha }_2\right){\pi }_q\left(t\right)B\text{d}{W}_0\left(t\right)\\ +{\displaystyle \underset{j=1}{\overset{2}{\sum }}{\alpha }_j{\pi }_j\left(t\right)b_j\text{d}{W}_j\left(t\right)-{\displaystyle \underset{j=1}{\overset{2}{\sum }}{\alpha }_j{\pi }_j\left(t\right)\sqrt{{\lambda }_j}{\sigma }_j\left(t\right)\text{d}{B}_j\left(t\right)}}+\left({\alpha }_1-{\alpha }_2\right){\pi }_q\left(t\right)\gamma \text{d}\tilde{N}\left(t\right).\end{array}$

其中 $Z\left(0\right)=y$。

为了最大化保险公司和再保险公司终端财富权重和 $Y^{\pi }\left(t\right)$ 的S-型效应函数期望，我们引入下面两个引理是有必要的。

引理4.1 $\forall t\in \left[0,T\right]$， $G\left(t\right)Z\left(t\right)$ 是P-鞅。

证 由Levy过程的Itô公式可知

$\begin{array}{c}\text{d}G\left(t\right)Z\left(t\right)=G\left(t\right)\left[\left({\alpha }_1-{\alpha }_2\right){\pi }_q\left(t\right)B-Z\left(t\right){\theta }_0\left(t\right)\right]\text{d}{W}_0\left(t\right)\\ +G\left(t\right){\displaystyle \underset{j=1}{\overset{2}{\sum }}\left[{\alpha }_j{\pi }_j\left(t\right)b_j\left(t\right)-{\theta }_j\left(t\right)Z\left(t\right)\right]\text{d}{W}_j\left(t\right)}\\ -G\left(t\right){\displaystyle \underset{j=1}{\overset{2}{\sum }}\left[{\alpha }_j{\pi }_j\left(t\right)\sqrt{{\lambda }_j}{\sigma }_j\left(t\right)+{\tilde{\theta }}_j\left(t\right)Z\left(t\right)\right]\text{d}{B}_j\left(t\right)}\\ +G\left(t\right)\left[Z\left(t\right){\theta }_3\left(t\right)+\left({\alpha }_1-{\alpha }_2\right){\pi }_q\left(t\right)\left(1+{\theta }_3\left(t\right)\right)\gamma \right]\text{d}\tilde{N}\left(t\right),\end{array}$ (9)

显然， $G\left(t\right)Z\left(t\right)$ 可以表示成布朗运动积分的形式。故 $G\left(t\right)Z\left(t\right)$ 是一个P-鞅。由鞅的性质( $G\left(t\right)Z(t)$

是鞅，则 $G\left(t\right)Z\left(t\right)$ 一定是上鞅)，因此有 $E\left[G\left(T\right)Z\left(T\right)\right]\le y$。

引理4.2(见文献Guo [9])设随机变量 $\delta$ 是可测的，那么对于任意给定的初始财富 $y>0$ 满足

$E\left[G\left(t\right)\delta \right]=y$，

则存在策略 $\pi \left(t\right)=\left({\pi }_q\left(t\right),{\pi }_1\left(t\right),{\pi }_2\left(t\right)\right)\in \Pi$ 使得 $Z^{\pi }\left(T\right)=\delta$。

通过引理4.1和引理4.2知，动态最优问题(6)等价与下面的静态优化问题

$\{\begin{array}{l}\underset{\pi \in \Pi }{\max }E\left[U\left(\delta \right)\right]\\ E\left[G\left(T\right)\delta \right]\le y\end{array}$ (10)

与Guo [14] 有相似的结论,最优静态问题(10)的最优解

${\delta }^{*}=\{\begin{array}{l}\xi +\left[y-E\left[G\left(T\right)\xi \right]\right]\frac{G{\left(T\right)}^{\frac{1}{{\gamma }_1-1}}}{E\left[G{\left(T\right)}^{\frac{{\gamma }_1}{{\gamma }_1-1}}\right]},\xi \le Z{\text{e}}^{rT},\\ 0,\xi >Z{\text{e}}^{rT},\end{array}$ (11)

因此我们可以推导出对应的动态优化问题(6)的最优策略 ${\pi }^{\text{*}}$， $Z^{*}\left(T\right)=Z^{{\pi }^{*}}\left(T\right)={\delta }^{*}$。乘以随机折现因子 $G\left(T\right)$ 后，取条件期望有

$E\left[G\left(T\right)Z^{*}\left(T\right)|F_t\right]=E\left[G\left(T\right)\delta |F_t\right].$ (12)

根据引理4.2，(11)和(12)，我们有

$G\left(t\right)Z^{*}\left(t\right)=\{\begin{array}{l}G\left(T\right)\xi +\left[y-E\left[G\left(T\right)\xi \right]\right]\frac{G{\left(T\right)}^{\frac{1}{{\gamma }_1-1}}}{E\left[G{\left(T\right)}^{\frac{{\gamma }_1}{{\gamma }_1-1}}\right]},\xi \le Z{\text{e}}^{rT}\\ 0,\xi >Z{\text{e}}^{rT}\end{array}$ (13)

接下来为了简化(13)，定义指数鞅 $M\left(t\right)$，

$\begin{array}{c}M\left(t\right)=\exp {\{-{\displaystyle \underset{j=0}{\overset{2}{\sum }}\frac{1}{2}\left(\frac{{\gamma }_1}{{\gamma }_1-1}\right)}}^2{\displaystyle {\int }_0^t{\theta }_j^2\left(s\right)\text{d}s-{\displaystyle \underset{j=0}{\overset{2}{\sum }}\left(\frac{{\gamma }_1}{{\gamma }_1-1}\right){\displaystyle {\int }_0^t{\theta }_j\left(s\right)\text{d}{W}_j\left(s\right)}}}\\ -{\displaystyle \underset{j=1}{\overset{2}{\sum }}\frac{1}{2}{\left(\frac{{\gamma }_1}{{\gamma }_1-1}\right)}^2{\displaystyle {\int }_0^t{\tilde{\theta }}_j^2\left(s\right)\text{d}s}}-{\displaystyle \underset{j=1}{\overset{2}{\sum }}\frac{{\gamma }_1}{{\gamma }_1-1}{\displaystyle {\int }_0^t{\tilde{\theta }}_j\left(s\right)\text{d}{B}_j\left(s\right)}}\\ -{\displaystyle {\int }_0^t\left({\left(1+{\theta }_3\left(s\right)\right)}^{\frac{{\gamma }_1}{{\gamma }_1-1}}\right){\lambda }_N\text{d}s}+\frac{{\gamma }_1}{{\gamma }_1-1}{\displaystyle {\int }_0^t\ln \left(1+{\theta }_3\left(s\right)\right)\text{d}N\left(s\right)}.\end{array}$

因此

$\begin{array}{c}G{\left(t\right)}^{\frac{{\gamma }_1}{{\gamma }_1-1}}=M\left(t\right)f\left(t\right)\\ =M\left(t\right)[\exp \{-\frac{{\gamma }_1}{{\gamma }_1-1}rt+{\displaystyle \underset{j=1}{\overset{2}{\sum }}\frac{1}{2}\frac{{\gamma }_1}{{\left({\gamma }_1-1\right)}^2}{\displaystyle {\int }_0^t{\theta }_j^2\left(t\right)\text{d}s}+}{\displaystyle \underset{j=1}{\overset{2}{\sum }}\frac{1}{2}}\frac{{\gamma }_1}{{\left({\gamma }_1-1\right)}^2}\\ \times {\displaystyle {\int }_0^t{\tilde{\theta }}_j^2\left(s\right)\text{d}s}+{\displaystyle {\int }_0^t\left({\left(1+{\theta }_3\left(s\right)\right)}^{\frac{{\gamma }_1}{{\gamma }_1-1}}-{\theta }_3\left(s\right)-1\right){\lambda }_N\text{d}s}\}]\end{array}$

故

$\frac{E\left[G{\left(T\right)}^{\frac{{\gamma }_1}{{\gamma }_1-1}}|F_t\right]}{E\left[G{\left(T\right)}^{\frac{{\gamma }_1}{{\gamma }_1-1}}\right]}=\frac{E\left[M\left(T\right)f\left(T\right)|F_t\right]}{f\left(T\right)E\left[M(T)\right]}=\frac{M\left(t\right)}{M\left(0\right)}=M\left(t\right).$

注意到， $E\left[G\left(t\right)\right]={\text{e}}^{-rt}$，则我们有

$\begin{array}{c}\text{d}G\left(t\right)Z^{*}\left(t\right)=\xi \text{d}G\left(t\right)+\left[y-\xi {\text{e}}^{-rT}\right]\text{d}M\left(t\right)\\ =\xi \left\{G\left(t\right)\left[-r\text{d}t-{\displaystyle \underset{j=0}{\overset{2}{\sum }}{\theta }_j\left(t\right)\text{d}{W}_j\left(t\right)-{\displaystyle \underset{j=1}{\overset{2}{\sum }}{\tilde{\theta }}_j\left(t\right)\text{d}{B}_j\left(t\right)+{\theta }_3\left(t\right)\text{d}\tilde{N}\left(t\right)}}\right]\right\}\\ +\left[y-\xi {\text{e}}^{-rT}\right]M\left(t\right)\left[-{\displaystyle \underset{j=0}{\overset{2}{\sum }}\frac{{\gamma }_1}{{\gamma }_1-1}{\theta }_j\text{d}{W}_j\left(t\right)-{\displaystyle \underset{j=1}{\overset{2}{\sum }}\frac{{\gamma }_1}{{\gamma }_1-1}{\tilde{\theta }}_j\text{d}{B}_j\left(t\right)}}\right]\\ -\left({\left(1+{\theta }_3\left(t\right)\right)}^{\frac{{\gamma }_1}{{\gamma }_1-1}}-1\right)\text{d}\tilde{N}(t)\end{array}$

$\begin{array}{l}=-r\xi G\left(t\right)+G\left(t\right){\displaystyle \underset{j=0}{\overset{2}{\sum }}\left[\frac{{\gamma }_1}{{\gamma }_1-1}{Z}^{{\pi }^{*}}\left(t\right)-\frac{1}{1-{\gamma }_1}\xi \right]{\theta }_j\left(t\right)\text{d}{W}_j\left(t\right)}\\ +G\left(t\right){\displaystyle \underset{j=1}{\overset{2}{\sum }}\left[\frac{{\gamma }_1}{{\gamma }_1-1}{Z}^{{\pi }^{*}}\left(t\right)-\frac{1}{1-{\gamma }_1}\xi \right]{\tilde{\theta }}_j\left(t\right)\text{d}{B}_j\left(t\right)}\\ +G\left(t\right)\left[\left({\left(1+{\theta }_3\left(t\right)\right)}^{\frac{{\gamma }_1}{{\gamma }_1-1}}-1\right)\times \left(Z^{{\pi }^{*}}\left(t\right)-\xi \right)+\xi {\theta }_3\left(t\right)\right]\text{d}\tilde{N}\left(t\right).\end{array}$ (14)

同时 $G\left(t\right)Z^{{\pi }^{*}}\left(t\right)$ 也满足(9)

$\begin{array}{c}\text{d}G\left(t\right)Z^{{\pi }^{*}}\left(t\right)=G\left(t\right)\left[\left({\alpha }_1-{\alpha }_2\right){\pi }_q\left(t\right)B-Z^{{\pi }^{*}}\left(t\right){\theta }_0\left(t\right)\right]\text{d}{W}_0\left(t\right)\\ +G\left(t\right){\displaystyle \underset{j=1}{\overset{2}{\sum }}\left[{\alpha }_j{\pi }_j\left(t\right)b_j\left(t\right)-{\theta }_j\left(t\right)Z^{{\pi }^{*}}\left(t\right)\right]\text{d}{W}_j\left(t\right)}\\ -G\left(t\right){\displaystyle \underset{j=1}{\overset{2}{\sum }}\left[{\alpha }_j{\pi }_j\left(t\right)\sqrt{{\lambda }_j}{\sigma }_j+{\tilde{\theta }}_j\left(t\right)Z^{{\pi }^{*}}\left(t\right)\right]\text{d}{B}_j\left(t\right)}\\ +G\left(t\right)\left[Z^{{\pi }^{*}}\left(t\right){\theta }_3\left(t\right)+\left({\alpha }_1-{\alpha }_2\right){\pi }_q\left(t\right)\left(1+{\theta }_3\left(t\right)\right)\gamma \right]\text{d}\tilde{N}\left(t\right).\end{array}$ (15)

比较(14)和(15)我们有

$\{\begin{array}{l}{\pi }_1^{*}\left(t\right)=\left[\frac{a_j\left(t\right)+{\lambda }_j{\mu }_j-r}{a_j\left(b_j^2\left(t\right)+{\lambda }_j{\sigma }_j^2\right)}+\frac{{\gamma }_1}{1-{\gamma }_1}\frac{b_j\left(t\right)-\sqrt{{\lambda }_j}{\sigma }_j}{a_j\left(b_j^2\left(t\right)+{\lambda }_j{\sigma }_j^2\right)}\right]Z^{{\pi }^{*}}\left(t\right)-\frac{1}{1-{\gamma }_1}\frac{b_j\left(t\right)+\sqrt{{\lambda }_j}{\sigma }_j}{a_j\left(b_j^2\left(t\right)+{\lambda }_j{\sigma }_j^2\right)}\xi ,j=1,\text{2,}\\ {\pi }_q^{*}\left(t\right)=\frac{1}{{\alpha }_2-{\alpha }_1}{\omega }^{*}\left(Z^{{\pi }^{*}}\left(t\right)-\xi \right).\end{array}$

其中满足下面的方程

(16)

与Guo [14] 有类似的讨论，方程(16)的解是存在且唯一的。

定理4.1

在时间 $0\le t\le T$,，基于损失规避行为的保险公司和再保险公司的财富权重和和相应的最优投资再保险策略是

$\begin{array}{l}{Y}^{{\pi }^{*}}\left(t\right)=Z^{{\pi }^{*}}\left(t\right)+g\left(t\right)\\ =\{\begin{array}{l}\xi +g\left(t\right)+\left(y-\xi {\text{e}}^{-rT}\right)\exp \{rt-{\displaystyle \underset{j=0}{\overset{2}{\sum }}\frac{1}{1-{\gamma }_1}{\displaystyle {\int }_0^t{\theta }_j\left(s\right)\text{d}{W}_j\left(s\right)}-{\displaystyle \underset{j=0}{\overset{2}{\sum }}\frac{2{\gamma }_1-1}{2{\left({\gamma }_1-1\right)}^2}{\displaystyle {\int }_0^t{\theta }_j^2\left(s\right)\text{d}s}}}\\ -{\displaystyle \underset{j=1}{\overset{2}{\sum }}{\displaystyle {\int }_0^t{\tilde{\theta }}_j\left(s\right)\text{d}{B}_j\left(s\right)}}-{\displaystyle \underset{j=0}{\overset{2}{\sum }}\frac{2{\gamma }_1-1}{2{\left({\gamma }_1-1\right)}^2}{\displaystyle {\int }_0^t{\tilde{\theta }}_j^2\left(s\right)\text{d}s}-{\displaystyle {\int }_0^t\left[{\left({\theta }_3\left(s\right)+1\right)}^{\frac{{\gamma }_1}{{\gamma }_1-1}}-{\theta }_3\left(s\right)-1\right]{\lambda }_N\text{d}s}}\\ +\frac{1}{{\gamma }_1-1}{\displaystyle {\int }_0^t\ln \left(1+{\theta }_3\left(s\right)\right)\text{d}N\left(s\right),\xi \le y{\text{e}}^{rT},}\\ g\left(t\right),\xi >y{\text{e}}^{rT}.\end{array}\end{array}$

和

$\{\begin{array}{l}{\pi }_1^{*}\left(t\right)=\left[\frac{a_j\left(t\right)+{\lambda }_j{\mu }_j-r}{a_j\left(b_j^2\left(t\right)+{\lambda }_j{\sigma }_j^2\right)}+\frac{{\gamma }_1}{1-{\gamma }_1}\frac{b_j\left(t\right)-\sqrt{{\lambda }_j}{\sigma }_j}{a_j\left(b_j^2\left(t\right)+{\lambda }_j{\sigma }_j^2\right)}\right]Z^{{\pi }^{*}}\left(t\right)-\frac{1}{1-{\gamma }_1}\frac{b_j\left(t\right)+\sqrt{{\lambda }_j}{\sigma }_j}{a_j\left(b_j^2\left(t\right)+{\lambda }_j{\sigma }_j^2\right)}\xi ,\\ {\pi }_q^{*}\left(t\right)=\frac{1}{{\alpha }_2-{\alpha }_1}{\omega }^{*}\left(Z^{{\pi }^{*}}\left(t\right)-\xi \right).\end{array}$

其中 ${\omega }^{\text{*}}$ 满足下面的方程

$\gamma {\lambda }_N{\left(1-\gamma \omega \right)}^{{\gamma }_1-1}+\left(1-{\gamma }_1\right)B^2\omega -\left(1+\eta \right){\lambda }_K{\mu }_Y+A=0.$

5. 数值分析

在这一节中，我们呈现数值例子去解释模型参数对最优策略的影响。为了方便起见，在整个数值分析中，不失一般性，基本参数给出

$\begin{array}{l}r=0.02,\eta =0.25,\theta =0.4,{\lambda }_K=4,{\lambda }_N=1,x_1=0.5,x_2=0.5,\\ a_1=0.2,b_1=0.3,a_2=0.4,b_2=0.5,{\lambda }_1=2,{\mu }_1=0.2,{\lambda }_2=2,\\ {\mu }_2=0.2,{\sigma }_1=0.1,{\sigma }_2=0.2,\gamma =0.001,{\mu }_Y=\frac{1}{40},{\sigma }_Y=\frac{1}{{40}^2}.\end{array}$

图1和图2显示了 ${\alpha }_{\text{1}}$， ${\alpha }_{\text{2}}$ 和 $\xi$ 对最优再保险策略的影响。当 ${\alpha }_1<{\alpha }_2$ 时，如图1，随着参考点 $\xi$ 的增加，最优的再保险策略是减少的。也就是说，当参考点越低的时候，决策者表现的较为激进。就也就是说随着参考点的增加，决策者变的相对保守，再保险对决策者的吸引力也随之减弱。但是当参考点 $\xi$ 给定时，越大，最优再保险策略 ${\pi }_q^{*}\left(t\right)$ 越大。意味着随着保险公司权重的增加，决策者更愿意购买更多的再保险来分担自身的风险。相反，当 ${\alpha }_1>{\alpha }_2$，如图2，最优再保险策略随着参考点 $\xi$ 的增加而增加。此时参考点越高，决策者表现的越激进。同时再保险对决策者更具吸引力。

图3和图4显示了保险公司的最优投资策略 ${\pi }_{\text{1}}^{\text{*}}\left(t\right)$ 随着漂移 $a_1$ 和波动 $b_1$ 上升或下降的趋势。从图3中，我们可以明确的看出无论是大于 ${\alpha }_{\text{1}}$ 还是小于 ${\alpha }_{\text{2}}$，随着 ${\alpha }_{\text{1}}$ 的增加，最优投资策略 ${\pi }_{\text{1}}^{\text{*}}\left(t\right)$ 都是增加的。但是当上升的趋势是明显大于 ${\alpha }_1>{\alpha }_2$ 的。也就是说，如果对保险公司的权重小于再保险公司的权重时，对最优投资策略的影响更大。在图4中，最优投资策略 ${\pi }_{\text{1}}^{\text{*}}\left(t\right)$ 随着波动 $b_1$ 有很明显的下降趋势。当 $b_1$ 在0.25之后变化趋势变得平缓。这个也很符合实际。在金融市场中，如果波动很大，那么相对的风险也会增大，决策者在作决定时，就会减少对金融市场中风险资产的投资。

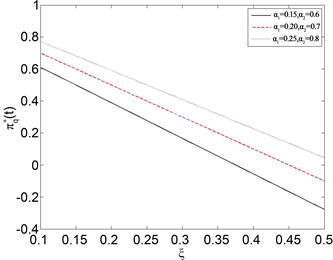
Figure 1. The effect of on the optimal reinsurance strategy ${\pi }_q^{*}\left(t\right)$ when ${\alpha }_1<{\alpha }_2$

图1. ${\alpha }_1<{\alpha }_2$ 时， $\xi$ 对最优再保险策略 ${\pi }_q^{*}\left(t\right)$ 的影响

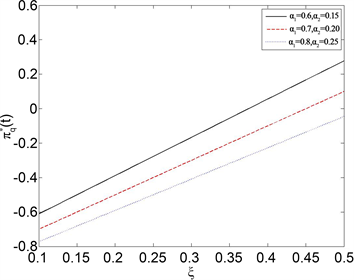
Figure 2. The effect of $\xi$ on the optimal reinsurance strategy ${\pi }_q^{*}\left(t\right)$ when ${\alpha }_1>{\alpha }_2$

图2. ${\alpha }_1>{\alpha }_2$ 时， $\xi$ 对最优再保险策略 ${\pi }_q^{*}\left(t\right)$ 的影响

Figure 3. The effect of $a_1$ on the optimal reinsurance strategy ${\pi }_{\text{1}}^{*}(t)$

图3. $a_1$ 对最优再保险策略 ${\pi }_{\text{1}}^{*}\left(t\right)$ 的影响

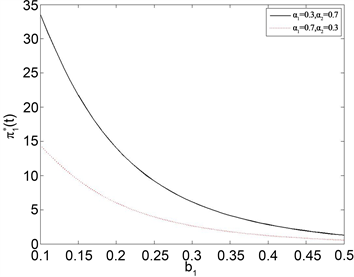
Figure 4. The effect of $b_1$ on the optimal reinsurance strategy ${\pi }_{\text{1}}^{*}(t)$

图4.对最优再保险策略 ${\pi }_{\text{1}}^{*}\left(t\right)$ 的影响

图5和图6显示了再保险公司的投资中模型参数 $a_2$ 和 $b_{\text{2}}$ 对最优投资策略 ${\pi }_{\text{2}}^{\text{*}}\left(t\right)$ 的影响。无论是 ${\alpha }_{\text{1}}$ 大于还是小于 ${\alpha }_{\text{2}}$，最优投资策略 ${\pi }_{\text{2}}^{\text{*}}\left(t\right)$ 随着 $a_2$ 的增加而增加，最优投资策略 ${\pi }_{\text{2}}^{\text{*}}\left(t\right)$ 随着 $b_{\text{2}}$ 的增加而减少的。图5和图6分别与图3和图4有相同的经济解释。这里我们忽略。

Figure 5. The effect of $a_2$ on the optimal reinsurance strategy ${\pi }_{\text{2}}^{*}(t)$

图5. $a_2$ 对最优再保险策略 ${\pi }_{\text{2}}^{*}\left(t\right)$ 的影响

Figure 6. The effect of $b_2$ on the optimal reinsurance strategy ${\pi }_{\text{2}}^{*}(t)$

图6. $b_2$ 对最优再保险策略 ${\pi }_{\text{2}}^{*}\left(t\right)$ 的影响

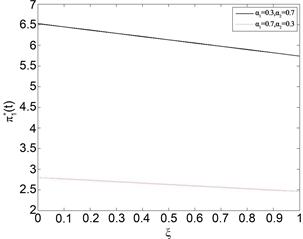
Figure 7. The effect of $\xi$ on the optimal reinsurance strategy ${\pi }_{\text{1}}^{*}(t)$

图7.对最优再保险策略 ${\pi }_{\text{1}}^{*}\left(t\right)$ 的影响

Figure 8. The effect of $\xi$ on the optimal reinsurance strategy ${\pi }_2^{*}(t)$

图8. $\xi$ 对最优再保险策略 ${\pi }_2^{*}\left(t\right)$ 的影响

图7和图8显示了参考点 $\xi$ 对保险公司的最优投资策略 ${\pi }_{\text{1}}^{\text{*}}\left(t\right)$ 和再保险公司的最优投资策略 ${\pi }_{\text{2}}^{\text{*}}\left(t\right)$ 的影响。从图7和图8可以看出无论是大于还是小于 ${\alpha }_{\text{2}}$，投资策略 ${\pi }_{\text{1}}^{\text{*}}\left(t\right)$ 和 ${\pi }_{\text{2}}^{\text{*}}\left(t\right)$ 都是随着参考点 $\xi$ 的增加而减小。也就意味着当参考点降低时，决策者是非理性的。随着参考点 $\xi$ 的增加，保险公司和再保险公司在金融市场的投资比例都在相应的减少，此时决策者会变得更加保守，表现出风险厌恶的特性。

6. 总结

在文章中，我们研究了损失规避下一般保险公司的最优投资再保险问题。金融市场的投资包括无风险投资和风险投资，其中风险投资服从跳扩散过程。采用鞅方法，我们得到了财富过程的权重和以及最优投资再保险策略。此外，我们对最优投资策略和再保险策略进行了敏感性分析。