1. 引言
众所周知,国内生产总值(GDP)是指按市场价格计算的一个国家(或地区)所有常住单位在一定时期内生产活动的最终成果,常被公认为衡量国家经济状况的最佳指标。国内生产总值GDP是核算体系中一个重要的综合性统计指标,也是我国新国民经济核算体系中的核心指标,它反映了一国(或地区)的经济实力和市场规模。
而第一产业是指通过人类劳动直接从自然界取得产品的部门。我国规定专指农、林、牧、渔业。第二产业是指对第一产业和本产业提供的产品(原料)进行加工的部门,我国规定专指采矿业,制造业,电力、燃气及水的生产和供应业,建筑业。第三产业是指对消费者提供最终服务和对生产者(包括三个产业的生产者)提供中间服务的部门。指除第一、二产业以外的其他行业。这三种产业深深影响着GDP的增速,因此弄清楚四者之间的关系,对于我国今后的经济增长起着有力的推动作用。
2. 一元回归模型的建立
2.1. 普通最小二乘估计
2.1.1. 普通最小二乘回归方程求解
根据相关文献 [1] 及生活经验,我们容易得出,第一产业增加值 对GDP y有着较为显著的影响,我们通过大数据平台 [2] 获得了1990~2012年国内GDP、第一产业增加值的数据。
对GDP y有着较为显著的影响,我们通过大数据平台 [2] 获得了1990~2012年国内GDP、第一产业增加值的数据。
由普通最小二乘法
(3-1)
(3-2)
(公式里
对应第一产业
的相应值,
对应GDP的相应值)。
利用SPSS软件 [3],输出结果见表1:

Table 1. The output of ordinary least squares regression to primary sector of the economy and GDP
表1. 普通最小二乘回归对第一产业增加值和GDP的输出结果
a. 因变量:GDP。
其中回归系数显著性检验
,远小于显著性水平
,因此y与
的线性回归高度显著。
由系数一栏的输出结果可以得出,
,
,且二者P值均小于显著性水平
,因此二者均高度显著。所以GDP y与第一产业
所建立的普通最小二乘回归方程为
(3-3)
这表明第一产业
每增加一个单位,相应的GDP平均增加11.083个单位。
2.1.2. 残差分析
由上述建立的一元线性回归方程,利用SPSS软件,计算出每一项所对应的残差
的值。
以残差为纵坐标,第一产业增加值为横坐标,利用R软件,画出图像见图1:
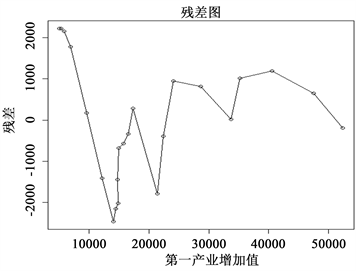
Figure 1. Residuals for different primary sector of the economy
图1. 不同第一产业增加值的残差图
由以上残差图可以看出,残差之均匀的散落在直线
两侧,但存在一定的异方差性,说明以上的普通最小二乘法存在一定的局限性。
2.2. 一元加权最小二乘估计
2.2.1. 异方差性的检验
利用等级相关系数,通过SPSS软件,所得输出结果见表2:

Table 2. Rank correlation coefficient output
表2. 等级相关系数输出结果
**.在0.01级别(双尾),相关性显著。
由输出结果可以看出,相关系数
,P值=0,认为绝对残差值
与自变量
显著相关,故误差项存在异方差性。
2.2.2. 一元加权最小二乘模型的建立
针对上述存在的异方差性问题,我们采用加权的一元最小二乘估计来改善模型。下面我们对公式(3-1)、(3-2)进行一定的变换
(3-4)
(3-5)
其中
,为自变量的加权平均,
为因变量的加权平均,权函数
,m是待定的未知参数。
下面利用SPSS软件进行方程拟合:
① 确定幂指数m的最优值,输出结果如表3:
a. 选择了相应的幂进行进一步分析,这是因为,它使对数似然函数最大化;b. 因变量:GDP,源变量:第一产业。
根据以上的输出结果,幂指数最优的取值为
(3-6)
② 建立模型
根据以上选出的最优幂指数,利用Excel软件,首先计算出不同时间段的权重大小。
之后由公式(3-4)、(3-5),利用SPSS软件计算出加权最小二乘估计的方程系数,输出结果见表4:

Table 4. UNARY weighted least square estimation output
表4. 一元加权最小二乘估计输出结果
a. 因变量:GDP;b. 加权最小平方回归–按权重加权。
根据输出结果可以看出,回归方程显著,回归系数
,且二者均显著,因此加权之后的回归方程为
(3-7)
改进后的回归方程表明,自变量
每增加一个单位,相应的GDP平均增加10.002个单位。
为了更直观地对比加权前与加权后的残差变化,我们以第一产业增加值
为横轴,以权变换残差
为纵轴画残差图见图2:
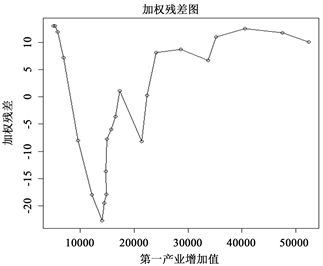
Figure 2. Weighted least square estimation residual diagram
图2. 加权最小二乘估计残差示意图
由图像我们能够看出明显的自相关现象,因此接下来考虑利用迭代的方法消除自相关性,来建立新的一元回归模型。
2.3. 迭代法建立模型
2.3.1. 样本相关系数的计算
利用SPSS软件,计算第一产业增加值与GDP之间的相关性,输出结果见表5:

Table 5. Output table of the correlation coefficient between primary sector of the economy and GDP
表5. 第一产业增加值与GDP的相关系数输出表
**.在0.01级别(双尾),相关性显著。
由输出结果能够看出二者之间存在显著的相关性,相关系数
,非常接近1,因此采用一种特殊的迭代法——差分法,消除残差自相关性。
2.3.2. 利用差分法消除自相关性
首先计算差分
,
。
然后利用SPSS做
对
过原点的最小二乘回归,输出结果见表6:

Table 6. The output of the regression model established by the difference method
表6. 差分法回归模型建立的输出结果
a. 因变量:差分后的GDP;b. 过原点线性回归。
由输出结果可以看出,模型显著,
,因此差分法建立的模型如下
(3-8)
即
(3-9)
3. 多元回归模型的建立
3.1. 多元回归模型的普通最小二乘估计
3.1.1. 回归模型的建立
由相关文献 [4] 我们知道,GDP y的变化不仅由第一产业
影响着,同时还受第二产业
、第三产业
的影响,因此通过查阅相关资料,我们能够获得1990-2012年间GDP以及第一、二、三产业增加值的相关数据。
解释变量有三个,被解释变量有一个,根据多元线性回归的回归系数公式
(4-1)
利用SPSS软件去计算,输出结果见表7:

Table 7. The output of the coefficient calculation of multivariate regression equation
表7. 多元回归方程系数计算输出结果
a. 因变量:GDP。
由输出结果可以看出,常数变量的显著性
远远大于显著性水平
,因此回归方程的拟合效果并不理想。
下面考虑自变量之间的相关性(表8)。

Table 8. Independent variable correlation test output
表8. 自变量相关性检验输出结果
**.在0.01级别(双尾),相关性显著。
由输出结果能够看出,第一产业与第二产业,第二产业与第三产业有着高度的自相关性,因此需要做一定的自变量处理。
3.1.3. 逐步回归法 [5] 选择自变量
取
,
,利用SPSS软件进行运算,输出结果见表9:


Table 9. The result of the stepwise regression
表9. 逐步回归法输出结果
a. 因变量:GDP。
由输出结果可以得出,逐步回归的最优子集模型为y与
、
的模型,即排除掉了第一产业,仅建立GDP与第二产业、第三产业的回归模型,相应的方程为
(4-2)
以上方程表明当固定第三产业
不变,第二产业
每增加一个单位,相应的GDP平均增加1.216个单位。同时若固定第二产业
不变,第三产业
每增加一个单位,相应的GDP平均增加0.976个单位。
3.2. 残差分析
3.2.1. 残差计算与绘图
首先通过Excel软件计算出各时间段的残差值。
利用R软件画出残差值与时间的关系图见图3:
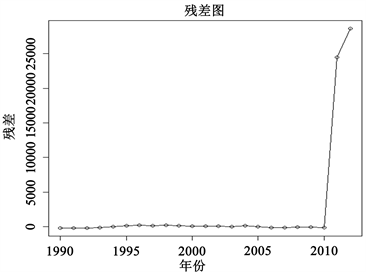
Figure 3. Residuals graph of multiple linear regression
图3. 多元线性回归残差图
由图像能够看出,除了2011、2012年的残差较大之外,其余时间段残差值较平稳,不存在异方差、自相关现象,因此模型较为合理。
4. 评价与总结
本文通过一元最小二乘估计、多元最小二乘估计,分别建立了GDP与第一产业增加值和GDP与第二、三产业增加值之间的回归模型,结果如公式(3-8)、(4-2)。表面上看是两个不同的回归模型,但由于第一产业与第二、三产业之间存在较强的相关关系,即第一产业的变化一定会有相应的第二、三产业的变化,因此实质上本文是通过两种不同的途径来建立了两个相似的回归方程。这便于我们通过今后的产业量来估计我国GDP的增速,从而做出一些相关的政策调整。
参考文献