基于模糊PID的路径跟踪控制系统

Path Tracking Control System Based on Fuzzy PID

摘要: 为提高自动导航插秧机路径跟踪控制系统性能，提出一种基于模糊PID算法调整插秧机前轮转向角度的控制方法。该方法首先建立被控对象的运动学模型，根据运动学模型对模糊PID控制算法进行设计。其次运用Matlab对路径跟踪控制系统进行仿真分析，仿真结果表明：所设计模糊PID控制方法相比于传统PID控制方法，可以有效减少系统的超调量和到达稳态的时间。最后进行动态试验验证，传统PID控制方法下，小车底盘以0.35和0.85 m/s的速度行驶时，最大路径跟踪误差为3.8和6.5 cm，平均路径跟踪误差为2.47和3.67 cm；在模糊PID控制方法下，小车底盘以0.35和0.85 m/s的速度行驶时，最大路径跟踪误差为2.1和4.8 cm，平均路径跟踪误差为1.57和2.7 cm；试验表明：模糊PID控制性能优于传统PID算法，更适合于插秧机路径跟踪控制。

Abstract: In order to improve the performance of the path tracking control system of the automatic naviga-tion transplanter, a control method based on the fuzzy PID algorithm to adjust the steering angle of the front wheel of the transplanter is proposed. Firstly, the kinematic model of the controlled object is established, and the fuzzy PID control algorithm is designed according to the kinematic model. Secondly, Matlab is used to simulate the path tracking control system. The results show that the performance of the fuzzy PID control method is better than the traditional PID control method, which can effectively reduce the overshoot of the system and the time to reach the steady state. Finally, the dynamic test is carried out to verify that under the traditional PID control method, the maximum path tracking error is 3.8 and 6.5 cm, and the average path tracking error is 2.47 and 3.67 cm when the car chassis is running at the speed of 0.35 and 0.85 m/s; under the fuzzy PID control method, the maximum path tracking error is 2.1 and 4.8cm, and the average path tracking error is 1.57 and 2.7 cm when the car chassis is running at the speed of 0.35 and 0.85m/s. The experiment shows that the performance of fuzzy PID control is better than that of traditional PID algorithm, and it is more suitable for path tracking control of transplanter.

1. 引言

自动导航技术符合精准农业对作业机械的要求，能够减小农业生产对劳动力的依赖性，使驾驶人员成为农业机械的管理者，可以大幅度降低驾驶人员的劳动强度，能够保证插秧质量和效率 [1]。路径跟踪是自动导航的核心技术，也是导航控制的重点和难点，路径跟踪控制方法的选择决定了农机自动导航的作业质量和效率 [2]。由于水田的工作环境较为恶劣，插秧机在田间行驶时容易发生颠簸，使插秧机的航向发生变化，因此，提高自动导航插秧机路径跟踪控制系统性能是亟待解决的问题。

国内外许多学者对自动导航的路径跟踪控制技术进行了研究，并取得了相当丰硕的成果，卡耐基梅隆大学的Wallance和Amidi等将纯追踪模型用于汽车的自动导航，实现了路径跟踪控制 [3] [4]；黄沛琛等人把车辆的运动学模型简化为二轮车模型，基于纯追踪模型设计了路径跟踪控制系统 [5]。纯追踪模型的主要调节参数为前视距离 [6]，前视距离的取值是纯追踪模型实现路径跟踪的关键，取值不当会直接影响路径跟踪效果。刘正铎等人基于线性模型预测控制的方法设计了路径跟踪控制系统，并对农用运输车辆路径跟踪控制系统的稳定性进行了分析和优化 [7]。线性模型预测控制要求建立精确的动力学模型或运动学模型 [8]，由于插秧机在田间工作环境恶劣，建立动力学模型或运动学模型难度较大。周建军等人设计了基于模糊控制算法的农用车辆路径跟踪控制系统，并在改装的电瓶车上开发了自动导航控制系统，直线段最大偏差为0.19 m，曲线段最大偏差为0.26 m [9]。模糊控制不需要对被控对象建立精确的数学模型，核心是用所制定的模糊规则来实现对系统的控制，具有较好的适应性，但是模糊控制存在控制精度较低的问题，因此通常与其它算法组合使用 [10]。罗锡文等人设计了基于PID算法的自动转向控制系统，并在东方红拖拉机上进行了田间试验，试验结果表明，在0.8 m/s的行驶速度下，拖拉机的跟踪误差最大不超过15 cm，平均跟踪误差不超过3 cm [11]。PID控制结构简单，适用性强，但是参数调整困难。

为提高自动导航插秧机路径跟踪控制系统的准确性和稳定性，本文设计了一种基于模糊PID算法的路径跟踪控制方法，在PID控制的基础上加入一个模糊调节环节，实现对PID控制参数的在线调整，通过控制插秧机前轮转向角度的变化实现路径跟踪。通过仿真与试验，验证所设计的模糊PID控制方法的性能和适应性。

2. 控制系统总体结构

路径跟踪即通过控制系统调整车辆前进方向，使车辆跟随预定义路线行驶 [12]，当车辆偏离预定义路线时动态调整车辆前轮转角，以保证路径跟随的精度。

插秧机路径跟踪控制原理如图1所示。导航定位系统通过安装在插秧机上的GPS接收机和传感器实时获取插秧机的位置、速度和航向角等运动参数，自动导航系统通过对比预定义路径和当前位置，得到横向偏差和航向角偏差，将两个偏差或偏差变化率作为路径跟踪控制算法的输入，输出插秧机期望前轮转角，转向控制系统将期望前轮转角转换为实际前轮转角，通过控制电动方向盘转动相应的角度来减小偏差，转角传感器实时反馈前轮转角信息给导航定位系统，形成闭环控制实时修正前轮转角，从而实现了自动导航插秧机的路径跟踪。

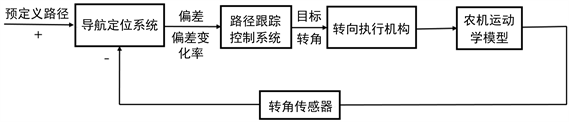
Figure 1. Path tracking control principle

图1. 路径跟踪控制原理

3. 运动学模型

井关公司生产的2Z-6B(PZ60-HGR)型插秧机为前轮转向、四轮驱动。由于插秧机在田间工作时，运行速度较低，动力学对控制系统产生的影响较小，而且建立动力学模型难度较大，所以只对插秧机建立运动学模型即可满足要求。

在运动学分析中，将插秧机视为刚体，假设插秧机运行在平坦地面，且不考虑插秧机出现侧滑、俯仰等运动情况，可以将插秧机简化为二轮车运动模型 [13]。以Y轴为目标路径，Y轴的正方向为目标路径的前进方向，X轴垂直于Y轴方向，取X轴向右为正方向，建立如图2所示的运动学模型。

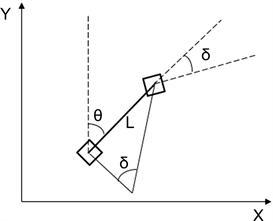
Figure 2. Kinematic model of transplanter

图2. 插秧机运动学模型

该模型以插秧机后轴中心为参考点，对插秧机进行运动学分析可得：

$\{\begin{array}{l}{x}^{\prime }\left(t\right)=v\sin \theta \\ y^{\prime }\left(t\right)=v\cos \theta \\ {\theta }^{\prime }\left(t\right)=\frac{v\tan \delta }{L}\end{array}$ (1)

式中，L：前后轮轴距；

v：插秧机速度；

$\theta$ ：航向角，取逆时针方向为正；

$\delta$ ：前轮转角，取逆时针方向为正。

4. 模糊PID控制系统

4.1. PID控制

PID控制采用比例、积分和微分的方式对系统进行控制。PID控制分为模拟PID控制和数字PID控制两种方式，本研究用离散化的方法对输入信号进行处理，采用数字PID控制方式来实现对系统的控制 [14]。传统PID控制表示方法：

$u\left(t\right)=K_p\left[e\left(t\right)+\frac{1}{T_i}{\displaystyle {\int }_0^{t}e\left(t\right)\text{d}t}+T_d\frac{\text{d}e\left(t\right)}{\text{d}t}\right]$ (2)

式中， $u\left(t\right)$ ：输出信号；

$K_p$ ：比例系数；

$e\left(t\right)$ ：输入信号；

$T_i$ ：积分时间；

$T_d$ ：微分时间。

增量式PID控制的输出是控制量的增量，输出只与前两次的误差有关，不会造成误差累积问题，控制系统具有较好的稳定性，适用于带积分项的控制系统，故本文采用增量式PID控制。增量式PID控制表示方法：

$\Delta u\left(k\right)=k_p\left(e\left(k\right)-e\left(k-1\right)\right)+k_{i}e\left(k\right)+k_d\left(e\left(k\right)-2e\left(k-1\right)+e\left(k-2\right)\right)$ (3)

式中， $\Delta u\left(k\right)$ ：控制输出增量；

$e\left(k\right)$ ：输入偏差；

$e\left(k-1\right)$ ：上一次输入偏差；

$e\left(k-2\right)$ ：上两次输入偏差。

4.2. PID控制的参数整定

由于插秧机在田间工作环境恶劣，精确的数学模型建立难度较大，故采用临界比例度法对系统进行参数整定 [15]。

首先，把PID控制设置为K_p值较小的纯比例调节，然后将K_p值逐渐增大，取系统出现振荡时的K_p值为K_pcnt，取振荡的两个波峰之间的时间为T_n，根据表1所示规则计算PID控制K_p、K_i和K_d三个参数的值。

Table 1. Adjustment rules of critical scale method parameters

表1. 临界比例度法参数调整规则

4.3. 模糊PID控制设计

自动导航插秧机路径跟踪控制系统是一种典型的非线性系统。为了解决传统PID控制精度不足的问题，在PID控制的基础上加入一个模糊调节环节，从而形成模糊PID控制，实现对PID控制参数的在线调整。模糊PID控制具有精度高、适应性强的优点。

模糊控制的本质是用所制定的模糊规则来实现对系统的控制。首先需要对输入的信号进行模糊化处理。然后，根据设定的模糊推理规则得到模糊输出信号。最后，对模糊输出信号进行清晰化处理得到确定的控制量，并将确定的控制量输出到执行机构，从而实现对系统的控制。本文选择两输入、三输出的模糊逻辑控制结构，其中，模糊输入为插秧机横向偏差e和偏差变化率ec，模糊输出为∆K_p、∆K_i和∆K_d，对PID控制参数进行实时调整，从而实现自动导航插秧机的路径跟踪控制。调整规则为：

$K_p=K_{p1}+\Delta K_p$ (4)

$K_i=K_{i1}+\Delta K_i$ (5)

$K_d=K_{d1}+\Delta K_d$ (6)

式中，K_p1、K_i1和K_d1为PID控制的初始参数值，K_p、K_i和K_d为调整后的参数值。

模糊PID系统结构如图3所示，

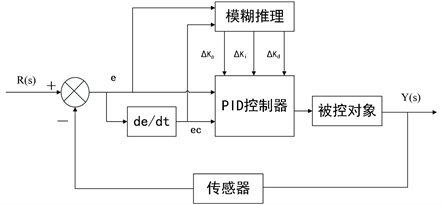
Figure 3. Structure of fuzzy PID system

图3. 模糊PID系统结构图

1) 输入、输出变量的模糊化

模糊子集的输入输出变量一般采用“大、中、小”的方式描述。大多数控制系统选择7个语言变量，也可依据不同的系统控制要求来增加或减少变量。语言变量的多少对控制效果有一定的影响，若变量选择过少，控制系统的精度得不到保障，达不到理想的控制效果；若变量选择过多，变量划分的精确度得到提高，但是会增大系统的计算量和设计难度。

本文选用7个语言变量来对插秧机路径跟踪控制系统进行描述，系统论域设计如下：

a) 横向偏差e

基本论域为：[−12，12]；

量化论域为：{−6，−5，−4，−3，−2，−1，0，1，2，3，4，5，6}；

量化因子：12/6 = 2。

b) 偏差变化率ec

基本论域为：[−6，6]；

量化论域为：{−6，−5，−4，−3，−2，−1，0，1，2，3，4，5，6}；

量化因子：6/6 = 1。

c) 比例系数∆K_p

基本论域为：[−8，8]；

量化论域为：{−3，−2，−1，0，1，2，3}；

量化因子：3/8=0.375。

d) 积分系数∆K_i

基本论域为：[−6，6]；

量化论域为：{−3，−2，−1，0，1，2，3}；

量化因子：3/6=0.5。

e) 微分系数∆K_d

基本论域为：[−6，6]；

量化论域为：{−3，−2，−1，0，1，2，3}；

量化因子：3/6 = 0.5。

2) 定义输入和输出隶属度函数

本研究对模糊控制的输入和输出变量均采用三角形隶属度函数，输入和输出变量对应的隶属度函数如图4和图5所示。

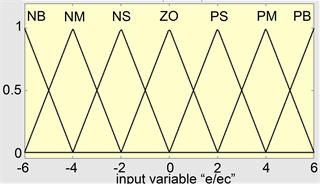
Figure 4. Membership function of input variables e and ec

图4. 输入变量e、ec隶属度函数

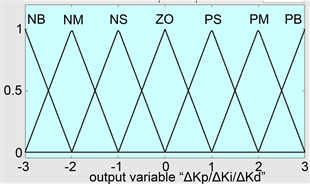
Figure 5. Membership function of ∆K_p, ∆K_i, ∆K_d output variables

图5. 输出变量∆K_p、∆K_i、∆K_d的隶属度函数

3) 建立模糊控制规则

模糊PID控制的主要目的是确定K_p、K_i、K_d三个参数的相互影响，以及三个参数与横向偏差e和偏差变化率ec之间的模糊关系。模糊PID控制器的输入为插秧机横向偏差e和偏差变化率ec，模糊控制的输出为∆K_p、∆K_i、∆K_d，输出的∆K_p、∆K_i和∆K_d对PID控制部分的K_p、K_i和K_d三个参数进行实时调整，以保证插秧机路径跟踪控制系统具有较好的稳定性。

模糊控制规则的设计原则：

a) 横向偏差e和偏差变化率ec的正负表示方向，当横向偏差e的绝对值较大时，系统应快速减小横向偏差e，为提高系统的反应速率，应设置较大的K_p值；提高系统的反应速率会产生微分溢出，为防止微分溢出，应设置较小的K_d值；同时为防止出现积分饱和现象，应设置K_i的值为0。

b) 当横向偏差e的绝对值较小时，为保证系统稳定性良好，K_p值和K_i值应取较大的值；同时为增强路径跟踪控制系统的抗干扰能力，应该选取适当的K_d值，K_d值的具体调整原则：当偏差变化率ec的绝对值较小时，K_d值应取较大值，当偏差变化率ec的绝对值较大时，K_d值应取较小值。

根据上述模糊控制规则，设计系统模糊控制规则如表2~4所示。

Table 2. Kp fuzzy control rules

表2. K_p模糊控制规则表

Table 3. Ki fuzzy control rules

表3. K_i模糊控制规则表

Table 4. Kd fuzzy control rules

表4. K_d模糊控制规则表

模糊控制部分的输出变量∆K_p、∆K_i、∆K_d输出曲面分别如图6~8所示。图中X轴代表横向偏差e，Y轴代表偏差变化率ec，Z轴分别代表∆K_p、∆K_i、∆K_d三个输出变量。

Figure 6. ∆K_p output surface

图6. ∆K_p输出曲面

Figure 7. ∆K_i output surface

图7. ∆K_i输出曲面

Figure 8. ∆K_d output surface

图8. ∆K_d输出曲面

4) 模糊推理和反模糊化

模糊推理的过程在模糊逻辑工具箱中进行，设置模糊逻辑推理类型为Mamdani型，模糊逻辑推理的各参数设置如表5所示。

Table 5. Fuzzy logic reasoning parameter setting

表5. 模糊逻辑推理参数设置

经过模糊推理得到的∆K_p、∆K_i、∆K_d是模糊集合，不能直接用于控制对象，需要把输出量的模糊集合转化为确定的控制量，即对模糊集合进行清晰化处理。目前主要有三种常用的清晰化方法：最大隶属度法、重心法和加权平均法，其中最大隶属度法适用于计算简便控制精度要求不高的情况，重心法的输出较为平滑，加权平均法在工业应用中较为广泛。本文采用重心法对模糊集合进行清晰化处理，具体方法：首先，找到输出隶属度函数曲线与坐标轴的横轴所围成面积的重心。然后，将这个重心作为输出变量的代表点，对输出范围内几个连续点的重心进行计算即可。

重心法即

$u=\frac{{\displaystyle \int u\ast {\mu }_N\left(u\right)\text{d}u}}{{\displaystyle \int {\mu }_N\left(U\right)\text{d}u}}$ (7)

当模糊控制的输出变量为离散集时，则有

$u=\frac{{\displaystyle \sum u_i\ast {\mu }_N\left(u_i\right)}}{{\displaystyle \sum {\mu }_N\left(u_i\right)}}$ (8)

5. 系统仿真与试验验证

5.1. 仿真分析

使用Simulink分别建立基于PID算法和模糊PID算法的自动导航插秧机路径跟踪控制系统模型，为对比两种控制方法的性能，对系统进行仿真。

在两个控制系统中分别输入单位阶跃信号进行仿真，系统的响应曲线如图9所示，图中蓝色曲线为PID控制下系统的响应曲线；绿色曲线为模糊PID控制下系统的响应曲线。

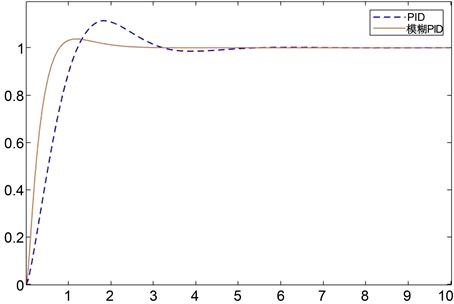
Figure 9. Simulation response curve of control system

图9. 控制系统仿真响应曲线

从图中可以看出，在PID控制方法下，响应曲线上升时间为1.9 s，最大超调量为10%，调节时间为4.7 s；在模糊PID控制方法下，响应曲线上升时间为1.2 s，最大超调量为5%，调节时间为2.1 s。相比于PID控制，模糊PID控制方法下系统的超调量减小，响应时间加快，系统的动态性能有所提高。

5.2. 动态试验验证

为验证所述模糊PID控制方法的路径跟踪性能，将PID控制程序和模糊PID控制程序植入单片机中，分别用PID和模糊PID控制小车底盘进行路径跟踪。小车底盘主要参数如表6所示。

Table 6. Main parameters of trolley chassis

表6. 小车底盘主要参数表

设置小车底盘在低速(0.35 m/s)和高速(0.85 m/s)两种状态下行驶。PID控制方法下路径跟踪误差结果统计如图10所示，路径跟踪最大误差出现在转弯处。

从图10中可以看出，当小车底盘分别以0.35和0.85 m/s速度行驶时，最大路径跟踪误差分别为3.8和6.5 cm，平均路径跟踪误差分别为2.47和3.67 cm。

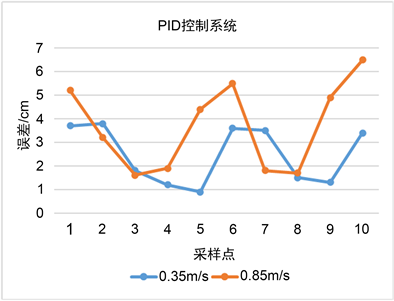
Figure 10. Error statistics under PID control method

图10. PID控制方法下误差统计

模糊PID控制方法下路径跟踪误差结果统计如图11所示，路径跟踪最大误差出现在转弯处。

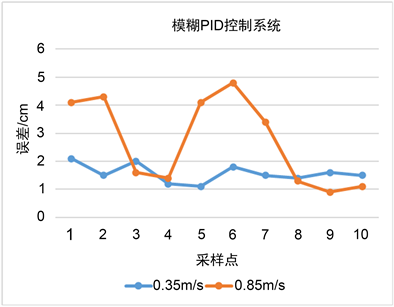
Figure 11. Error statistics under Fuzzy PID control method

图11. 模糊PID控制方法下误差统计

从图11中可以看出，当小车底盘分别以0.35和0.85 m/s速度行驶时，最大路径跟踪误差分别为2.1和4.8 cm，平均路径跟踪误差分别为1.57和2.7 cm。动态试验结果表明在高速和低速两种行驶状态下，模糊PID控制方法的最大路径误差与平均路径误差均小于PID控制方法下的路径跟踪误差。验证了所提出的模糊PID控制方法较传统PID控制方法具有更好的控制性能。

6. 结论

1) 提出一种基于模糊PID控制算法的自动导航插秧机路径跟踪控制方法。该模糊PID控制相比于传统PID控制算法可减小调整超调量，减少响应时间，可提高系统动态性能。

2) 通过试验验证表明，在模糊PID控制方法下，当小车底盘以0.35和0.85 m/s的速度行驶时，最大路径跟踪误差为2.1和4.8 cm，平均路径跟踪误差为1.57和2.7 cm。验证了模糊PID控制方法性能更优，且对低速和高速都具有适应性。

致谢

本论文的顺利完成，离不开各位老师、同学和朋友的关心和帮助。在此感谢刘双喜老师、王玉亮老师的支持；感谢实验室李玉风，宋悦，权泽堃等同学的帮助。

基金项目

本研究得到山东现代农业产业技术体系水稻创新团队资助项目；“双一流”奖补资金项目(SYL2017XTTD14)；山东省重点研发计划(2017GNC12109)支持。